大纯滞后对象多变量系统的改进ERGA配对方法

张雨飞 陈 霈 苏志刚 贺华杰 吕剑虹

(东南大学能源热转换及其过程测控教育部重点实验室，南京210096)

(东南大学能源与环境学院，南京210096)

大型复杂的工业过程通常是多输入多输出(MIMO)系统，MIMO系统由于各个输入-输出量间存在相互影响而十分复杂.解决多变量控制的方法有多种，其中分散策略在实际工业应用中占有主要地位.分散策略是将MIMO系统分解成多个SISO回路，然后采用PID控制器对每个单回路进行控制，其中如何进行变量配对是处理多变量系统的关键技术.由于各变量之间存在关联作用，如何评价输入-输出量之间的关联程度，并以此获得配对规则，达到最佳的控制效果，是分散策略设计的困难所在.

在多变量配对中，应用最广泛的配对规则是Bristol提出的静态相对增益矩阵(RGA)［1］，只需要开环系统的稳态增益即可获得相应的配对规则，并且计算简便.但是，RGA只利用了稳态增益而没考虑过程的动态特性，因此，有时所得到的配对是不合理的.在此基础上，人们提出了不少改进的动态配对方法，如Witcher等［2］提出了动态相对增益矩阵(DRGA)，采用带拉普拉斯算子的传递函数模型替代RGA计算中的稳态模型;2003年Mc Avoy等［3］又对DRGA进行了新的定义，提出了比较完善的回路配对准则;Gagnepain等［4］提出了平均相对增益矩阵(ARGA)的定义，采用基于开环阶跃响应所得到的某个时间段的平均动态增益，来替代RGA中的静态增益进行计算，从而得到多回路系统的配对原则;Zhu［5］提出了相对关联矩阵(RIA)的定义，将输入量u对输出量y的作用分为直接作用和在关联存在的情况下其他输入对y的影响两类，并将两者的相对值定义为相对关联度，以此建立相对关联矩阵进行计算;Kookos等［6］采用RGA和RIA对高维数系统的动态优化进行了研究;叶凌箭等［7］提出将相对关联阵列(RIA)与ARGA相结合形成平均相对增益矩阵(ARIA)，将被控量对受控制量的影响程度视为一种能量传输，以平均能量衡量关联程度;Xiong等［8］提出了效能相对增益矩阵(ERGA)的定义，使用传递函数的带宽矩阵对静态增益矩阵进行修正，这样可以综合反映对象动态和静态特性;Xiong等［9］又于2006年提出对于有纯滞后的被控对象，在使用ERGA进行变量配对时，为了体现纯滞后对系统动态特性的影响，采用截止频率代替带宽进行计算的ERGA配对方法.对于带纯滞后的对象，ERGA使用静态增益和过程传递函数中的截止频率，对回路的关联进行了更全面的描述.但是，截止频率的计算比较麻烦，尤其是大纯滞后环节，使用波特图计算截止频率比较困难，并且不利于工程人员的理解.

本文在ERGA的基础上，采用纯滞后矩阵对带宽矩阵进行加权以替代截止频率阵，用加权后的矩阵进行配对计算，使ERGA规则能适用于带纯滞后的对象，得到了改进的ERGA配对方法.通过仿真实例与RGA，ERGA及其他动态配对法进行比较，证实了改进ERGA的有效性和合理性.

1 RGA以及ERGA

控制回路的配对决定了系统的结构，最常用的回路配对方法是以 RGA［1］和 NI［10］为基础的配对规则.

1.1 RGA 配对规则

Bristol［1］给出了RGA配对规则的计算方法.首先，定义相对增益为

式中，分子为除uj外其他输入量u都保持恒定，即所有其他回路都开环时，uj对yi的增益;分母为除yi外其他输出量y都保持恒定，即其他回路都闭合时，uj对yi的增益;C为常数.

用这些相对增益组成n×n的相对增益矩阵，即

Λ矩阵可由开环增益直接计算得到，即

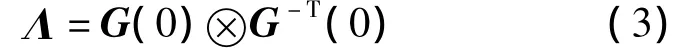
式中，运算符⊗是Hadamard乘积，即点对点相乘;G(0)为稳态增益矩阵.

RGA的配对规则是:

1)配对的RGA元素尽量趋近于1.0;

2)所有配对的RGA元素都应为正;

3)尽量避免很大的RGA元素.

此外，当回路都闭合时，多回路系统的稳定性可以由NI值［10］的正负来进行判断，即

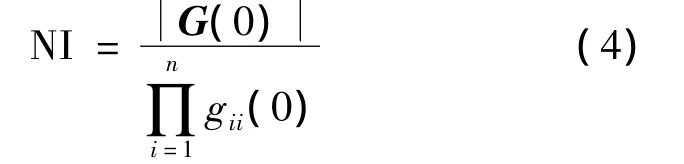
1.2 ERGA 配对规则

Xiong 等［8-9，11］提出了 ERGA 的定义和计算方法，在RGA的基础上引入临界频率对静态增益进行修正，从而得到效能增益.

对于不带纯滞后的对象，临界频率等于带宽，即在频率特性曲线上输出为时的频率值，即

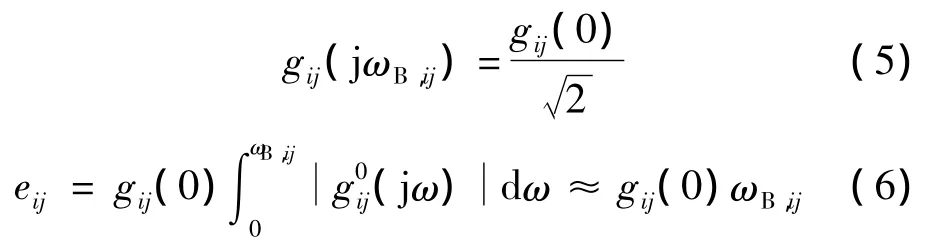
式中，ωB，ij为传递函数的带宽;eij为效能增益;i，j=1，2，…，n.

对于带纯滞后的对象，应用截止频率ωu，ij代替 ωB，ij进行计算.截止频率 ωu，ij是指传递函数的波特图中，使得相位为－π时的频率，即

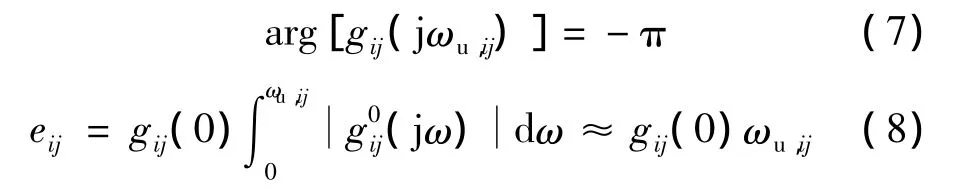
当对象无纯滞后时，ωa，ij= ωB，ij;当对象有纯滞后时，ωa，ij= ωu，ij.因此可以得到临界频率矩阵 Ω和效能增益矩阵E为

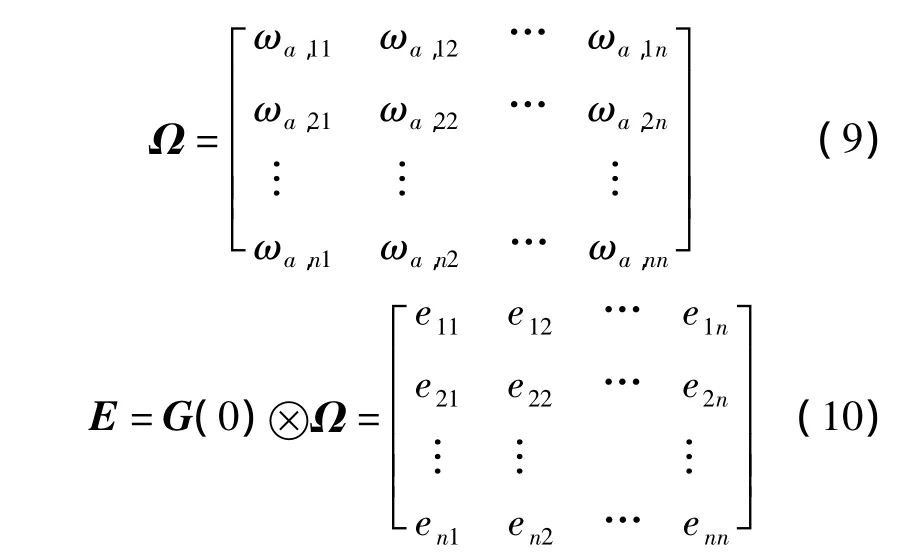
当回路yi－uj闭合时，由于对其他回路而言，eij是能量关联尺度，因此其值越大，则该回路配对的优势也越大.用效能增益矩阵E代替稳态增益矩阵G(0)，代入RGA规则中计算，得到反映输出变量yi和输入变量uj之间的效能相对增益φij为

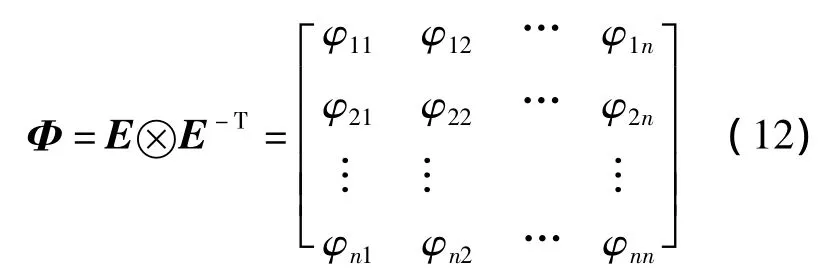
类似于RGA，ERGA配对规则为:

1)配对的ERGA元素尽量趋近于1.0;

2)所有配对的ERGA元素都应为正;

3)尽量避免很大的ERGA元素;

4)NI值为正.

1.3 RGA与ERGA的比较

由于RGA只利用了稳态增益的信息，而不能反映系统的动态特性，使得在某些情况下RGA会给出错误的配对信息;ERGA由于引入了临界频率来反映系统的动态特性，因此具有比RGA更好的动态适用性.以下例子给出对比结果.

算例1RGA与ERGA配对结果比较

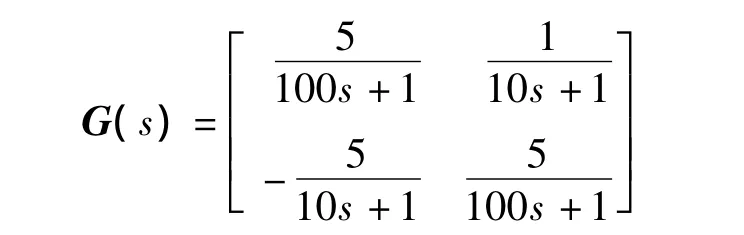
采用RGA规则计算得

因此，RGA的计算结果为对角匹配，即 u1→y1，u2→y2.

由此得到 φ12=φ21=0.952 4.所以 ERGA 的计算结果为非对角匹配，即 u1→y2，u2→y1.实际上，可以看出，非对角元素的时间常数远小于对角元素的时间常数，所以在动态过程中非对角对象响应速度明显快于对角对象，因此，采用非对角匹配更加合理.

由算例1可以看出，由于稳态相对增益阵列RGA只考虑了稳态影响的大小，没有考虑动态特性，得出的配对无法反映对象的动态特性，导致在动态响应过程中不能达到最佳的效果.而效能相对增益阵列ERGA用临界频率矩阵对静态增益矩阵进行加权，将对象的时间常数以临界频率的形式体现出来，在一定程度上反映了对象的动态特性，因此ERGA配对规则所得到的结果更好.

2 改进ERGA配对规则

对象的动态特性不仅反映在时间常数上，也反映在纯滞后时间τ上，对于不带纯滞后的环节，ERGA将带宽矩阵和静态增益矩阵相结合就能较好地反映静、动态响应效果;而对于带纯滞后的环节，ERGA则采用截止频率来代替带宽，这样虽然在一定程度上体现了对象的纯迟延特性，但是截止频率体现的是对象纯滞后时间绝对值的大小，对于滞后时间绝对值较小，但是与时间常数Tc的相对值较大的对象，特别是大纯滞后对象(τ/Tc＞0.5)，用截止频率来计算得到的结果可能是错误的.同时，在计算截止频率时要使用波特图，不利于计算和理解.

对于大纯滞后对象过程，往往采用纯滞后时间τ与时间常数Tc的相对值τ/Tc来反映滞后作用对动态过程的影响，因此，本文提出用τ/Tc作为参数，形成纯滞后矩阵T，用T来修正带宽矩阵Ω，从而得到修正后的矩阵Ω'，这样就综合考虑了对象的时延特性，能更加全面地衡量系统的动态特性.纯滞后矩阵T的表达式为

式中，τij，Tc，ij，i，j=1，2，…，n 分别为纯滞后时间和时间常数.

当 τ=0 时，e－τ/Tc=1，Tij=1，即当无纯滞后时，对原 Ω 无影响;当 τ＞0 时，τ越大，e－τ/Tc越小，修正后使得原Ω的元素变小，即当纯滞后相对较大时，使得配对的可能性大大降低.

由于是采用相对值τ/Tc作为衡量纯迟延的参数，即使τ值稍大，如果Tc值较大，则τ/Tc相对较小，e－τ/Tc≈1，使得原 Ω 的元素变化很小，此时由于对象的带宽本身较小，而纯滞后的影响不明显，故用带宽来反映对象的动态特性可以认为是正确的.

当 τ较大，而 Tc较小时，e－τ/Tc较小，修正后使得Ω减小，此时由于纯滞后相对较大，在配对时必须考虑纯滞后的影响，所以应该用e－τ/Tc来修正带宽，才能正确地反映出对象的动态特性.

改进ERGA的计算步骤如下:

①计算过程的稳态增益矩阵G(0).

②计算过程的带宽矩阵Ω.

③ 使用τ/Tc计算出纯滞后矩阵T.

④ 用Ω⊗T修正，得到带宽矩阵Ω'.

⑤用Ω'⊗G(0)修正，得到改进效能增益矩阵E.

⑥ 用E⊗E－T修正，得到改进的相对效能矩阵Φ，并且用Φ来指导配对.

结合NI条件，使用改进ERGA进行配对的规则如下:

1)配对后的改进ERGA元素应尽可能接近1;

2)所有配对的改进ERGA元素应大于0;

3)尽量避免改进ERGA元素的配对;

4)NI＞0.

对改进ERGA和ERGA进行比较，来验证改进ERGA的正确性和方便性.

算例2ERGA与改进ERGA配对比较

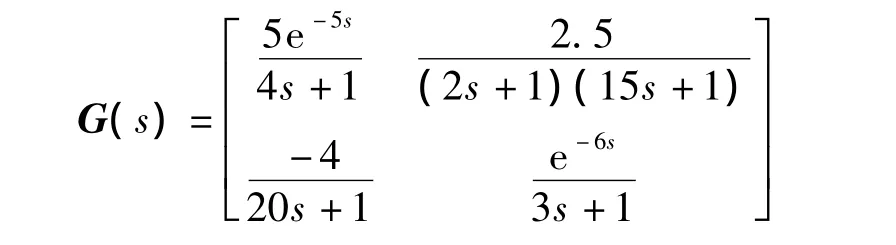
用ERGA进行计算时，由于主对角线上的对象有纯滞后，而非对角的对象没有，所以主对角的临界频率采用截止频率，而非对角采用带宽，有

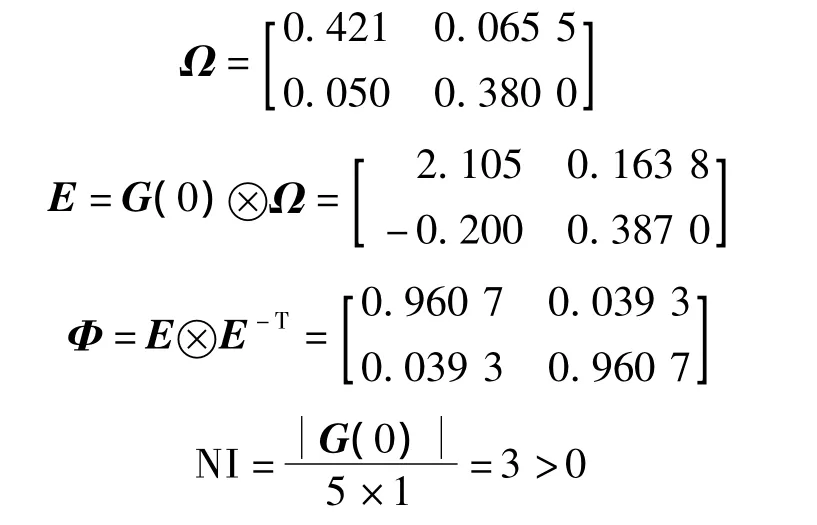
因此，用ERGA配对的结果为对角匹配，即u1→y1，u2→y2.

用改进的ERGA进行计算:

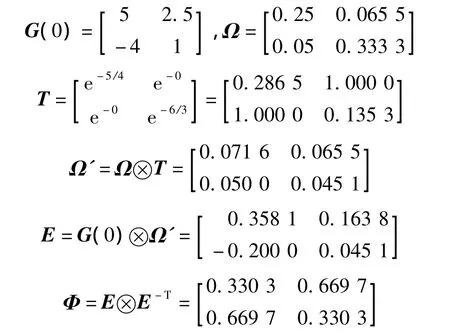
由于主对角元素上含有纯滞后，使用改进ERGA运算时，通过纯滞后矩阵的修正作用，降低了带纯滞后元素配对的可能.所以，用改进ERGA计算的结果应该是非对角匹配，即u1→y2，u2→y1.

实际上，由于对角对象有纯滞后，ERGA的配对结果不合理，而非对角配对更合理.对两者进行仿真验证，结果如图1所示.

由图1中可以看出，采用对角匹配和非对角匹配都可以得到较好的控制效果，但是与对角匹配相比，非对角匹配的过渡过程时间明显短于对角匹配，这说明采用非对角匹配，控制量对被控对象的控制作用更及时，并且采用非对角匹配所得到的响应曲线的超调量总体上优于对角匹配，用非对角匹配的控制结果更佳.因此，采用纯滞后矩阵T和带宽矩阵Ω相结合的改进ERGA规则更能反映出对象的动态特性，得到的配对结果也更合理.

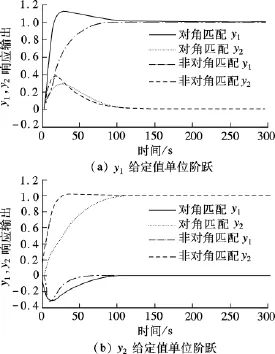
图1 y1，y2响应输出曲线

算例33×3精馏塔的改进ERGA配对计算［7，12-13］

式中，T为塔板温度;P为塔压;L为回流釜液位;QB为再沸器热载荷;D为塔顶馏出量;R为回流比.

根据改进ERGA规则计算得到

由计算结果可看出，可选的配对方案有2个:u1→y1，u2→y3，u3→y2，或者 u1→y1，u2→y2，u3→y3.即 QB→T，D→L，R→P，或者 QB→T，D→P，R→L.采用第1种配对的效果会更好，这与文献［7，12］得到的结论相同.

根据ERGA规则进行计算得

因此得到的配对结果为 u1→y1，u2→y2，u3→y3，即QB→T，D→P，R→L，所得到的结果与文献［7，12］不一致.

通过算例2和算例3可以看出，对于大纯滞后对象，改进ERGA使用纯滞后矩阵T对带宽矩阵进行修正，能更全面地反映对象的动态特性，所得到的配对结果也更加合理.

算例4300 MW流化床锅炉燃烧对象的改进ERGA 配对计算［14］

式中，Tb为床温;Pb为床压，P0为主蒸汽压力;μv为回料阀开度;F1为一次风量;B为燃料量.

根据ERGA规则进行计算得

因此配对的结果为 u1→y1，u2→y2，u3→y3，即 μv→Tb，F1→Pb，B→P0.

按改进ERGA规则进行计算，由于

因此

可以看出，采用改进ERGA规则的配对结果与 ERGA 的结果相同，即 μv→Tb，F1→Pb，B→P0.但是ERGA要使用波特图计算每一个截止频率，而采用改进的ERGA计算时则方便得多，并且容易使工程人员理解和应用.

用Matlab进行仿真，仿真系统结构图及响应曲线如图2所示.从仿真曲线可以看出，除床温Pb由于其本身惯性很大，响应曲线变化较缓慢外，另外2个被控对象都能很好地受到控制.实际上，在电厂的运行中也使用同样的控制方案，即用冷渣器转速μv控制床温Tb，一次风量F1控制床压Pb，给煤量B控制主蒸汽压力P0.所以，采用改进ERGA得到的配对信息是正确的.

图2 床温、床压和主蒸汽压给定值阶跃扰动输出曲线

3 结语

通过4个算例和仿真验证可以看出，采用改进ERGA规则对多输入多输出的工业过程进行配对，能结合稳态增益和对象动态特性，得到最好的配对方案.特别是对于大纯滞后对象，能全面考虑对象的动态特性，防止用ERGA配对时由于动态特性反映不全面，而得到错误的配对结果.改进ERGA配对规则在带纯滞后对象的MIMO系统(如电厂)的变量配对领域有着广阔的应用前景.

References)

［1］Bristol E H.On a new measure of interactions for multivariable process control［J］.IEEE Trans on Automatica Control，1966，11(1):133-134.

［2］Witcher M F，Mc Avoy T J.Interacting control systems:steady state and dynamic measurement of interaction［J］.ISA Transactions，1977，16(3):35-41.

［3］Mc Avoy Thomas，Arkun Yaman，Chen Rong，et al.A new approach to defining a dynamic relative gain［J］.Control Engineering Practice，2003，11(8):907-914.

［4］Gagnepain J P，Seborg D E.Analysis of process interactions with applications to multiloop control system design［J］.Industrial and Engineering Chemistry，Process Design and Development，1982，21(1):5-11.

［5］Zhu Z X.Variable pairing selection based on individual and overall interaction measures［J］.Industrial and Engineering Chemistry Research，1996，35(11):4091-4099.

［6］Kookos I K，Lygeros A I.An algorithmic method for control structure selection based on the RGA and RIA interaction measures［J］.Chemical Engineering Research and Design，1998，76(4):458-464.

［7］叶凌箭，宋执环.多变量控制系统的一种变量配对方法［J］.控制与决策，2009，24(12):1795-1800.Ye Lingjian，Song Zhihuan.Variable pairing method for multivariable control systems［J］.Control and Decision，2009，24(12):1795-1800.(in Chinese)

［8］Xiong Qiang，Cai Wenjian，He Maojun.A practical loop pairing criterion for multivariable processes［J］.Journal of Process Control，2005，15(7):741-747.

［9］Xiong Qiang，Cai Wenjian，He Maojun，et al.Decentralized control system design for multivariable processes—a novel method based on effective relative gain array［J］.Industrial and Engineering Chemistry，2006，45(8):2769-2776.

［10］Niederlinski A.A heuristic approach to the design of linear multivariable interacting subsystems［J］.Automatica，1971，7(6):691-701.

［11］Xiong Qiang，Cai Wenjian.Effective tranfer function method for decentralized control system design of multi-input multi-output processes［J］.Journal of Process Control，2006，16(8):773-784.

［12］Bao J，Chen K H，Zhang W Z，et al.An experimental pairing method for multi-loop control based on passivity［J］.Journal of Process Control，2007，17(10):1101-1110.

［13］叶琼瑜.化工过程多变量系统的PID控制研究［D］.北京:北京化工大学信息科学与技术学院，2008.

［14］郝勇生.大型循环流化床锅炉建模和先进控制方法研究［D］.南京:东南大学能源与环境学院，2009.