一种多策略要素的数据访问调度算法

冯 径 徐 攀 王锦洲 黄 伟

(解放军理工大学气象学院，南京211101)

我国的气象水文数据库分别部署在中央、流域、省级等水利部门，具有分布式特点，通常可抽象为三级节点.就实时水雨情而言，一级节点主要存储国家级测站的数据信息，二级节点用于存储流域内国家和地方测站数据信息，三级节点仅存储本区域内的测站陆地水文数据信息.因此，在设计大量用户并发的透明数据访问服务时，会遇到多个服务器拥有相同数据或在同一服务器中访问不同数据的情况，此时不仅需要满足高优先级任务，更应当考虑公平性.在单纯考虑优先级的调度系统中，特别是当系统负荷较高时，低优先级队列的平均等待时间趋于无限大，必然造成这部分任务由于超过任务时限而被抛弃的结果［1］.因此，在研究数据访问调度算法时，除了考虑传统的截止时间、优先级等任务调度约束条件外，还应根据应用场景，考虑公平性、数据映射代价、安全性、负荷均衡等其他策略要素.

本文以我国的陆地水文分布式数据库系统为背景，针对各类应用对不同区域的数据共享问题，综合考虑多种策略要素，设计了一种多策略要素的调度算法(multi-policy elementsscheduling，MPES).该算法对分布式数据库访问任务进行调度，对不同优先级任务设置不同的调度窗口.在保证安全的基础上，将n个相互独立的任务分配到m个可用的资源节点上，使得总服务时间最小且资源得到充分利用.

1 预备定义

MPES算法由调度预处理等待、调度窗口计算、安全级别映射、节点数据映射、节点分配和非正常状态的判断与处理等6部分组成.在保证安全的基础上，将n个相互独立的任务分配到m个可用的资源节点上.

定义1任务集合 J={ω1，ω2，…，ωn}，其中ωi∈J 为一个多元组，且 ωi=(ci，sei，tyi，pri，di，eti，hi)，ci为任务分配的节点，sei为任务的安全级别要求，tyi为任务请求的数据内容，pri为任务的优先级，di为任务截止时间相对值，eti为任务的执行时间，hi为任务循环跳数(初始值为0).其中，sei，tyi，pri，di，eti已知，且 eti={ti1，ti2，…，tim}为多元组，tim为不同任务在不同节点上的执行时间.

定义2节点可以被描述为一个集合C={c1，c2，…，cm}，其中 m≥2;ci∈C 为一个多元组，且 ci={pei，sei，tyi，li}，pei，sei，tyi和 li分别为节点的性能参数、安全级别、数据内容和最大可连接访问任务数.其中sei和tyi均已知，且tyi为一个集合.

定义3等待调度队列集合 Qw={q1，q2，q3}，其中q1，q2和q3分别为高优先级队列、中等优先级队列和普通优先级队列，且 q1={ω11，ω12，…，ω1x}，q2={ω21，ω22，…，ω2y}，q3={ω31，ω32，…，ω3z}.

根据上述定义，设 Q={ω1，ω2，…，ωl}为当前需要进行调度的任务集合，Qe={ω'1，ω'2，…，ω'k}为当前正在执行的任务集合.

不失一般性，设置3个优先级，即当pri=1，2，3时分别代表高优先级、中等优先级和普通优先级.

2 算法设计

2.1 等待调度预处理

根据任务优先级的不同可将等待调度队列分为不同的优先级队列.本文设计了3种优先级队列q1，q2和q3.预处理的工作主要包含以下内容:①对到来的任务根据优先级不同进行队列分配，同一优先级的任务分配给同一队列;②在每个队列中，采用最小松弛度优先调度(modified least laxity first，MLLF)策略决定任务进入调度窗口的先后次序.

MLLF策略以任务的松弛度Li为任务的优先级，且 Li=di(t)-t-ei(t)=Di-Ci.其中，Di=di(t)-t为任务调度优先级，di(t)为任务的时限，t为当前时间;Ci=ei(t)为任务的运行时间.松弛度Li的值越小，任务的优先级越高;反之则越低.具有最小Li值的任务最先执行［2］.

设 q1的排序结果为 ω11，ω12，ω13，ω14，…;q2的排序结果为 ω21，ω22，ω23，ω24，…;q3的排序结果为 ω31，ω32，ω33，ω34，….

2.2 调度窗口计算

调度窗口可理解为允许某类任务被分配的时间，以一个标准时间T为单位.等待调度任务经过等待调度预处理后，进入不同的优先级队列，然后进行内部排序.标准时间值T以q3中首要任务的期望执行时间为参考.

定义4任务ωi的期望执行时间Ti为该任务在所有节点上的预期执行时间的平均值，即

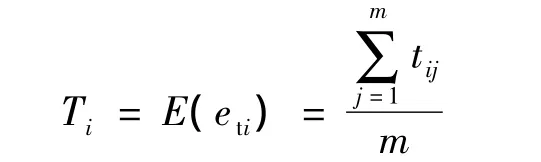
在同时考虑队列公平和队列优先级的情况下，计算得调度窗口W约为6T.根据优先级对每个队列分配不同的调度窗口时间:普通优先级队列的窗口W3≈T;中等优先级队列的窗口W2≈2T;高优先级队列的窗口W1≈3T.

对于普通优先级队列q3，能够进入调度窗口的任务共l3个，满足条件，即

对于中等优先级队列q2，进入调度窗口的任务共 l2个，满足条件，即由此可知，前l2－1个任务的期望执行时间之和小于2T，而 l2个任务的期望执行时间之和大于等于2T.

对于高优先级队列q1，进入调度窗口的任务共l1个，满足条件即由此可知，前l1－1个任务的期望执行时间之和小于3T，而 l1个任务的期望执行时间之和大于等于3T.

图1为调度窗口示例，以每个任务的长度代表该任务的期望执行时间.由图可知，对于普通优先级队列q3，进入调度窗口的元素为ω31;对于中等优先级队列q2，进入调度窗口的任务共5个，分别为 ω21，ω22，ω23，ω24，ω25;对于高优先级队列 q1，进入调度窗口的元素共 6 个，分别为 ω11，ω12，ω13，ω14，ω15，ω16.

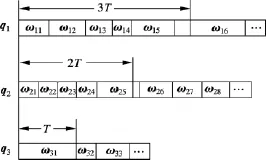
图1 调度窗口示例

2.3 安全级别映射

假设3种安全级别:sei=1表示高安全级别;sei=2表示中等安全级别;sei=3表示低安全级别.

安全级别映射是指对于调度队列内的任务而言，根据任务的安全级别条件，在全局的资源节点内确定能够执行该任务的节点子集.在本算法中，只允许该任务在安全级别高于或等于任务安全级别的节点上执行.

2.4 节点数据映射

若以三级节点的存储内容为一个单元数据，则可将整个系统中每个节点的数据内容ty表示如下:① 对于三级节点ci而言，数据内容为si，即tyi={si};② 对于二级节点ck而言，若该节点包含三级节点 ch，ci，cj的数据，则其数据内容为 tyk={sh，si，sj};③对于一级节点而言，其数据内容为系统内所有单元数据的集合.

数据内容映射需要在安全级别映射已经确定的节点子集内进行，根据任务要求访问的内容来对节点子集进行匹配，查找适合的节点以完成任务.当数据内容映射的集合为空集时，处理同2.3节.

2.5 节点分配

节点分配要综合考虑节点性能和实时负荷.节点性能表示该节点执行任务速度的快慢.采用比值法为每一个节点确定性能参数，以避免需要根据节点CPU型号、数量、内存、存储方式等参数进行建模的复杂性.

定义5在节点集合中，令某节点ch为标准服务器，其性能参数peh为1，则节点cj的性能参数pej为任务ωi在节点ch和cj上执行时间的比值，即pej=eth/etj=tih/tij.pej越大，则性能越好.

节点的负荷会影响动态性能.负荷越大，则其运行时间越长.衡量节点的负荷参数主要涉及任务到达数、任务离开数、瞬时队列长度、平均队列长度、平均响应时间、平均伸展系数、CPU利用率、未完成的工作量、可用资源情况、交付任务的要求等［3］.

考虑到本文算法是面向数据库系统的任务调度问题，可以将每个节点的当前数据库连接数作为单一负荷指标.过多的数据库连接会耗费大量的节点内存，占用大量的节点资源，导致节点处理速度变慢［4］.故采用数据库当前剩余的任务连接数liai(ai为节点ci上当前数据库连接数)和理论最大连接数li的比值以及节点的性能参数pei来表示节点当前的实时性能 ri，即 ri=pei(li-ai)/li.ri越大，则该节点当前的实时性能越好.

“着力解决问题最突出、矛盾最集中、群众要求最紧迫的水利问题，增强民生水利保障能力，扩大民生水利成果，使水利更好地惠泽民生，造福人民群众。”水利部部长陈雷的话语掷地有声，在代表们心中产生强烈共鸣。

2.6 非正常状态的判断和处理

为确保本文算法在执行时能从非正常状态中恢复，或不进入非正常状态，MPES算法设置了状态判断与处理.若节点集合C为空集，则当前系统没有资源，处于无可用资源状态，即等待状态.若在设定的调度窗口中，仅有一部分任务进入调度窗口，而这部分任务正好暂时没有可分配的资源，系统将长时间等待节点资源，此时系统处于假死状态.解决方法是重新设定调度窗口，允许更多的任务进入调度队列.可通过任务属性元素的循环跳数hi是否达到阈值来判断当前系统是否为假死状态，每当调度系统对任务ωi调度未成功一次，则hi加1.

当调度队列中所有任务的循环跳数均大于某一数值b时，则认为调度队列中所有任务在经过b次调度后均未成功，可以判断系统进入了假死状况.本文中设定b=5.

确定系统进入假死状况后，需要重新设定调度窗口.将调度队列集合Q中的任务再次进行预处理，根据优先级进行排队分别为q'1，q'2，q'3，其任务数分别为x，y，z.这3个队列的期望执行时间的最大值Temax可表示为

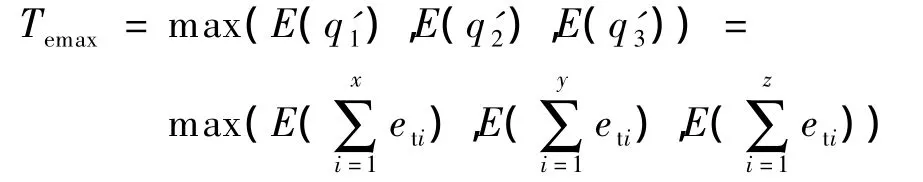
将q'1，q'2，q'3加入到等待调度队列的队首，即q1=q'1+q1，q2=q'2+q2，q3=q'3+q3，Qw=Q+Qw.重新根据MLLF策略进行排序，并对任务调度窗口重新设定.

如果期望执行时间的最大值Temax为普通优先级队列q'3的期望执行时间，即Temax=E(q'3)，则重新设定的调度窗口的标准时间值T=2Temax.根据2.2节所述，总调度窗口大小约为6T≈12Temax.

如果期望执行时间的最大值Temax为中等优先级队列q'2的期望执行时间，即Temax=E(q'2)，则重新设定的调度窗口的标准时间值T=Temax，总调度窗口大小为6T≈6Temax.

如果期望执行时间的最大值Temax为高优先级队列q'1的期望执行时间，即Temax=E(q'1)，则重新设定的调度窗口的标准时间值T=2Temax/3，总调度窗口大小为6T≈4Temax.

3 仿真试验

3.1 试验设计

试验在 GridSim工具包［5-7］下使用 Java语言实现，开发工具为NetBeans IDE 6.8.试验数据采用标准性能评估公司提供的2006年MetaCentrum集群的低负荷数据包和高负荷数据包.前者是MetaCentrum集群环境下17 d内476个节点资源和6×103个任务资源的集合，模拟了系统到达时任务数始终未超系统负荷的情况;后者是Meta-Centrum集群环境下50 d内1 152个节点资源和1.2×104个任务资源的集合，模拟了大量任务到达系统时系统始终处于超负荷运行的特殊情况.初始化GridSim的模拟环境和创建各种能力数据库资源后，得到的试验配置见表1和表2.按照本文算法开始调度，算法实现代码略.

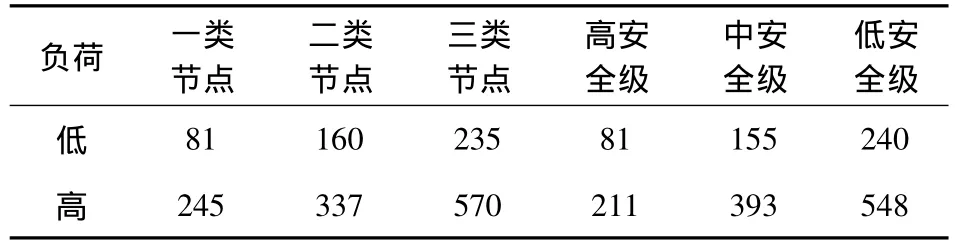
表1 各类属性节点数

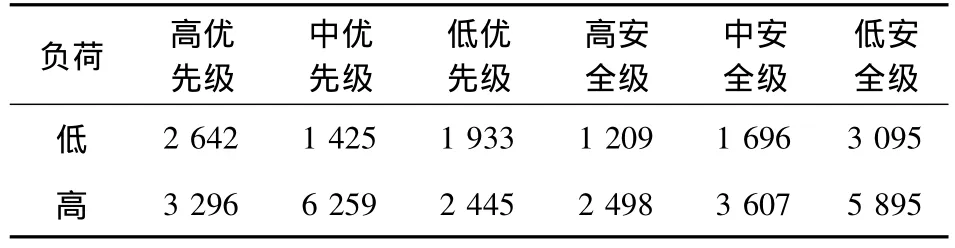
表2 各类属性任务数

3.2 结果分析

选择总服务时间Ts和公平度作为比较指标.总服务时间为所有任务的请求等待时间Tw与实际服务时间 Tss之和.不同负荷情况下，MCT算法［8］、Min-Min 算法［9］和 MPES 算法的等待时间、执行时间和服务时间比较见表3和表4.

表3 低负荷情况下服务时间比较 s

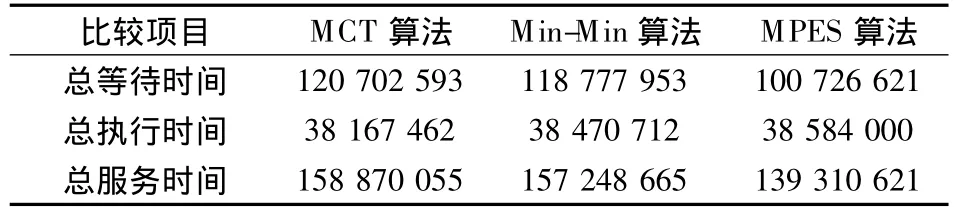
表4 高负荷情况下服务时间比较 s

3.2.1 服务时间的比较

要想提高任务计算效率，需要降低总服务时间，包括请求等待时间和实际服务时间(即执行时间).表3展示了低负荷数据包情况下3种时间的比较.由表可知，MPES算法的等待时间最短，这是因为MPES算法对任务进行排序，减少了运行时等待时间，且所得效果优于Min-Min算法.MCT算法和Min-Min算法都是选择将任务调度给执行最快的节点，而MPES算法则综合考虑节点性能和负荷，因此 MPES算法的执行时间较长.此外，MPES算法的总服务时间最长，较Min-Min算法多130 s，较MCT算法多96 s.MPES算法没有将任务调度给执行最快的节点，因此其执行时间较长;但与总服务时间相比，这是可以忽略不计的.

表4展示了高负荷数据包情况下3种时间的比较.由表可知，高负荷情况下的等待时间均远大于低负荷情况，且MPES算法的等待时间仍最短，因为其考虑了公平性和负荷均衡，减少了整体等待时间.MPES算法的总服务时间最少，分别比MCT算法和Min-Min算法减少了12.3%和11.4%，这是在减少了大量等待时间的情况下获得的.

3.2.2 调度成功率和公平度比较

高负荷下，MCT算法、Min-Min算法和MPES算法的调度成功率分别为94.03%，95.18%和96.23%;低负荷下则分别为 99.75%，99.75% 和99.80%.可见，MPES算法调度成功率是最高的，这是因为该算法是在综合考虑任务所需资源的满意度的基础上选择节点的.

队列之间的公平度可表示为［10］

f值越接近0，表明各队列之间的资源分配差异越小，公平性越好;反之，则表明各队列之间的资源分配差异越大，公平性越差.将表3和表4中的执行时间代入式(1)，可计算出MCT算法、Min-Min算法和MPES算法的公平度.在高负荷下，这3种算法的公平度分别为 0.051 90，0.051 89 和0.043 23;在低负荷下，3种算法的公平度基本相同，约为 0.008 14.

4 结语

调度算法的好坏直接影响着一个任务的运行时间和所耗资源.一个好的任务调度算法应该能够充分合理地利用网络环境中各种可用资源，并让这些资源以最高效的方式协同工作.MPES算法以气象水文分布式数据库应用环境为研究背景，综合优先级、公平性、资源映射代价、安全性和负荷均衡等策略要素，在任务调度成功率、服务效率和公平性上较已有的MCT算法和Min-Min算法有显著提高，特别是在高负荷情况下其总服务时间明显减少.

References)

［1］朱海，王宇平.多目标约束的网格任务安全调度模型及算法研究［J］.电子与信息学报，2010，32(4):988-992.Zhu Hai，Wang Yuping.Constrained multi-objective grid task security scheduling model and algorithm［J］.Journal of Electronics ＆ Information Technology，2010，32(4):988-992.(in Chinese)

［2］Laplante P A.Real-time system design and analysis［M］.3rd ed.London:Prentice Hall，2004:147-156.

［3］Henderson J，Lemon O，Georgila K.Hybrid reinforcement/supervised learning of dialogue policies from fixed data sets［J］.Computational Linguistics，2008，34(4):487-511.

［4］杨忠明，秦勇，黄翰，等.复杂网格的演化及其在Internet负荷平衡中的应用研究［J］.计算机工程与科学，2011，33(2):37-41.Yang Zhongming，Qin Yong，Huang Han，et al.Research on the evolution of complex and their application in Internet balancing［J］.Computer Engineering ＆ Science，2011，33(2):37-41.(in Chinese)

［5］Sulistio A，Poduval G，Buyya R，et al.On incorporating differentiated levels of networks service into Grid-Sim［J］.Future Generation Computer Systems，2007，23(4):606-615.

［6］Sulistio A，Cibej U，Venugopal S，et al.A toolkit for modelling and simulating data grids:an extension to GridSim［J］.Concurrency and Computation:Practice and Experience，2008，20(13):1591-1096.

［7］Qureshi K，Rehman A，Manuel P.Enhanced GridSim architecture with load balancing［J］.The Journal of Supercomputing，2011，57(3):265-275.

［8］Fidanova S.Simulated annealing for grid scheduling problem［C］//Proceedings of IEEE John Vincent Atanasoff 2006 International Symposium on Modern Computing.Sofia，Bulgaria，2006:41-45.

［9］Chauhan S S，Joshi R C.A weighted mean time Min-Min Max-Min selective scheduling strategy for independent tasks on grid［C］//Proceedings of the 2nd IEEE International Advance Computing Conference.Patiala，India，2010:4-9.

［10］彭娜，王运送，聂思举，等.我国民族地区城乡收入差异程度的实证分析［J］.中央民族大学学报:自然科学版，2011，20(4):74-77.Peng Na，Wang Yunsong，Nie Siju，et al.The empirical analysis of urban-rural income gaps in ethnic areas of China［J］.Journal of Central University for Nationalities:Natural Sciences Edition，2011，20(4):74-77.(in Chinese)