OLAP聚集计算中的维存储技术

宋爱波 张若儒 赵经华 何战国

(东南大学计算机科学与工程学院，南京211189)

OLAP是一种针对数据仓库中的数据进行联 机访问和分析的主要技术［1］.然而，传统DBMS的行存储结构严重制约了OLAP聚集计算效率.按行存储和读取数据适合以写操作为主的事务处理，不适于以读操作为主的OLAP.早期的列存储模型DSM 是由 Copeland等［2］在1985年提出的.DSM将每个关系按列进行垂直划分，将每个列值以(元组ID，列值)对形式进行存储.在列存储中，只有被查询的列才会读入内存，而行存储需要读入所有列，因此列存储比行存储具有更高的数据查询效率.此外，列存储还具有更高的数据压缩比.如今，商业 列 数 据 库 有 SenSage［3］，Sybase IQ［4］，Big-Table［5］等，开 源 列 数 据 库 有 MonetDB［6］，C-store［7］，HBase［8］等.根据 Feinberg 等［9］在 2011年1月关于数据仓库的分析报告，与传统关系型数据库相比，列数据库在数据分析(包括OLAP等)方面表现出卓越的性能.

目前，Sybase IQ还不能很好地支持高维OLAP数据的维层次特性，可扩展性较差.Zou等［10］建立在HBase上的索引表CCindex能较好地支持范围查询，但没有考虑数据的层次性.文献［11］提出的维层次编码能够支持OLAP的多维层次性，但是其B+树的传统构建方法产生的开销太大，且仍采用行存储结构，读取大规模列数据时效率不高.

HBase是BigTable的开源实现，以HDFS(Hadoop分布式文件系统)为底层存储，是一个提供高可靠性、高性能、列存储、实时读写的大规模分布式数据库系统.在HBase中，列可动态扩展，能较好地支持OLAP数据的维层次属性;它还能利用Hadoop系统的MapReduce框架对列数据进行高效并行计算.鉴于此，本文提出了一种基于 HBase的OLAP维存储模型，采用自底向上的方法构建维层次编码B+树索引，避免了利用传统的自顶向下方法进行分裂操作所造成的巨大开销，因而可以快速获取任意维层次的OLAP数据，更好地支持上层OLAP的聚集运算.

1 维存储

本节介绍了OLAP多维数据模型和HBase存储机制，给出OLAP维存储模型在HBase上的实现，为生成基于维层次编码的B+树索引提供支持.

1.1 OLAP多维数据模型

OLAP多维数据在数据仓库中一般以星型模式组织，即将若干个维表以事实表为中心联系起来(见图1)［12］.为构建这一星型模型，首先要确定度量属性，也就是人们对其值感兴趣的属性，余下的属性则作为维属性.图1中，将销售数量(SaleNum)和总量(Quantity)这2个属性作为度量属性.维用于表示人们观察度量值的特定角度;比如地区维，即可以根据地区来统计某个产品的数量.

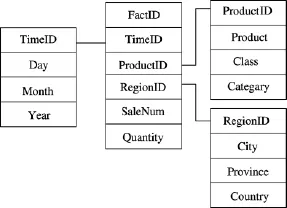
图1 星型模式

维通常具有层次性.若维中属性之间可以进行度量比较，则将这种属性称作维的层次.如时间维中有年、月、日3个层次，日的信息可以通过上卷操作转换为月或年的信息，年的信息可以通过下钻操作转换为月或日的信息.

1.2 HBase存储机制

HBase在概念上以表的形式存储数据(见表1)，但在物理上则按照列族进行存储(见表2和表3).表由行和列组成，所有列被划分为若干个列族.通过行和列确定的一个存贮单元称为Cell.每个Cell都可以保存多个版本的数据，通过时间戳来索引.行关键字是用来检索记录的主键，通过主键或主键加时间戳可以定位一行数据.

一张表先被横向划分成多块，每块称为一个Region，数据按照行主键的字典序排序存储;在Region中数据再按列族划分，存储在HDFS上.

表1 HBase数据存储的概念视图

表2 列族A存储的物理视图

表3 列族B存储的物理视图

1.3 基于HBase的OLAP维存储模型

OLAP维存储模型以(维层次编码，度量值)对形式重新组织OLAP多维数据，用于支持基于维层次编码的B+树索引，使其根据维层次编码一次性查找到相应度量值，避免每次查询都要进行维表与事实表的连接操作.维值经过编码后，其占用的存储空间大大减少.

在HBase中，首先根据星型模式分别存储事实表和维表.存储维表时，每个维的所有属性形成一个列族，每个属性是一个列.将事实表中的维属性集和度量属性集定义为不同列族.以图1中的多维数据模型为例，其在HBase中的事实表见表4，时间维表见表5，其他维表类似于时间维.

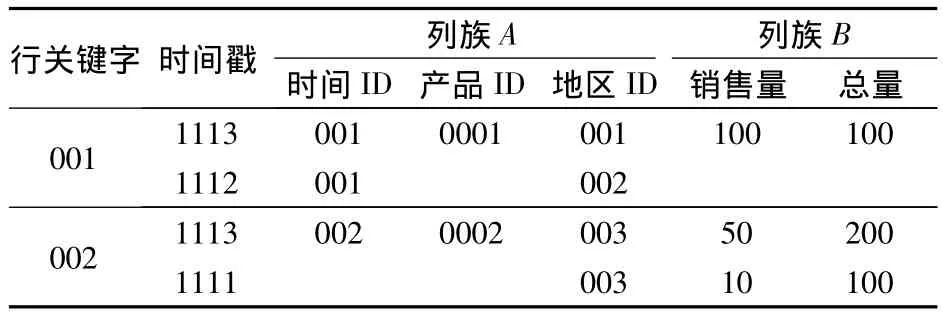
表4 HBase中事实表存储的概念视图

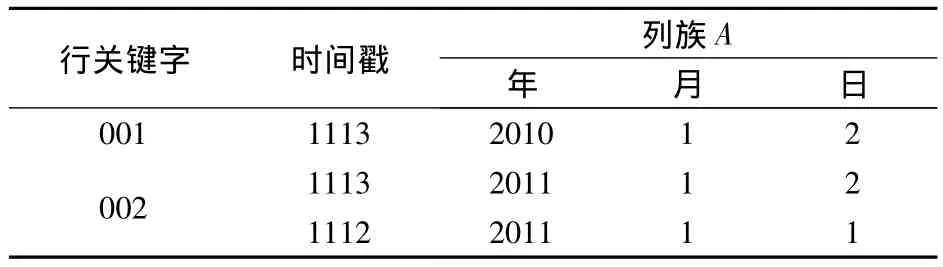
表5 HBase中时间维表存储的概念视图

定义好各表的模式后，对OLAP多维数据中具有层次性的维进行维层次编码.

定义1维层次树可以形式化定义为DTree=(V，E).其中，V为维中各个层次的所有成员的有序集;E为各个成员之间的层次关系，即维层次树中的边连接关系.如时间维从上往下的层次为(年，月，日)，其维层次树如图2所示.

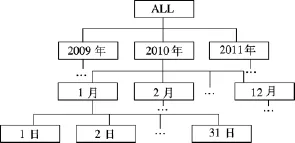
图2 时间维的维层次树

定义2Pij(j∈1，2，…，v)为维表 Di中的第 j层属性集(j值越大，其在层次树中的层次越低)，其值域为

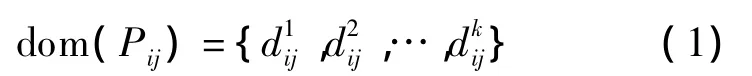
式中，dij为维表Di中的第j层属性;k为第j层不同属性的个数.

定义3dom(Pij)中各成员的二进制编码为BPij，其值域为

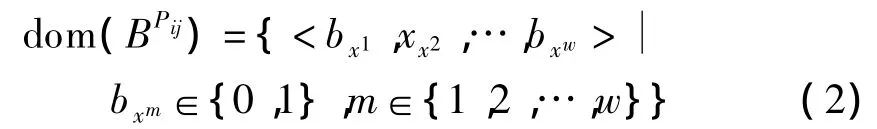
式中，w为Pij中各属性成员的二进制编码位数，其最小取值为α(log2k)，α为向上取整运算.如图2所示，在时间维中，年层次有3个不同属性值，则年层次中k=3，月层次和日层次中k分别为12和31.为了应用的扩展，为某些成员不确定的层次(如年层次)预留一些编码位数，即取 w＞α(log2k);而对于成员中确定的层次(如月层次上只有12个月)，则w=α(log212)=4.对一个维的每个层次生成一个二进制编码表.时间维的维层次属性二进制编码表见表6.

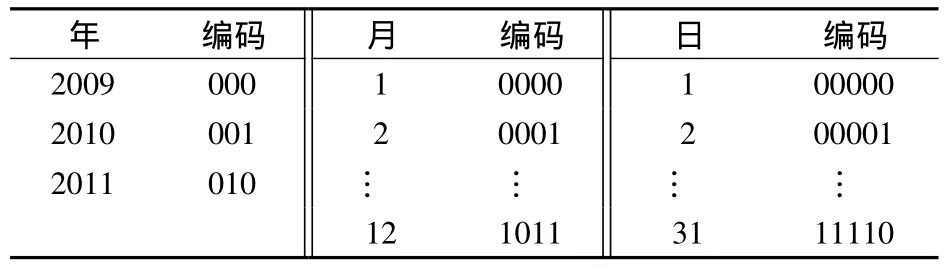
表6 时间维的维层次属性二进制编码表

定义4维表Di中，主键为Ks(长度为LKs)、时间戳为Tt(长度为LTt)的维值的维层次编码可表示为

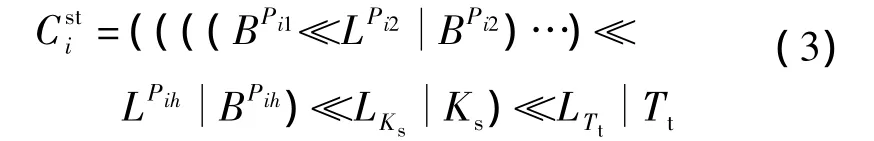
该维层次编码是由各层次的二进制编码按层次由高到低组合起来，再加上每个事实表记录的主键和时间戳所构成的.主键和时间戳组合的唯一性，确保了维层次编码的唯一性.

传统的OLAP聚集计算难以避免维表与事实表间的多次连接操作，是造成其效率低下的原因之一.为解决该问题，对于每个维表，通过一次与事实表的连接操作，预先将维值与度量值关联起来，以(维层次编码，度量值)对的形式保存在HBase中，由此便可通过层次编码的B+树索引直接查询到度量值，大大提高了查询效率.以表5为例，根据表6进行编码，同时将表4和表5在时间ID上进行连接，获取事实表记录的主键和度量值，便可以得到该维的维层次编码-度量表(见表7).

表7 时间维的维层次编码-度量表

维存储模型利用了HBase能动态地在列族中增删和更新列的特性，有利于对多维数据模型的扩展.要增加或删除一个维，只需在HBase中增加或删除一个维表即可;对某个维中的属性进行增删或更新时，仅需对HBase中相应维表的对应列进行操作.这种维存储模型可以方便地动态更新维和维中属性，因而能够适应多种应用及扩展.

2 基于维层次编码的B+树索引

索引管理是数据访问管理的重要内容.索引是对数据库表中一个或多个列的值进行排序的结构.在经常查询的数据上建立索引，是提高查询效率最为简单有效的方法.B+树是在数据库中索引普遍应用的数据结构，具有高效、灵活等优点.

2.1 B+树的定义

B+树索引是一颗分层的平衡树，树中的节点分为2种类型:叶子节点和中间节点.

定义5一棵m阶B+树或者为空，或者满足下列性质:

1)中间节点最多有n棵子树，且结构为s，A0，(Z1，A1)，(Z2，A2)，…，(Zs，As).其中，Al为子树指针，0≤l≤s≤n;Zl为关键字，且 Zl＜ Zl+1.所有中间节点的关键字互不相同.

2)子树Al中的所有关键字都大于等于Zl并小于Zl+1.子树As中的所有关键字都大于等于Zs，子树A0中的所有关键字都小于Z1.

3)根节点至少有2棵子树，其他中间节点至少有α(n/2)棵子树.

4)所有叶子节点都处于同一个层次，包含了全部关键字以及相应的数据或数据地址.当其包含数据时，称之为聚簇索引;当其包含数据地址时，称之为非聚簇索引.

在聚簇索引中，数据的索引顺序与物理顺序相同;在非聚簇索引中，数据的索引顺序与物理顺序没有必然联系.通常，聚簇索引有利于范围查询，而非聚簇索引有利于单行查询.

深秋的山野飘溢着浓郁的花香，这东泉岭上像是一个天然的分界线，上面似乎永远的云雾缭绕，站在这里总会有云朵飘逸过来，下面则草木郁郁葱葱，直抵山下的村子，充满着人间的烟火味。风影的脸上带有几分落寞，这大千世界在他眼里成了一座迷宫，不管怎么走都走不到尽头，找不到出口。这个世界要说简单其实非常的简单，可要是复杂起来，那简直就是一个蛛网密布永远纠结不清的阴阳八卦图。风影感到了从未有过的迷茫，这红尘世界离他越来越远，他的神经末梢只能感觉到一点点轻微的颤动。

2.2 B+树索引的创建

考虑在OLAP维存储中，通常只是按照维值查找数据，而且聚集计算通常要进行大规模的范围查询，因此本文采用B+树的聚簇索引.在B+树的生成上，采用自底向上构建的方法，避免了传统的自顶向下插入法所造成的巨大节点分裂开销.

在建立B+树时，关键字是维层次编码，数据是度量值.自底向上构造B+树需要满足以下2个条件:①查找键值已排序;②查找键不含重复值.在构建的维层次编码-度量表中，维层次编码的有序性和唯一性满足这2个条件.

叶子节点所在层次被称为第0层，叶子节点以上层数依次递增.B+树的建立是一个自底向上反复迭代的过程，共有3层循环.内层循环用于向新申请的节点块中填充关键字;第2层循环用于申请一个新的节点;最外层循环对每一层节点进行管理.若在第2层循环结束后，只创建了一个节点块，则说明该节点是根节点，保存根节点信息后，最外层循环结束，B+树创建完毕.

2.3 B+树索引的查找

基于维层次编码的B+树索引的查找主要包括以下3个步骤:

①根据要查找的维值和提供的主键(可选)、时间戳(可选)，生成该维值的维层次编码C，将C作为查找的关键字.若不提供主键或时间戳，则将C中对应主键或时间戳的编码置为0，此时的查找结果可能会有多个.如果查询请求同时提供了维值、主键和时间戳，则查找结果最多只有1个.

②执行B+树的查找算法.首先判断查找关键字的值是否小于根节点的第1个关键字，条件成立则说明它比所有值都小，查找失败;然后从根节点开始，找到符合条件的关键字，根据其指针找到下一层的节点，直到在叶子节点中找到符合条件的第1个数据项.若没有符合条件的结果，则查找失败;若查找成功，则返回数据块号和第1个数据项的槽号.

③若第2步中查找成功，且查找的关键字中主键和(或)时间戳的编码为0，则从第2步中获得的块首地址和槽号开始进行扫描，查找所有除去主键和(或)时间戳部分编码后与关键字相同的数据项，将其作为查询结果返回，并记录数据项的个数.

2.4 B+树索引的更新

当向数据库中追加数据时，也会向B+树中追加索引.当B+树中的节点块满时，会发生分裂.与传统方法构建的B+树不同，此时的分裂操作仅涉及到每一层的最后一个节点，且不是将原有节点分裂，而是在申请到一个新节点块后，直接把新索引项追加到新节点中.当根节点分裂时，会申请2个新节点块，其中一个作为新的根块，原来的根节点成为普通的节点.

一个节点块能索引多个数据项;当追加数据时，索引块分裂的几率很小.因此，B+树的更新比传统方法构建的B+树简单许多，体现在以下几个方面:

1)向数据块中追加数据时，索引信息不一定会发生修改.

2)需要修改索引信息时，只需要提供待追加的维层次编码和新建数据块的块号.

3)可以在操作前从根节点开始，依次读出每一层中最后一个节点块的块号，将其保存在缓冲区中.待需要向上分裂时，可以重复调用此块号.

3 性能分析

3.1 列存储和行存储

在数据仓库环境中，通常是周期性地装载大量新数据，在此后较长的一段时间内进行大量的实时查询，且查询主要是对大量列数据的聚合操作.

首先，列存储能提高查询所需列数据的吞吐量，减少I/O操作.查询语句中的谓词是基于列来定义的，列存储可以快速锁定该列数据，不会检索无关列的数据，避免了行存储中大量无效的磁盘I/O操作.尤其是在表的列数较多时，性能的提升会更加明显.例如，一个表有5×107条记录，每条记录占用1 KB，平均每列数据占用10 B.在行存储模式下，对某列数据进行聚集操作，假设磁盘块大小为64 KB，则需进行5×107×1 KB/64 KB=781 250次I/O操作.在列存储模式下，只需读取该列数据，进行5×107×10 B/64 KB=7 630次I/O操作.由此可见，列存储的查询效率比行存储提高了上百倍.

此外，列存储在数据压缩方面也比行存储具有优势.同一列的数据具有相同的数据类型，数据的相似度比较大.行存储中不同列有不同的数据类型，很难为多种数据类型选择一个合适的压缩算法.将压缩算法应用于列存储数据库中，可以降低数据的存储空间，进而降低磁盘同步和数据导入时间.

HBase和MySQL导入数据的时间比较见表8.由表可知，列数据库 HBase相比行数据库MySQL在导入数据时间上具有明显优势.

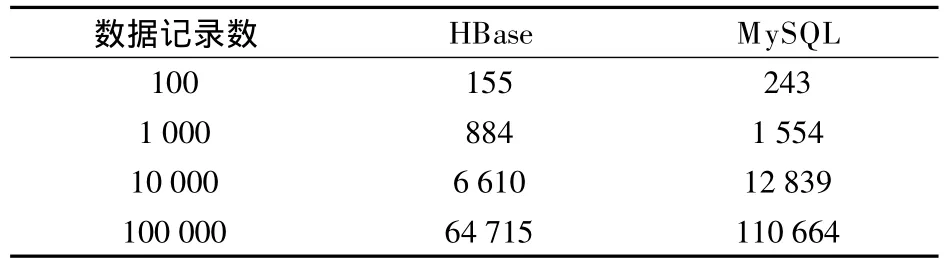
表8 HBase和MySQL导入数据时间比较 ms

3.2 B+树索引

B+树上操作的时间通常由存取磁盘的时间和CPU计算时间构成.与高速的CPU计算相比，磁盘I/O操作慢很多，因此可忽略CPU的计算时间，只分析磁盘访问次数.

设一个维上B+树索引的节点数为M，高度为h，最小度数t≥2，由B+树的性质可知

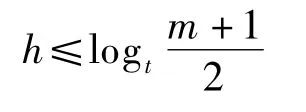
索引的创建采用自底向上的方法，无需分裂操作，存入磁盘的时间复杂度为O(M).一次查询需要读磁盘O(h)=O(logtM)次，对关键字进行扫描的次数不超过2t，故查询操作总的时间复杂度为O(th)=O(tlogtM).索引的更新可能需要申请新的节点.在最坏情况下，每层最后一个节点均已包含最大关键字数，添加新的索引项需要递归向上层申请新节点，访问磁盘的时间复杂度为O(h)=O(logtM).

将维层次编码代替原关键字，可大大降低存储空间.若维成员个数共计256个，简单位图索引中的编码需要256 bit，而维层次编码只需8 bit，数据压缩比为32.随着维成员个数的增加，数据压缩比呈指数型增长.同时，维层次编码的压缩效果约是整数编码的3～4倍.

3.3 可扩展性分析

HBase中，可在列族中动态增删某个列.利用这一特点，可以根据应用场景动态增加或删除某个维和某个度量.在基本事实表中，定义维族和度量族2个列族，维族中将每个维定义为一个列，度量族中将每个度量定义为一个列.增删某个维后需将对应的B+树索引进行增删;增删某个度量后，需在每个维的维层次编码-度量表的度量列族中增删对应的度量列.可见，在维和度量属性上，本文算法具有较好的可扩展性.

4 结语

本文分析了当前OLAP聚集计算的现状，在研究 OLAP数据模型和列存储的基础上，根据OLAP从维角度查询度量值的特性，提出了一种OLAP维存储模型，利用HBase的列存储机制高效地管理了OLAP多维数据.在此基础上，提出了一种自底向上构建基于维层次编码的B+树索引的方法，提高了对OLAP海量多维数据查询的效率，为上层OLAP聚集计算提供了有效的支持.

References)

［1］Chaudhuri S，Dayal U.An overview of data warehousing and OLAP technology ［J］.SIGMOD Record，1997，26(1):65-74.

［2］Copeland G P，Khoshafian S N.A decomposition storage model［C］//Proceedings of the 1985 ACM SIGMOD International Conference on Management of Data.New York，USA，1985:268-279.

［3］Neil Roiter.SenSage opens SIEM data to business intelligence tools［EB/OL］.(2011-02-04)［2011-05-05］.http://www. networkcomputing. com/wan-security/sensage-opens-siem-data-to-business-intelligence-tools.php.

［4］罗润升.Sybase IQ红宝书［M］.北京:中国水利水电出版社，2008:2-5.

［5］Chang F，Dean J，Ghemawat S，et al.BigTable:a distributed storage system for structured data［J］.ACM Transactions on Computer Systems，2006，26(2):4-8.

［6］Vermeij M，Quak W，Kersten M，et al.MonetDB，a novel spatial column-store DBMS［EB/OL］.(2008-10-31)［2011-05-05］.http://www.gdmc.nl/publications/2008/MonetDB.pdf.

［7］Stonebraker M，Abadi D J，Batkin A，et al.C-store:a column-oriented DBMS［C］//Proceedings of the 31st International Conference on Very Large Data Bases.Trondheim，Norway，2005:553-564.

［8］Hadoop Wiki.HBase:bigtable-like structured storage for Hadoop HDFS［EB/OL］.(2012-02-23)［2012-04-17］.http://wiki.apache.org/hadoop/Hbase.

［9］Feinberg D，Beyer M A.Magic quadrant for data warehouse database management systems［EB/OL］.(2011-01-28)［2011-05-05］.http://www.sybase.com/files/White_Papers/Gartner_MagicQuad_forDataWarehouse-DMS.pdf.

［10］Zou Yongqiang，Liu Jia，Wang Shicai.CCIndex:a complemental clustering index on distributed ordered tables for multi-dimensional range queries［J］.Lecture Notes in Computer Science，2010，6289:247-261.

［11］张延鹏.Data Cube中基于维层次的OLAP算法研究［D］.秦皇岛:燕山大学信息科学与工程学院，2010.

［12］Karayaxmidis N，Tsois A，Sellis T，et al.Processing star querieson hierarchically-clustered facttables［C］//Proceedings of the 28th International Conference on Very Large Data Bases.Hong Kong，China，2002:730-741.