基于密度可达的聚类隐私保护模型

贺玉芝 倪巍伟 张 勇

(东南大学计算机科学与工程学院，南京210096)

在数据隐私安全保护备受关注的今天，面向挖掘任务的隐私保护微数据［1］(个体数据，区别于统计数据)发布已成为研究的一个热点.它在“保护数据隐私”与“挖掘知识”间寻求折中，要求发布后的数据不泄露原始微数据隐私信息的同时，还具有较好的挖掘可用性.隐私保护微数据发布通常采用改变微数据取值的思想实现对数据隐私的保护，聚类通过对数据个体间相似/异性的分析对数据进行聚簇.隐私保护微数据发布弱化了个体数据差异和聚类依赖个体数据差异的矛盾，使得面向聚类的隐私保护微数据发布成为一个难点.

数据隐藏发布中，隐私模型用于对所需保护的隐私模式和数据可用性加以定义，使得隐藏方法具有可比性和通用性.在基于限制发布技术的研究方面，Sweeney［1］提出的 k-匿名原则，要求所发布数据表中的每一条记录的非敏感属性不能区分于其他k-1条记录，并称不能相互区分的k条记录为一个等价类.k-匿名只针对非敏感属性进行约束，使攻击者可以通过一致性攻击和背景知识攻击，识别敏感数据与个人的对应关系.针对这一问题，文献［2］提出了保证等价类敏感属性至少有l个不同值的l-diversity模型.针对数值型敏感属性数据发布，范围攻击是最大潜在攻击.为了对其提供更好的保护，(k，e)-匿名模型［3］在 k-匿名基础上，要求最大和最小的敏感属性差值至少为e.这种界定忽略了总体数据分布，对于数值集中分布在最大或最小一端的情况，仍造成了隐私信息的泄露.文献［4］的(ε，m)-模型对(k，e)-模型进行了改进，要求等价类中最多1/m的记录的属性值相似，相似程度由ε决定.面向数据挖掘应用的隐私模型方面，文献［5］提出适用于交易型数据频繁项集挖掘的隐私模型，定义了public属性和private属性上的moles(非频繁项集)和nuggets(频繁项集)，并提出消除moles的同时最大限度保留nuggets的方法.

聚类过程直接依赖于数据点间的微观距离，但聚类结果可由宏观上相近的数据邻域分布情况来间接保证.因此，在面向聚类的隐私保护数据发布研究方面，大多数数据隐藏方法采用从微观上保距或从宏观上保分布，以保证数据隐藏后的聚类可用性.其中，Oliveira等［6-7］提出基于几何数据转换的干扰方法RBT，通过保证隐藏后数据记录间距离不变实现聚类可用性，该方法在泄露任意2条扰动前后的数据记录情形下，攻击者就能逆推所有原始数据，存在数据隐私安全性低的不足.文献［8］提出了基于对象相似(OSBR)和维度约简(DRBT)的干扰算法，利用将高维数据随机投影到低维空间的方法，对原始数据进行干扰，以实现隐私数据的保护和聚类可用性的维持.文献［9］提出一种面向聚类的启发式匿名数据发布方法，对干扰前后的数据进行聚类模式比较，确保聚类差异满足设置的阈值，实现干扰处理的合理性.文献［10］提出一种基于邻域属性熵的数据干扰方法，通过维持原始数据的k邻域关系的稳定，来保证数据干扰发布后有较好的聚类可用性，但数据扰动幅度具有一定的局限性，易导致范围攻击.文献［11］单独考虑数据的每个维度，对单一维度内的数值进行近邻交换，以破坏数据固有的内在对应关系，从而实现数据隐私保护，该方法不仅存在隐私安全性低、聚类可用性差的不足，还对近邻参数c有较大的限制(c达到一定程度，树的搜索空间过大).文献［12］通过建立最小生成树，将一条边的邻近点的非敏感属性用它们的均值替换，以保护敏感属性，同时也保持干扰后数据集的均值和方差不变，若将b条邻近记录的准标识符用均值来替换，b个记录中的敏感属性值的种类数为n，则敏感属性泄露的概率为n/b，存在隐私泄露隐患.

上述2种策略存在如下问题:扰动方法［6-8］不具备通用性，不同数据分布的数据集安全性和聚类可用性偏差较大;已有的隐私模型［1-5］难以直接应用到面向聚类建模的问题中.本文将建立一个具有通用性的隐私模型，同时设计一个基于模型的数据隐藏方法.

1 问题描述

在隐私保护数据发布领域中，数据隐私模型旨在定义隐私规则约束，形成所需保护的隐私模式.设原始数据集(多维数值型)为D，本文将定义相应隐私规则约束，建立隐私保护模型，并设计一个基于模型约束的数据隐藏算法，对数据集D实施干扰，干扰后的数据集为D'，要求保证D'在满足隐私模型约束的同时，具有与D相同或相似的聚类结果.

本文针对多维数值型数据集，从数据邻域角度出发，通过对邻域内点的数目以及数据点分布的限制，来构建面向聚类的隐私保护模型.下面给出几个定义.

定义1(近邻域)设数据点p，o∈D，落入以p为中心、ε为半径圆域的所有数据点称为p的近邻域点 Nε(p)，即，且p近邻点数目为CNε(p).

定义2(核心点)设数据点p∈D，当p在ε内的近邻点数目不小于r时称 p为核心点，即，其中 r为与 ε邻域相关的阈值参数.

定义3(密度可达邻域)设数据点p∈D，o∈Nε(p)，p在ε内的密度可达近邻域为NBDε(p)={Nε(p)∪NBDε(o)，o∈kernelε}，密度可达邻域内点的数目为CNBDε(p).

如图1所示，点p，o，q的近邻域分别为以该点为中心的圆域.设r=10，由于p及其近邻域内的点o和q均为核心点(其近邻域点的数目不小于10)，因此，p的密度可达邻域包含3个圆域中所有的点.

定义4(近邻攻击)设数据点p∈D，当p的ε内近邻数目CNε(p)＜r时，邻域较稀疏，数据点易被揭露，由此带来的攻击称为近邻攻击，为防范近邻攻击发生，要求CNε(p)≥r.

图1 近邻域和密度可达邻域

定义4仅对近邻点的数目和距离添加约束，忽略了数据分布，不足以防范范围攻击，如图2所示，设r=10，图中数据点的数目完全满足不小于10的约束，但数据点仍集中分布在较小范围内.此外，虽然对于凸状球形数据集而言，这种约束是良性的，但对非均匀球状分布的数据集而言，这种约束将使各聚簇界限趋于模糊，导致数据集的聚类结果极不理想.例如，对于图3中的数据分布情况，要使每个数据点近邻域内点的数目达到所设定的约束，可能导致聚簇界限模糊.

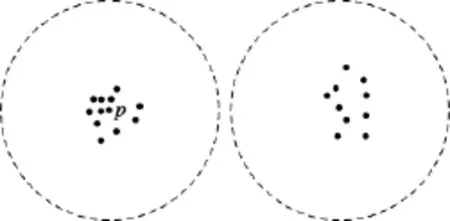
图2 集中分布

图3 非球形的不规则分布

定义5(密度可达近邻攻击)设数据点p∈D，h为自定义参数(h＞r)，当p的ε密度可达邻域内近邻数目CNBDε(p)＜h，则它将遭受密度可达近邻攻击，为防范此类攻击，要求CNBDε(p)≥h.

定义6(密度可达安全邻域)设数据点p∈D，当 CNBDε(p)≥h时，称 p为安全点，且当NBDε(p)邻域内部的点都为安全点时，称p密度可达邻域为安全邻域.

性质1(核心点的安全传递性)设数据点p∈D，若p为核心点，且 p是安全点，则NBDε(p)邻域内部的点都为安全点，即p密度可达邻域为安全邻域.

证明依据密度可达邻域的递归定义，可知密度可达邻域是通过核心点扩张的邻域集.因此，核心点具备传递性，若从核心点p出发，到达最远的点为q，则q必然也能逆向到达p，因此NBDε(p)=NBDε(q)，CNBDε(p)=CNBDε(q)≥h.证毕.

近邻攻击只对近邻数目和距离进行约束，容易忽略由数据集的总体分布带来的范围攻击，而基于密度的可达近邻攻击，旨在利用核心点的可扩展性和安全传递性，间接地调整数据点的分布，让孤立群体向核心点靠近，用以防范孤立群体聚集造成的范围攻击.根据上述定义和性质，构建以下聚类隐私保护模型.

定义7(PPC(r，ε，h)隐私模型约束)设数据点p∈D，r，h为自定义参数(h＞r)，若隐藏后数据表中任意记录p满足其ε密度可达邻域内近邻数目不小于h(即CNBDε(p)≥h)，称隐藏后数据表满足PPC(r，ε，h)隐私模型约束，其中密度可达邻域基于核心点扩展，参数由r决定.

2 聚类隐私模型构建算法PPC(r，ε，h)

隐私模型构建算法的流程如下:对空间数据点集合D中数据点p，给定参数r，ε，h(h＞r)，得到p的ε邻域Nε(p)以及密度可达邻域NBDε(p).设T=kernelε，S=Nε(p)-T，即 T 为 p 的 ε 邻域内核心点的集合，S为p的ε邻域内非核心点的集合.参照核心点的安全传递性，算法总是从高密度区域的点 p开始排查，若 CNBDε(p)≥h，标记NBDε(p)内所有点为安全点;否则，从S中任选点q，对Nε(q)-Nε(p)差集中的数据点进行平移操作，使q成为核心点.依此使更多的非核心点成为核心点，扩张可达邻域，使p的ε可达邻域为安全域.当CNBDε(p)≥h，则转向其他不安全点;否则，继续选择p的非核心近邻执行平移操作，若最终无法生成满足约束的ε可达安全邻域，则不发布p以及邻域内可达数据点.

在此过程中，若初始T不为空，即存在核心点p，根据性质1使 p和 q的邻域合并，迅速扩张反之，若不存在核心点p，则从q出发扩张和平移，使q成为核心点.

2.1 平移技术

平移旨在将非核心点q变成核心点，因此，每次都用r-CNε(q)计算应该加入的数据点数目shiftnum，然后在Nε(p)-Nε(q)差集内(简记为p-q)找到距离q最近的shiftnum个数据点，并求其ε邻域的交集，任选交集内的点o作为q的目标点，将q以及Nε(q)-Nε(p)差集(简记为 q-p)中的数据点都按照平移向量进行平移.如图 4 所示，p是核心点(r=10)，但非安全点，q是p邻域内的非核心点，CNε(q)=7(图4中q及其邻域内另外6个点)，还需加入shiftnum=3个点q就能成为核心点.图5 中的点 o1，o2，o3为 Nε(p)-Nε(q)内距q最近的3个点，o为三者ε邻域交集中的点，按照平移向量对 q 以及 Nε(q)-Nε(p)差集的点进行平移即可.性质2和3详细地叙述了对多个数据点求ε邻域交集的方法.

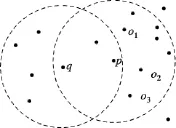
图4 非核心点q

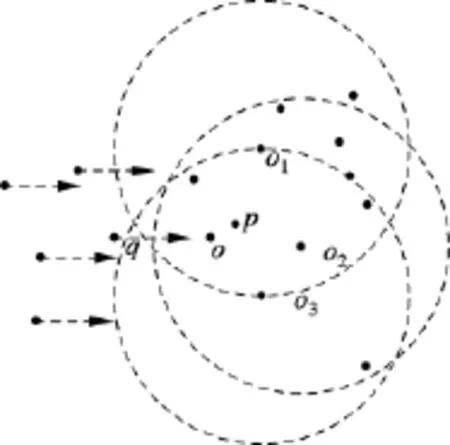
图5 q－p邻域内的点向o点平移

性质2对p点ε邻域内的多个点o1，o2，…，oi，…，om的ε圆域求交集，一定有解.

证明已知集合 A=Nε(p)，oi∈A(1≤i≤m)，即对于所有 oi有d(oi，p)≤ε，假设交集内不存在解，即不存在一个点o使点o的ε邻域内同时出现 o1，o2，…，oi，…，om，即对于所有 oi没有点 o使得d(oi，o)≤ε，然而根据已知对于所有 oi有d(oi，p)≤ε，即p是一个特殊的o，这与假设不符，因此，对 p 点邻域内的多个点 o1，o2，…，oi，…，om的ε邻域求交集，一定有解.

性质3对p点ε邻域内的多个点o1，o2，…，oi，…，om的ε圆域求交集(设为B)，假设o是 oi中距p最远的点，则以p为圆心、ε-d(o，p)为半径的圆域C∈B.

证明如图6所示，已知集合A=Nε(p)，oi∈A(1≤i≤m)，即对于所有 oi有 d(oi，p)≤ε，o是 oi中距 p 最远的点，即 d(oi，p)≤d(o，p)≤ε，小圆C的半径r=ε-d(o，p)，则根据圆的性质可知，圆外一点o到圆C的距离小于等于r+d(o，p)，即圆C内任意一点pi到o的距离d(o，pi)≤r+d(o，p)≤ε -d(o，p)+d(o，p)≤ε，同理，对于其他 oi点，d(oi，pi)≤r+d(oi，p)≤r+d(o，p)≤ε，即以p为圆心、ε-d(o，p)为半径的小圆内的任意一点到oi的距离都不大于ε.

图6 多点圆域的交集

求解多个点的圆域的交集时需要将繁杂的多个不等式联立，对于多维的数据点需要建立多元不等式，程序的求解更是一个无限穷举的过程.而利用上述性质，只需在以p为圆心、ε-d(o，p)为半径的小圆内任意选一个点即可，大大降低了时间复杂度.

2.2 平移优化

在2.1节设计的平移方法中，选择候选近邻点q的方法较为粗略，本节将对此进行改进.

1)快速扩张

在探查候选近邻点时，每探查一个候选点，便要计算一次平移长度和平移方向.为减少计算时间，引入近邻价值的概念:

定义8(近邻价值)设数据点 p∈D，q∈Nε(p)，定义

近邻价值以差集的大小衡量，每次选择非核心近邻q时，总是贪心地选择具有最高价值的q使其成为核心点，因为这样的q总能最快地扩张安全域的大小，从而尽量减少探查候选点的次数.

2)安全扩张

在探查候选近邻点时，若只从价值上贪心地选择具有最高价值的近邻平移，可能将邻域内远离其他点的点优先作为候选点，即将原本最不相似的点变成相似的点，不利于聚类可用性的保持.为此，选择候选点时还需考虑邻域相似性.

定义9(邻域相似性)设数据点p∈D，q∈Nε(p)，邻域内 p和 q的相似性 s(p，q)=邻域内邻域相似性均值

因此，在贪心选择具有最高价值近邻的同时，规定p邻域内的非核心近邻满足邻域相似性大于s(p)的近邻q为候选近邻.

PPC(r，ε，h)模型构建算法描述如下:

3 实验分析

本文设计的基于平移的数据隐藏方法(模型构建算法)由于平移方向和长度都是根据数据邻域特征动态计算和调整的，具有不可重构性，因而具有较高的数据隐私安全性.

隐藏后数据的聚类可用性采用 F-measure［13］指标进行衡量，F-measure方法将同一聚类算法作用于隐藏前后数据集，用C表示原始数据中生成的聚簇集合，Cg表示隐藏后数据集生成的聚簇集合，Ci为C中任意聚簇，Kj为Cg中任意聚簇，则

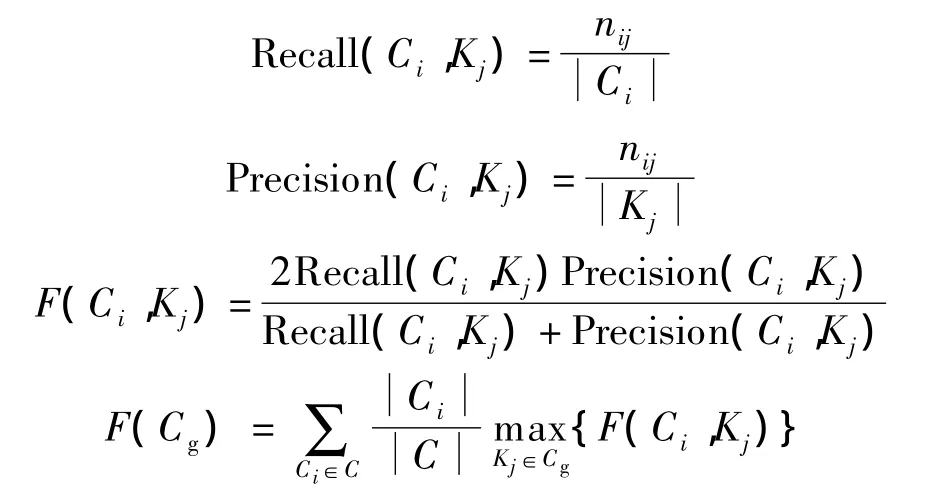
式中，Recall(Ci，Kj)和 Precision(Ci，Kj)分别描述扰动前后相应聚簇交集中数据点在Ci和Kj所占比例;F(Ci，Kj)用于衡量隐藏后聚簇Kj对原始数据聚簇Ci的聚类质量;F(Cg)用于描述隐藏前后数据集聚类质量的相似性，其值越大，表明隐藏操作对数据集的聚类可用性保持得越好.

实验平台配置如下:Intel 1.8 GHz，内存1 GB，Windows XP，用VS2008(C++)编程实现实验所涉及的算法.采用网站UCI knowledge discovery archive database(http://archive.ics.uci.edu/ml/datasets.html)的伽马望远镜数据(magic gamma telescope dataset)等进行实验.实验把基于划分的聚类算法k-means应用于隐藏前后数据集，测试F-measure值.实验中对所有原数据集过滤掉不完整记录并进行格式转换后，规范化所有数据，使它们介于(0，100)之间.

实验1对平移优化前后聚类效果进行比较.采用3个数据集测试，具体的数据集信息如表1所示.D1保留所有属性和记录，D2保留前10个数值型属性，D3随机保留10个属性和10 000条记录.

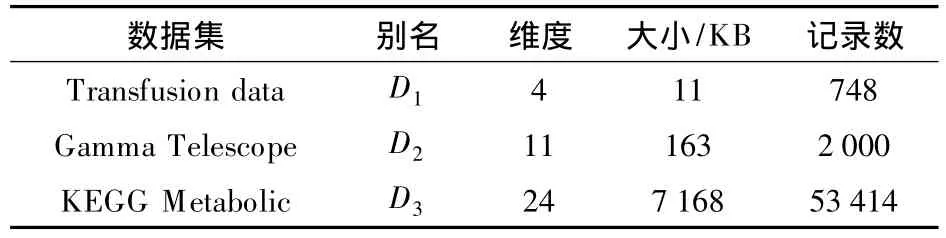
表1 实验数据信息

k-means聚类个数k=10，计算包含平均10个数据点的近邻域半径dmax，D1的dmax=136.339 0，D2的 dmax=55.567 2，D3的 dmax=31.677 1.图 7和图8中(r，ε，h)参数分别为(10，23，200)，(10，23，400)，从图中可以看出，平移优化对扰动前后聚类结果的影响较为明显，大大提高了F-measure值.因此，平移优化在一定程度上能够更好地维持聚类结果.

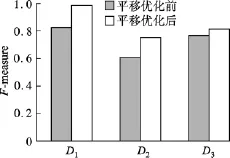
图7 平移优化前后聚类结果比较(h=200)

图8 平移优化前后聚类结果比较(h=400)

实验2测试优化后给定不同模型参数(r，ε，h)对聚类效果的影响.k-means聚类个数k=10，采用的数据集为D2.表2和表3显示了在不同的r下，各种(ε，h)的F-measure值的对比结果.实验结果表明，r取值越小、ε取值越大、h取值越小时，聚类结果维持得越好(F-measure值越高).

表2 r=10时不同(ε，h)的F-measure值对比

表3 r=20时不同(ε，h)的F-measure值对比

实验3测试优化后设置不同聚类参数k对聚类效果的影响.k-means聚类个数k分别取5，10，15，20，25，(r，ε，h)参数设为(10，25，200)，数据集采用D2.如图9所示，所得的 F-measure值都较高，且当设置不同的聚类参数时波动较小，可见PPC(r，ε，h)算法的扰动结果受聚类参数的影响不大.

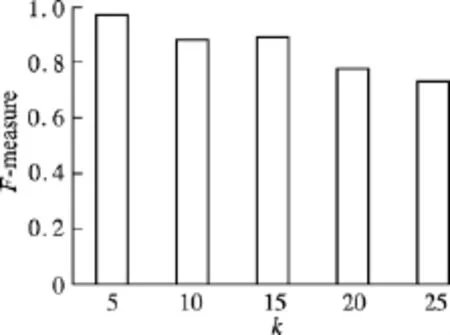
图9 统一扰动不同聚类参数的聚类效果对比

实验4分别采用 PPC(r，ε，h)，NeNDS［12］，RBT［7］和 NETPA［10］算法，对数据集 D2进行干扰前后的聚类可用性效果比较.图10为PPC(r，ε，h)算法与其他扰动方法聚类效果的对比结果，该算法与 RBT算法具有相近的 F-measure值，与NeNDS算法和NETPA算法相比，具有更高的F-measure值.因此，扰动后的数据聚类结果与原始数据聚类结果比较相似，具有较好的聚类可用性.

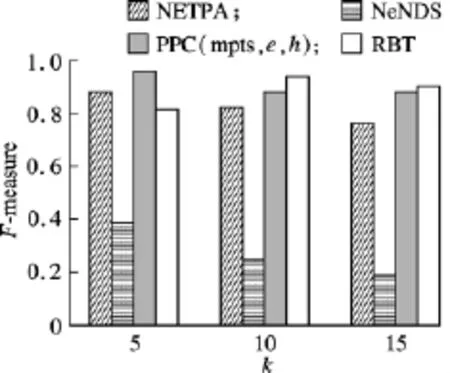
图10 PPC(r，ε，h)算法与其他扰动方法聚类效果对比

4 结语

针对面向聚类的隐私保护数据发布问题，本文提出PPC(r，ε，h)聚类隐私保护模型.该模型基于密度可达的概念，同时利用核心点的传递性平移数据点，从而避免数据点过度聚集带来的范围攻击问题.理论分析和实验结果表明，基于PPC(r，ε，h)的平移策略能有效地兼顾数据隐私安全性和发布后数据的聚类可用性.但本文没有讨论r和h的设置对模型的影响，下一步将研究参数设置以提高模型的安全性.

References)

［1］Sweeney L.k-anonymity:a model for protecting privacy［J］.International Journal on Uncertainty，Fuzziness，and Knowledge-Based Systems，2002，10(5):557-570.

［2］Machanavajjhala A，Gehrke J，Kefer D.l-diversity:privacy beyond k-anonymity［C］//Proceedings of the 22nd International Conference on Data Engineering.Atlanta，GA，USA，2006:24-35.

［3］Zhang Q，Koudas N，Srivastava D，et al.Aggregate query answering on anonymized tables［C］//Proceedings of International Conference on Data Engineering.Istanbul，Turkey，2007:116-125.

［4］Li J X，Tao Y F，Xiao X K.Preservation of proximity privacy in publishing numerical sensitive data［C］//Special Interest Group on Management of Data.Vancouver，BC，Canada，2008:473-486.

［5］Xu Y，Fung B C M，Wang K，et al.Publishing sensitive transactions for itemset utility［C］//Proc of IEEE International Conference on Data Mining.Pisa，Italy，2008:1109-1114.

［6］Oliveira S R M，Zaïane O R.Privacy preserving clustering by data transformation［C］//Proc of the 18th Brazilian Symposium on Databases.Manaus，Brazil，2003:304-318.

［7］Oliveira S R M，Zaïane O R.Achieving privacy preservation when sharing data for clustering［C］//Proc of the International Workshop on Secure Data Management in a Connected World.Toronto，Canada，2004:67-82.

［8］Oliveira S R M，Zaïane O R.Privacy preserving clustering by object similarity based representation and dimensionality reduction transformation［EB/OL］.(2004)［2011-03-05］. http://www.site.uottawa.caP ～zhizhanPppdmworkshop2004Ppaper3.pdf.

［9］Fung B C，Wang K，Wang L，et al.A framework for privacy preserving cluster analysis［C］//Proc of IEEE Int Conf on Intelligence and Security Informatics.Taipei，China，2008:46-51.

［10］倪巍伟，徐立臻，崇志宏，等.基于邻域属性熵的隐私保护数据干扰方法［J］.计算机研究与发展，2009，46(3):498-504.Ni Weiwei，Xu Lizhen，Chong Zhihong，et al.A privacy preserving data perturbation algorithm based on neighborhood entropy［J］.Journal of Computer Research and Development，2009，46(3):498-504.(in Chinese)

［11］Parameswaran R，Blough D M.Privacy preserving data obfuscation for inherently clustered data［J］.International Journal of Information and Computer Security，2008，29(1):4-26.

［12］Li X B，Sumit S.Data clustering and micro-perturbation for privacy-preserving data sharing and analysis［C］//Proc of International Conference on Information Systems.Saint Louis，MO，USA，2010:58-72.

［13］Fung B C M，Wang K，Wang L，et al.Privacy-preserving data publishing for cluster analysis［J］.Data ＆Knowledge Engineering，2009，68(6):552-575.