土体支承刚度对下沉期沉井内力的影响分析

穆保岗 肖 强 张立聪 朱建民 龚维明

(1东南大学土木工程学院，南京210096)

(2常州市武进区建设工程质量监督站，常州213159)

大型沉井的平面尺寸巨大、下沉深度深，施工控制远比中小沉井复杂.国内外学者已就沉井基础的整体稳定性、受力特性、土体的应力应变、侧摩阻力、沉井强度及变形等方面进行了大量研究［1-4］.我国在2002年和2007年制订的行业规程中，也对中小沉井施工过程的计算做出了相应规定［5-6］，但并未考虑大型沉井施工过程的特殊性.

随着我国大型沉井的成功实践［7-8］，目前沉井下沉期的研究主要集中于沉井的下沉控制，而对于沉井结构本体安全性的研究则不够深入.现行规范针对施工过程中的强度验算，规定了井壁和刃脚的计算方法，却没有明确规定内隔墙的计算方法，且未考虑施工行为对结构内力分布的影响.

为控制大型沉井的姿态，一般对刃脚内侧的土块进行保护性保留，沉井的下沉过程是由内部下沉带动刃脚的下沉，对刃脚内部附近土体一般不予开挖，因此刃脚不会出现中小沉井经常遭遇的向内或向外挠曲的极端情况.大型沉井本体安全的工程监控结果表明，开挖方式对沉井内隔墙的应力应变存在较大影响［9-10］，下沉过程中内隔墙的最大应力由竖向荷载控制.从目前我国大型沉井的工程实践情况来看，虽然大型沉井都能顺利下沉，但是在下沉过程中均遭遇到开裂困扰，仅对井壁在水平荷载下的强度进行验算是偏于不安全的［11-12］.

本文针对大型沉井的不同开挖方式，采用文克尔地基弹簧模拟下沉过程中外部井壁刃脚和内部隔墙下土体支承，计算了不同支承刚度对沉井弯矩内力的分布和数值的影响，提出了最不利计算工况，以防止沉井开裂.

1 下沉过程内力计算及分析

1.1 沉井概况

马鞍山长江公路大桥及接线工程位于安徽省东部，连接马鞍山和巢湖2市，为三塔两跨悬索桥，结构呈对称布置，2个主跨的跨度均为1 080 m，南锚碇基础采用沉井.沉井的平面尺寸为60.2 m×55.4 m，设计沉井高48 m，共分9节，布置25个井孔.第1节为8 m高钢壳混凝土沉井，其余节段为钢筋混凝土沉井，且第2节至第7节高5 m，第8节高5.5 m，第9节高4.5 m.沉井顶面标高 +4.5 m，基底标高 －43.5 m.

对该沉井而言，有大锅底开挖和小锅底开挖(又称分区开挖)2种方式可供选择(见图1).大锅底开挖是由中心向四周辐射状扩大开挖;分区开挖时，普通隔墙下土体首先被取空，分区隔墙下土体予以保留，以形成改善内力分布的支承.

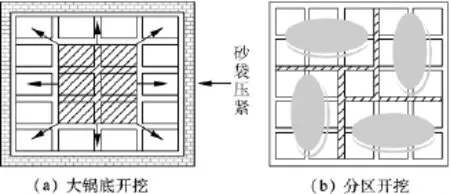
图1 开挖方式示意

普通隔墙和分区隔墙的相互关系见图2.由图可见，分区隔墙底标高稍高于四周的刃脚，低于普通隔墙.

图2 分区隔墙和普通隔墙的相对关系图

由于大型沉井的排水下沉阶段受力更为不利，故本文仅对前4节排水下沉进行分析.

1.2 计算参数

采用文克尔地基模型，将沉井视作文克尔地基上的弹性地基梁，按照弹性地基梁的有限元法对本工程沉井内力进行计算.采用SAP2000程序对弹性地基梁内力进行求解.

对沉井首次接高4节下沉进行计算时，沉井首节为钢壳混凝土，其余均为钢筋混凝土.底节钢壳采用10 mm厚的Q235B型钢板焊接而成，内部浇筑C30混凝土;其余节段钢筋混凝土等级为C30，受力钢筋型号为HRB335.隔墙水平向钢筋直径为25 mm，间距为100 mm;竖向钢筋直径为20 mm，间距为150 mm.

1.3 基床系数

基床系数K通常依照基础的实测沉降量确定［13-14］，即

式中，p0为基底平均附加压应力;sm为基础的平均沉降量.

南锚沉井在沉井顶面布置了由16个监控点组成的观测网.前4节浇筑完毕后沉井在下沉前的累积平均沉降为534 mm，自重为684.432 MN.按刃脚和隔墙底部共同支承计算可得基底平均压力为2.655 MPa，基床系数取为 4.972 MN/m3.

1.4 计算步骤和杆件编号

计算时将沉井结构简化为弹性地基梁，采用压缩弹簧模拟地基反力，每间隔1.0 m布置1个弹簧支座.根据集中变基床系数的定义，按照支承面积计算刃脚井壁处的集中基床系数 K1=9.944 MN/m，内隔墙处的集中基床系数 K2=6.960 MN/m.因沉井截面弯矩为控制内力，因此本文重点分析各种工况下的截面弯矩情况.

沉井的首次下沉计算模型简图和杆件编号(计算跨度取至中心线)分别如图3和图4所示.图4中，编号16～18，23～25，38～40，41～43的杆件为分区隔墙.编号18，23，38，43的杆件围成的中部井孔在设计阶段已预定为非开挖井孔，用以控制形成4个小锅底的分区开挖.

图3 沉井计算示意图(前4节)

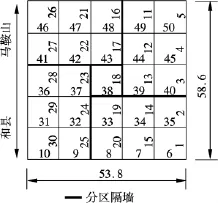
图4 杆件编号(单位:m)

2 计算结果

2.1 等支承刚度

最理想的情况是沉井下沉时严格遵循“对称取土、均匀下沉”的施工控制原则.此时认定刃脚和分区隔墙下的土体单位面积支承刚度是相等的，刃脚和分区隔墙均匀下沉.

分别对大锅底开挖和分区开挖的情况进行计算，计算条件及内力图详见图5和图6，计算结果分别列于表1和表2.由于结构的对称性，表中仅列出了一半杆件的内力结果.由表1可知，大锅底开挖工况下，井壁和内部隔墙均出现正弯矩，其中隔墙的最大弯矩出现在分区隔墙的跨中位置(即23和38号杠件处)，其次为分区隔墙和普通隔墙的交接处.

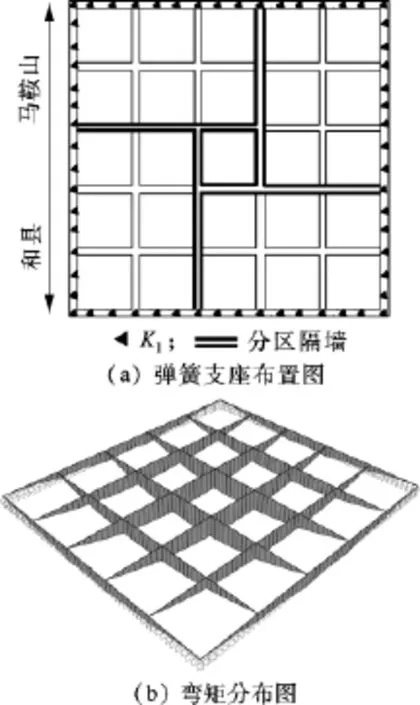
图5 大锅底开挖工况

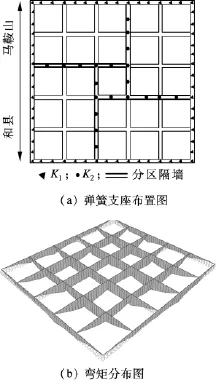
图6 分区开挖工况

由表2可知，在分区开挖工况下，由于支承条件的改善，隔墙和井壁均出现正弯矩，但弯矩均明显减小，且隔墙的弯矩分布比较均匀.分区开挖改善了沉井的内力分布，相对于大开挖而言，分区开挖使隔墙的弯矩处于较小的水平，后者隔墙的最大弯矩约为前者的36%.

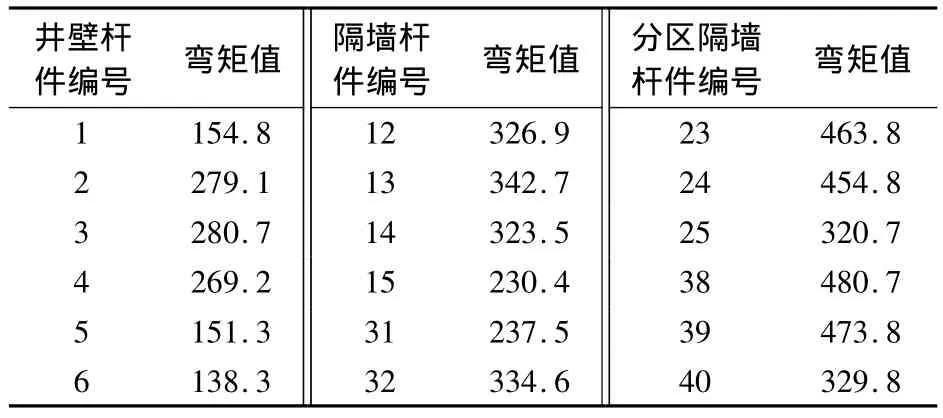
表1 大锅底开挖的计算结果 MN·m

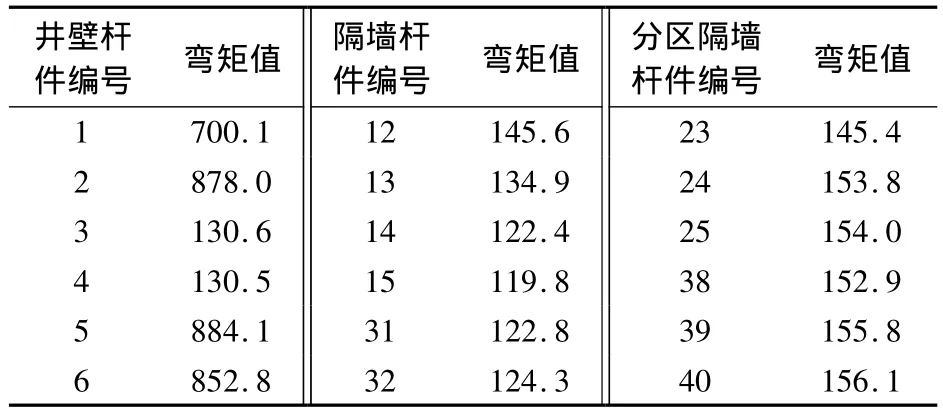
表2 分区开挖的计算结果 MN·m

因此，同等条件下采取分区开挖的方式进行施工，构件的内力会处于更低水平，有利于防止裂缝的产生.

2.2 考虑刚度比变化的分区开挖

刃脚和内部分区隔墙下的保留土体形成弹性支座.支座本身随沉井的下沉而下沉，下沉过程中刃脚和内部分区隔墙下的保留土体支承情况较复杂，会反复出现压实—扰动—再压实的情况，沉井下均匀取土的理想状态难以实现.取土的不均匀性，通常会导致以下2种工况:① 刃脚受到扰动，导致刃脚处支承刚度K1降低;②分区隔墙取土过快，导致分区隔墙下支承刚度K2降低.

2.2.1 K1值降低后的计算结果

实际工况中无法准确量化刃脚支承刚度的降低程度，计算时需假定分区隔墙支承刚度K2不变，同时刃脚下支承刚度K1依次降低25%，50%，75%，所得的弯矩分布如图7所示.

图7 刃脚支承刚度降低时的弯矩分布

由图7可知，弯矩的分布特征如下:

1)分区隔墙相当于普通隔墙的支座，普通隔墙呈现连续梁的受力特征;普通隔墙与分区隔墙相交处的支座均表现为顶部受拉的负弯矩特征.

2)分区隔墙所形成的中间井孔顶部均承受负弯矩，相邻跨则底部受拉.

3)井壁的弯矩分布是正、负相间的，弯矩水平远低于内部普通隔墙.

4)刃脚支承刚度持续降低时，分区隔墙所形成的中间井孔的负弯矩明显增长，相邻跨的正弯矩随之减小.在此工况下，普通隔墙的底部正弯矩和中间井孔顶部的负弯矩为控制内力.

表3列出了K1分别减少50%和75%时部分隔墙的弯矩值.由表可知，与分区隔墙相邻的普通隔墙弯矩值由底部受拉变为顶部受拉，内力绝对值增加200%以上.

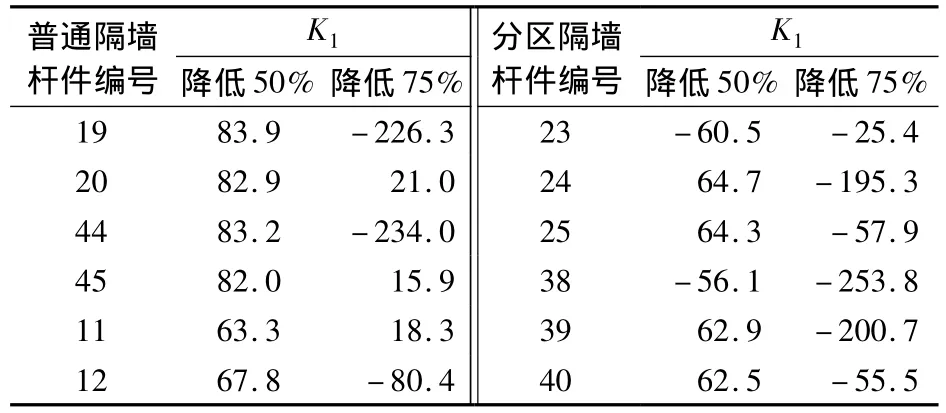
表3 K1值降低后的弯矩值计算结果 MN·m

分区隔墙支承刚度降低的极限状况是刃脚下无支承(即K1=0)，此时的弯矩分布图如图8所示.在极限情况下，普通隔墙和分区隔墙的弯矩均为负弯矩，内部隔墙的受力类似于悬臂结构，支座为分区隔墙所形成的中间井孔.由于沉井姿态施工控制的原因，大型沉井刃脚不会处于无约束的自由状态，即在分区开挖时不会出现此种工况.因此，建议以K1初始值减少50%作为内隔墙顶部负弯矩的控制工况.

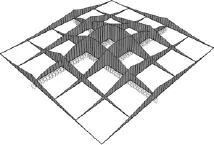
图8 K1=0时的弯矩分布

2.2.2 K2值降低后的计算结果

当刃脚下支承刚度K1维持不变，K2分别降低25%，50%，75%时，隔墙的内力计算结果见表4.此时，弯矩分布图形态均类似于大锅底开挖的情形.

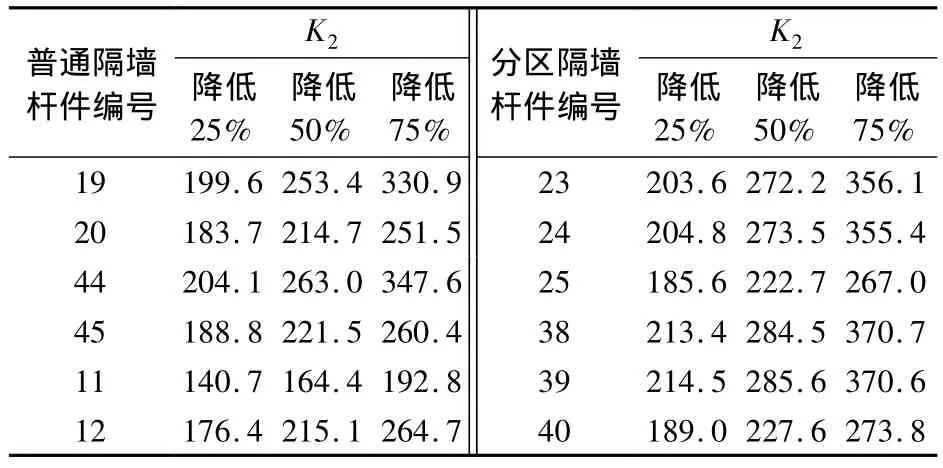
表4 K2值降低后的弯矩值计算结果 MN·m

由表4可知，随着内部分区隔墙支承刚度的降低，隔墙的正弯矩均逐渐增大.分区隔墙支承刚度降低的极限情况是隔墙下无支承(K2=0)，形成实质上的大锅底开挖.

分区开挖时分区隔墙下土体受到扰动的情况出现频率较高.表4的结果充分说明了控制分区隔墙下土体支承刚度的重要性.

2.3 计算结果讨论

进一步计算表明，决定隔墙弯矩分布和数值大小的是支承刚度比K1/K2，而非支承刚度的绝对值.图9(a)为顺桥向中间1道隔墙的弯矩分布随刚度比变化的趋势.由图可知，K1/K2值的变化对分区隔墙的弯矩分布和数值影响明显，特别是在减小K1时，内力变化剧烈.

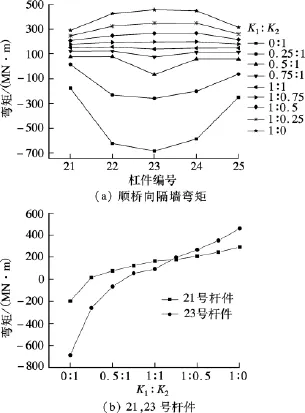
图9 隔墙弯矩随K1/K2变化曲线

在K1，K2均不折减的情况下，隔墙的内力值最为均匀.图9(b)为21，23号杆件的隔墙弯矩值随K1/K2变化的情况.

上述分析均建立在理想状态下.实际上，沉井排水下沉的过程中，下沉操作一般采用真空泵吸取混合泥浆的方式排土，无法精确控制刃脚和内部隔墙的支承刚度.因此，K1/K2很难维持在恒定状态，施工过程中隔墙内力波动较大.工况控制应当遵循危险状态，即底部弯矩应由大锅底开挖状态控制，顶部弯矩按照初始刃脚支承刚度减少50%来控制.

马鞍山南锚沉井内隔墙2个方向的跨度分别为53.8 和58.6 m，跨高比分别为 2.39 和2.60，属于深受弯构件.弹性力学中均布荷载的简支深梁应力计算公式为［15］

式中，σx为弯曲应力;M为截面弯矩;I为截面惯性矩;y为在y轴方向上截面中心至计算点的距离;q为均布荷载;b为截面宽度;h为截面高度.

按照大锅底开挖方式，根据式(2)计算隔墙底部应力.普通隔墙下最大应力值为199.56 MPa，相应的应变值约为9.68×10－4;分区隔墙下的最大应力值为185.1 MPa，相应的应变值约为8.98×10－4.

3 工程实测

在马鞍山南锚的下沉过程中，对沉井本体的应力应变进行了全程监控.应变监控仪器所用钢板计为南瑞 NVGS-150振弦式应变计，量程为 3×10－3，设置于首节钢壳沉井底部的10 mm厚钢板底部;警戒值取设计强度的80%，即168 MPa，对应的应变约为8×10－4.按照预先分析，该沉井底部抗弯能力较弱，应采用分区开挖的模式;当构成实质性大锅底时，部分构件应变值将处于警戒值以上.

按照大锅底开挖进行的仪器布置图见图10.中部仪器分布较密，周边仪器数量较少.

图10 首节钢壳沉井钢板应变计布置图

3.1 普通隔墙下的实测数据

顺桥向的普通隔墙下监测仪器编号分别为111～113和141～143.普通隔墙下钢板计的实测应变值见图11.在完全理想状况下，编号111与143，112与142，113与141的仪器观测值应该是相等的，2道普通隔墙下的实测应变曲线存在相似关系，但数值不等，各有1处仪器读数一直为负数.这说明即使按照预定的分区方式开挖，分区隔墙对普通隔墙并没有形成有效的支承.

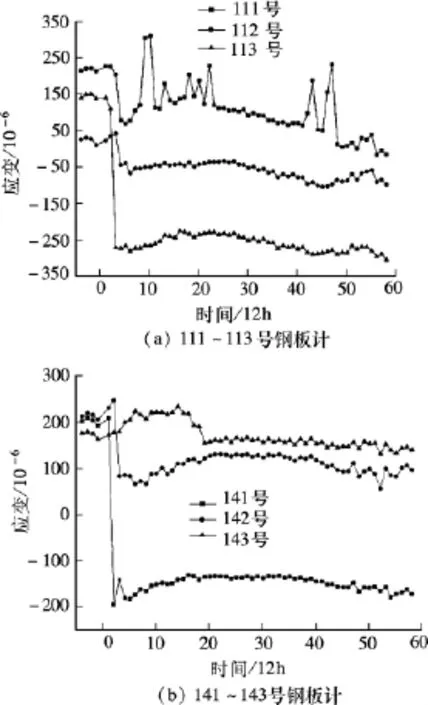
图11 普通隔墙下钢板计的应变值

3.2 中部隔墙(含分区隔墙)下的实测数据

顺桥向2道中隔墙下的监测仪器编号分别为121～129和131～139.顺桥向中部隔墙钢板计的应变值详见图12.在分区开挖时，内力应该是对称相等的.但2道隔墙下的应变值相差较大，说明2道隔墙下支承刚度不同.其中，位于分区隔墙下124和125号钢板计的应变值一直维持在1.5×10－4～2.5 ×10－4之间，分区隔墙底部呈现受拉特征，说明其底部弹性支承有向下的挠曲变形，支承刚度有限.而位置靠近普通隔墙和分区隔墙交界处的122，123号钢板计的观测值波动较大，这是由于下沉过程中支承刚度不断动态变化所致.

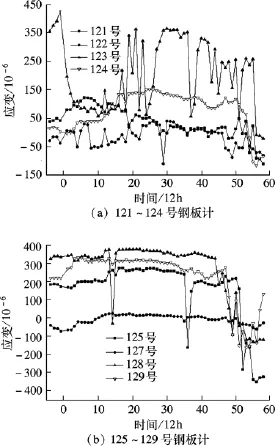
图12 顺桥向中部隔墙下钢板计的观测值

横桥向2道中部隔墙下钢板计的观测数值比较符合对称规律(见图13).由图可知，隔墙的应变观测值变化趋势为上升—平稳—下降，符合沉井的工序特征.实测数据的波动性较大，说明沉井的实际支承状态处于较为复杂的情形，是各种理论工况的复杂耦合.沉井在设计和施工时按照分区开挖方式进行计算，但由于分区隔墙的实际支承刚度是有限的，且受下沉过程的扰动呈现动态变化，构成实质上的大锅底受力状态，因而使得沉井处于不安全状态.

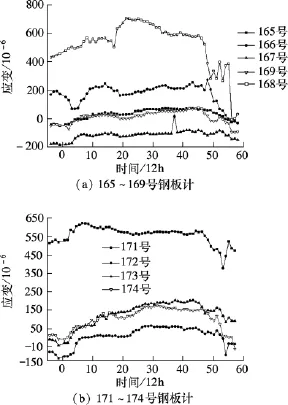
图13 横桥向中部隔墙下钢板计的观测值

4 结论

通过对马鞍山大桥南锚碇沉井进行的理论分析以及与实测数据的对比研究发现，均匀取土下沉时，与大锅底开挖方式相比，分区开挖可以明显减小沉井内部隔墙的弯矩峰值.分区开挖时，刃脚和分区隔墙下的支承刚度比显著影响沉井的内力分布.应以大锅底的极限状态来控制内部隔墙的底部正弯矩，以刃脚下K1值降低50%来控制内隔墙顶部负弯矩.实测结果表明，即使按照分区开挖控制，其内部分区隔墙下土体实际支承刚度仍然有限且不均匀.

现有的大型桥梁实践已经证明，大型沉井本体在下沉过程中会遭遇比运营阶段更加危险的最不利工况，因而也是制约其应用的技术瓶颈.本文的分析结论可为大型沉井的设计与施工控制提供技术依据.

References)

［1］Hogervorst J R.Field trials with large diameter suction piles［C］//Proceedings of the 12th Annual Offshore Technology Conference.Houston，Texas，USA，1980:217-224.

［2］Tjelta T I，Guttormsen T R，Hermstad J.Large-scale penetration test at a deepwater site［C］//Proceedings of the 18th Annual Offshore Technology Conference.Houston，Texas，USA，1986:201-212.

［3］Dyvik R，Anderson K H，Hansen S B.Field tests on anchors in clay［J］.Journal of Geotechnical Engineering，1993，119(10):1515-1531.

［4］Allenby D，Waley G，Kilburn D.Examples of open caisson sinking in Scotland［J］.Geotechnical Engineering，2009，162(1):59-70.

［5］上海市政工程设计研究院.CECS 137—2002给水排水工程钢筋混凝土沉井结构设计规程［S］.北京:中国工程建设标准化协会，2003.

［6］中华人民共和国交通运输部.JTG D63—2007公路桥涵地基与基础设计规范［S］.北京:人民交通出版社，2007.

［7］陈光福.江阴长江公路大桥特大型沉井施工述评［J］.土工基础，1999，13(3):24-28，13.Chen Guangfu.The construction of the large caisson in Jiangyin Highway Bridge［J］.Soil Engineering and Foundation，1999，13(3):24-28，13.(in Chinese)

［8］陶建山.泰州大桥南锚碇巨型沉井排水下沉施工技术［J］.铁道工程学报，2009(1):63-66.Tao Jianshan.Construction technology for drainingsinkage for south caisson anchorage to Taizhou Yangtze River Highway Bridge with large-size sunk well［J］.Journal of Railway Engineering Society，2009(1):63-66.(in Chinese)

［9］穆保岗，朱建民，牛亚洲.南京长江四桥北锚碇沉井监控方案及成果分析［J］.岩土工程学报，2011，33(2)，269-274 Mu Baogang，Zhu Jianmin，Niu Yazhou.Monitoring and analysis of north anchorage caisson of Fourth Nanjing Yangtze River Bridge［J］.Journal of Geotechnical Engineering，2011，33(2):269-274.(in Chinese)

［10］杨灿文，黄民水.某大型沉井基础关键施工过程受力分析［J］.华中科技大学学报:城市科学版，2010，27(1):17-21.Yang Canwen，Huang Minshui.Stress analysis of a large open caisson key construction process［J］.Journal of Huazhong University of Science and Technology:City Science Edition，2010，27(1):17-21.(in Chinese)

［11］Guo Zhenghong，Xu Wei.Research on the stress mechanism of the ultra-deep open caisson system during subsidence process［C］//Proceedings of the GeoShanghai Conference.Shanghai，2006:142-149.

［12］Chakrabarti S，Chakrabarti P，Sri Krishna M.Design，construction，and installation of a floating caisson used as a bridge pier［J］.Leadership and Management in Engineering，2006，132(3):143-156.

［13］黄昌乾，李国强，潘启辉.基床系数取值方法相关问题分析［J］.建筑结构，2010，40(S1):298-302.Huang Changqian，Li Guoqiang，Pan Qihui.Problems analysis related to the coefficient of subgrade［J］.Architectural Structure，2010，40(S1):298-302.(in Chinese)

［14］莫海鸿，杨小平.基础工程［M］.北京:中国建筑工业出版社，2003.

［15］徐芝纶.弹性力学［M］.3版.北京:高等教育出版社，2002.