地铁运行诱发的环境振动数值模拟与模型预测

张鹤年 阳建强 孙广俊 肖军华

(1东南大学建筑学院，南京210096)

(2南京工业大学土木工程学院，南京210009)

城市轨道交通在带给人们方便的同时，其负面影响也日益引起了人们的关注.其中，由于轨道交通运行诱发的振动对周边环境的影响问题尤为显著［1］.轨道交通的振动和噪声不但会对沿线居民的生活造成影响，而且会引起周围岩土介质及沿线结构物的破坏［2-5］.因此，研究城市轨道交通对周边环境振动的影响及控制，对提高城市轨道交通系统的规划、设计和运营水平，保证工程结构的安全，改善城市环境质量，提高居民生活质量等方面具有重要的理论意义和社会效益.国内外针对城市轨道交通列车振动对环境的影响研究，主要有解析、数值和实验方法.在数值计算方面，分为整体分析法和子结构法［6-7］.整体分析法即建立列车-轨道-周围环境的整体模型，以轮轨不平顺为系统激励，模拟求解运动车辆对周围环境的振动影响.而子结构法将这类问题分为对振源问题的研究和对受振系统的相应研究，即在首先明确列车动荷载作用机理基础上，以此荷载作为受振系统的激励力，对环境系统的振动传播规律进行模拟和计算.

本文基于轮轨不平顺原理建立了列车荷载的激励函数表达式，采用有限元技术模拟了隧道-轨道-道床振动传播路径，对地铁运行引起的环境振动进行了数值求解，并与作者已发表的实测数据进行了对比验证［8］，分析了地铁运行诱发环境振动的参数影响规律，通过统计回归建立了地铁运行对周边环境振动影响的预测模型.

1 环境振动数值分析模型

1.1 列车荷载模拟

由于轨道不平顺是车辆和轨道系统振动的主要激励源，影响轮轨力的主要原因在于轨道不平顺和轨面波形磨耗效应.研究表明［9］，竖向轮轨力主要出现在3个频率范围内:低频部分为0.5～10 Hz，几乎全部由车体对悬吊部分的相对运行而产生;中频部分为30～60 Hz，由簧下轮对质量对钢轨的回弹作用而产生;高频部分为100～400 Hz，由钢轨在运行时受到轮轨接触面的抵抗而产生.因此，可以用一个激振力函数来模拟列车的随机振动荷载［9］，其中包括静力荷载和由一系列正弦函数叠加而形成的动力荷载.

基于轨道不平顺原理，采用与高、中、低频振动，附加动荷载以及轨道波磨效应相对应的激振力来模拟轮轨之间的相互作用，即轨道交通荷载，可以表示为

式中，P0为车轮静荷载;P1，P2和P3分别为对应于Ⅰ，Ⅱ，Ⅲ控制标准中的某一典型值的振动荷载，如表1所示;ωi为相应车速下相应于Ⅰ，Ⅱ，Ⅲ控制标准下不平顺振动波长的圆频率.

假设列车簧下轮对质量为M0，则相应的振动荷载幅值为

表1 轨道几何不平顺值

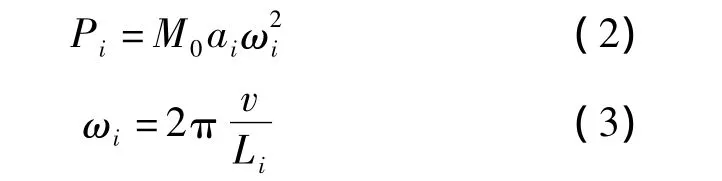
式中，v为列车的运行速度;ai，Li分别为相应于Ⅰ，Ⅱ，Ⅲ控制标准下的矢高和典型波长.

1.2 轨道支承结构-地基土有限元模型

轨道支承结构可以定义为地基土上用来传递振源模型输出的动力荷载的结构，地下线路的轨道支承结构则为隧道结构.由于地下线路的荷载作用在钢轨上，因此将钢轨、整体道床和隧道衬砌合为一体，统一定义为隧道结构，以此作为地铁的轨道支承结构.

地铁运行引起的环境振动主要指线路周围地面和建筑物的振动，所以有限元建模时必须充分考虑振动的传播特点，适当设置模型尺寸、网格大小、边界条件、材料参数等条件.

本文将轨道支承结构与地基土的接触定义为直接绑定接触，忽略基础与周围土层之间的接触非线性，并且由于振动荷载在土壤中产生的应变较小，因此土体可以近似按弹性介质考虑.地下线路系统模型尺寸为120 m×70 m×60 m，如图1所示.地铁隧道结构的三维有限元模型如图2所示，建模时假定地下线路的截面沿线路方向保持不变，单元类型采用SOLID45，并对模型进行自由网格划分.

图1 地铁隧道-地基土振动传播路径模型

由于涉及到土体的有限元计算模型不可能取无限大的区域来计算，因此只能截取其中一部分来分析动力问题.由于在截取的边界面上会发生波的反射，不能真实模拟无限地基，而给计算结果带来不容忽视的误差，因此需要设置人工边界条件以消除人为边界对计算的影响.本文采用三维时域黏弹性人工边界作为地基土的边界条件［5］，即在模型边界土层单元节点的法向和切向上均设置弹簧和黏性阻尼器，其具体实施方法如图3所示.

图2 地铁隧道结构模型

图3 三维黏弹性人工边界示意图

图3中，坐标x，y沿人工边界的切向，z为法向，图中黏弹性人工边界节点上物理元件的参数为

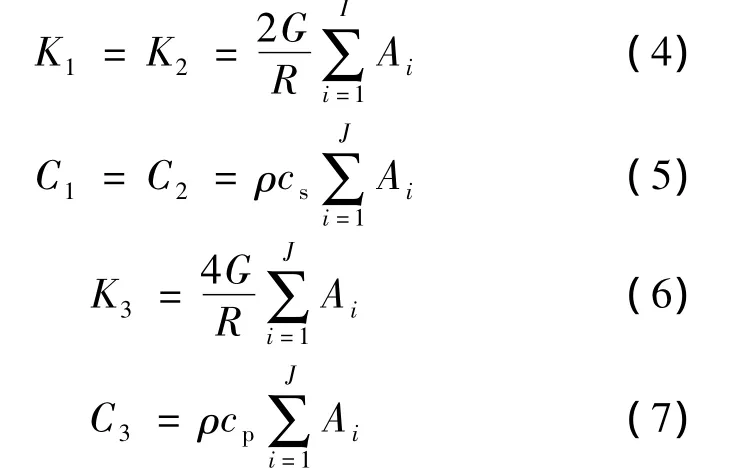
式中，Ki和Ci分别为弹簧和阻尼器参数;G为介质等效剪切模量;为介质边界节点所表示的面积;cs和cp分别为介质等效纵波和横波波速;R为波源至边界节点的距离;ρ为介质质量密度;J为单元数.

2 环境振动数值模拟

本文针对南京地铁1号线小行站至中胜站区间地铁诱发的环境振动进行数值模拟，并将模拟结果与作者在该区间实测的地铁振动进行比较［8］.数值模拟的参数选取如下:

1)列车参数 采用一个激振力函数来模拟列车振动荷载.根据文献［10］轮轨相互作用的实测结果和式(1)～(3)，在确定参数 ω，P0，P1，P2，P3后，可分别得到机车和客车轮轨接触荷载为:①机车FJ= －70 －5.181sin314t－9.4sin691t－19.6sint;② 客车 Fk= －77.5 －5.1sin314t－9.4sin691t－19.6sint.

3)地基土参数 在模型中假设地基土是不分层的单一土体，地基土属性为粉质黏土，卓越周期为0.55 s，弹性模量为 15 MPa，密度为 1.9 ×103kg/m3，泊松比为 0.325，阻尼比为 0.15.

计算地面测点与轨道中心线距离d'分别为5，10，20，40，60，80 m 的竖向加速度时程，如图 4 所示.

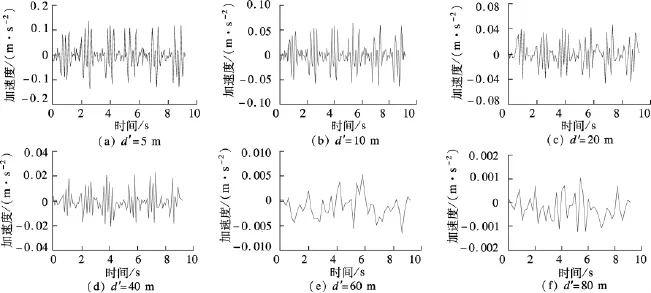
图4 地面不同距离位置的竖向加速度时程

本文取距离振源5 m处的模拟加速度和现场实测数据进行对比，如图5所示.此外，将模拟计算的振级与实测值进行比较，如图6所示.

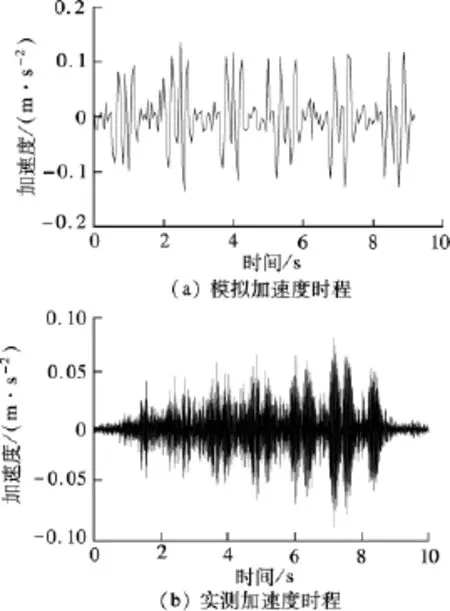
图5 模拟加速度时程与实测值对比

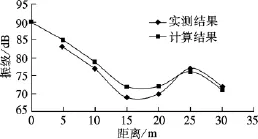
图6 模拟振级与实测值对比

由图5和图6可以看出，振动波形、幅值和振级等主要指标的数值模拟结果与实测结果基本一致，模拟的振幅稍大于实测的结果.由于模拟和实测的采样频率不同，因此导致两者的图形在形式上略有差别.这表明基于有限元建模分析得出的计算结果能够较为真实地反映地铁运行引起的环境振动的实际情况.

3 环境振动参数影响分析

为了进一步揭示轨道交通参数对环境振动的影响，分别对不同列车速度、地基土性质和隧道埋深情况下的环境振动反应进行分析计算.

图7为其他参数均保持不变，仅改变列车速度v情况下，地面不同位置的竖向振动振级衰减曲线.

由图7可以看出，随着列车速度增加，地面竖向加速度振动呈增大趋势.距离轨道交通线路较近处，速度对地面振动的影响差别小于距离轨道交通线路较远处速度对地面振动的影响差别.这与其他学者研究较多的普通铁路、高速铁路列车速度对环境振动的影响情况相同［11］.

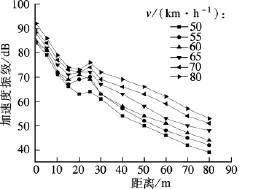
图7 列车速度变化引起的地面振动振级衰减曲线

图8为其他参数保持不变，不同地基土卓越周期T时，地面不同位置的竖向振动振级衰减曲线.

由图8可以看出，地基土的卓越周期越大，振动在地基中的衰减越快.且卓越周期越大，列车引起的地面振动越小.

图9为其他参数均保持不变，仅改变隧道埋深h时，地面不同位置的竖向振动振级衰减曲线.

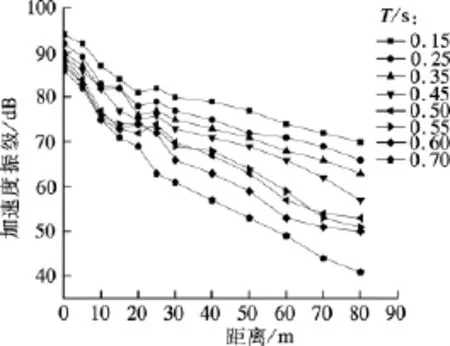
图8 地基土性质变化引起的地面振动振级衰减曲线

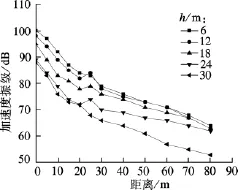
图9 隧道埋深变化引起的地面振动振级衰减曲线

4 环境振动预测模型

根据环境振动单参数分析的结果，并以本文算例中的参数取值为标准参数，综合考虑受振点距离、地基土性质、列车速度和隧道埋深等因素，建立多参数影响下的振动预测模型.

根据北京交通大学夏禾及其课题组的研究［5］(以下简称“北交大公式”)，地铁运行引起的地面振动随距离和地基土性质的变化关系为

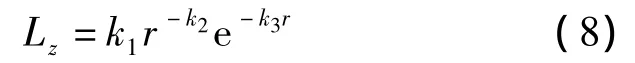
式中，Lz为地面振级;r为距离振源的距离;k1为关于振动幅值的待定系数;k2为反映几何阻尼的系数;k3为反映材料阻尼的系数.其中，k1，k2和k3与地基土性质有关.

通过对本文不同地基土条件下地面振动水平的回归分析，可以得到相应的k1，k2和k3值，再通过k1，k2和k3与相关地基土参数的回归分析，可以得到标准参数输入时不同地基土、不同距离情况下的地面振级的预测公式为

式中，ρ，μ和ξ分别为地基土密度、泊松比和阻尼比.

当改变列车速度，而其他参数均不变时所引起的地面振动与标准列车速度引起的地面振动有一个差值，它是列车速度和距离的函数.与以往的理论分析和实测分析结论相同，轨道交通列车引起的地面振动一般随列车速度的增加而增大.采用复合回归的方法建立地面振级差值Yv与列车速度v和距离r的函数关系，即列车速度的修正项为

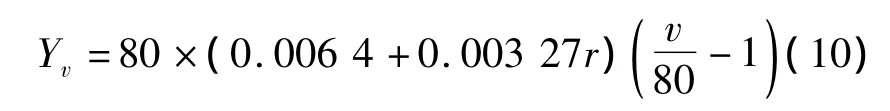
取不同隧道埋深时引起的地面振动与标准参数输入时列车运行引起的地面振动的差值为因变量，隧道埋深为自变量，回归分析其关系，可以得到隧道埋深的修正项为

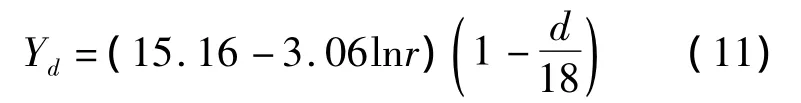
式中，Yd为振级差值;d为隧道埋深.

综合上述影响关系，最终可以得到预测公式为

在实际对地面振动预测的过程中，式(12)不易应用，故需建立简化的预测公式.公式中只保留地基土性质，并以地基土卓越周期T为变量，建立的预测模型为

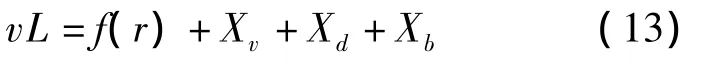
式中

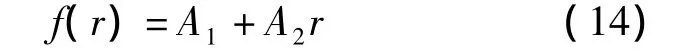
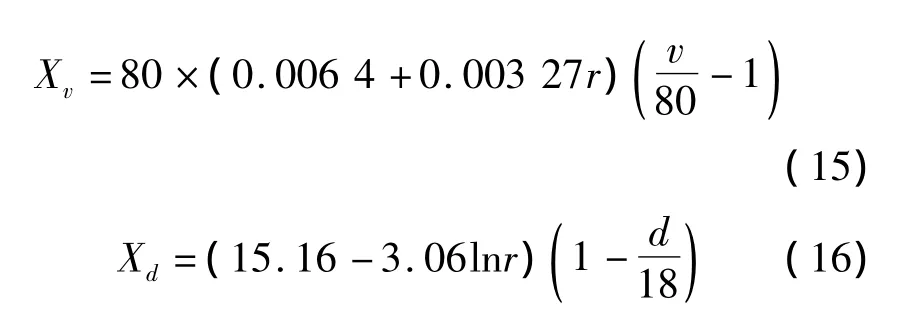
式中，f(r)为自由地面振动随距离衰减基准曲线;A1=72.3 －7.2lnT，A2=0.067 －0.426T 为地基土卓越周期T的函数;Xv为列车速度修正项;Xd为隧道埋深修正项;Xb为列车编组，取值设为0.

为了验证简化预测模型的效果，采用南京地铁地下线路中胜站的实测结果［8］，列车速度取为65 km/h，土的卓越周期取为0.15 s，隧道埋深取为14 m，将上述参数代入到本文的预测模型［13］中进行计算，并与实测结果进行对比，结果如图10所示.

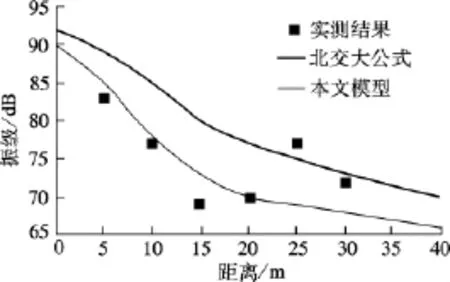
图10 预测模型与实测结果对比

可以看出，本文在“北交大公式”基础上重新进行修正后，所得的模型与北交大公式结果相比更加准确，在距离轨道中心前20 m的范围内，实测结果与计算模型的结果基本一致，振级差值在5 dB之内;在20～30 m的范围内，计算模型比实测结果小，最大差值不超过10 dB，这是由于轨道交通引起的环境振动随距离变化在某一位置存在放大现象，但基于函数构造的预测模型并不能很好地预测到放大的结果.

5 结论

1)基于轨道不平顺原理，采用一个与高、中、低频振动，附加动载和轨面波形磨耗效应相对应的激振力函数模拟地铁列车振动荷载，建立了钢轨-道床-隧道衬砌地铁轨道支承结构模型和地铁隧道-地基土振动传播模型.对地铁运行引起的环境振动进行了数值模拟，通过与实测结果的比较，表明本文的数值模拟能够较为真实地反映地铁运行引起的环境振动的实际情况.

2)随着列车速度增加，地铁运行引起的地面竖向振动加速度增大，且距离地铁线路较远，速度的影响越显著.随着与地铁线路的距离增大、地基土的卓越周期增大或隧道埋深增加，地铁运行引起的地面竖向振动加速度均减小，且地基土的卓越周期越大，振动在地基中的衰减更快.

3)综合考虑受振点距离、地基土性质、列车速度和隧道埋深，建立了多因素影响下的地面振动预测简化公式.通过与实测结果的对比，表明本文修正后的预测模型更加准确.

References)

［1］刘维宁，夏禾，郭文军.地铁列车振动的环境响应［J］.岩石力学与工程学报，1996，15(增刊):586-593.Liu Weining，Xia He，Guo Wenjun.Study of vibration effects of underground trains on surrounding environments［J］.Chinese Journal of Rock Mechanics and Engineering，1996，15(S1):586-593.(in Chinese)

［2］Bata M.Effects on buildings of vibrations caused by traffic［J］.Building Science，1971，6(4):221-246.

［3］Krylov V V.Generation of ground vibration by superfast trains［J］.Applied Acoustics，1995，44(2):149-164.

［4］Forrest J A，Hunt H E M.Ground vibration generated by trains in underground tunnels［J］.Journal of Sound and Vibration，2006，294(4/5):706-736.

［5］夏禾.交通环境振动工程［M］.北京:科学出版社，2010.

［6］Fiala P，Degrande G，Augusztinovicz F.Numerical modelling of ground-borne noise and vibration in buildings due to surface rail traffic［J］.Journal of Sound and Vibration，2007，301(3/4/5):718-738.

［7］Lombaert G，Degrande G.Ground-borne vibration due to static and dynamic axle loads of Inter City and highspeed trains［J］.Journal of Sound and Vibration，2009，319(3/4/5):1036-1066.

［8］孙麒云，张鹤年.城市轨道交通引起的地面振动实测与分析［J］.铁道标准设计，2011(7):98-100.Sun Qiyun，Zhang Henian.Site tests and analysis on ground vibration caused by urban mass transit［J］.Railway Standard Design，2011(7):98-100.(in Chinese)

［9］梁波，蔡英.不平顺条件下高速铁路路基的动力分析［J］.铁道学报，1999，21(2):84-88.Liang Bo，Cai Ying.Dynamic analysis on subgrade of high speed railways in geometric irregular condition［J］.Journal of The China Railway Society，1999，21(2):84-88.(in Chinese)

［10］周彪，谢雄耀，李永盛，等.基于地铁隧道的列车振动荷载确定方法研究［C］//海峡两岸轨道交通建设与环境工程高级技术论坛.北京:人民交通出版社，2008:373-378.Zhou Biao，Xie Xiongyao，Li Yongsheng，et al.Calculation method of train vibration loading based on subway tunnel［C］//Rail Transit Construction and Environmental Engineering Symposium in Chinese Mainland and Taiwan.Beijing:China Communications Press，2008:373-378.(in Chinese)

［11］陈建国，夏禾，肖军华，等.列车运行对周围地面振动影响的试验研究［J］.岩土力学，2008，29(11):3113-3118.Chen Jianguo，Xia He，Xiao Junhua，et al.Experimental study of ground vibrations induced by moving train［J］.Rock and Soil Mechanics，2008，29(11):3113-3118.(in Chinese)