稳态与非稳态下旋风分离器气相流场数值模拟方法研究
赵 通,杨亚平,刘俊龙
(东南大学 能源与环境学院,南京210096)
旋风分离器是工业中广泛应用的一种除尘设备,具有造价低、结构简单以及分离效率高等优点.目前,针对旋风分离器气相流场的研究方法有试验和数值模拟两种.鉴于旋风分离器内部流场的复杂性和试验方法的局限性,试验得出的结论只适用于对应的试验范围,并且试验研究需要大量的时间和高昂的成本.近年来,随着计算流体力学(CFD)技术的发展,采用数值模拟方法来模拟旋风分离器内部流场和计算分离效率成为可能.湍流模型包括标准k-e模型[1]、RNGk-ε模型[2-3]、代数应力方程模型(ASM)[4]、雷诺应力方程模型(RSM)[5-7]、大涡模拟方法(LES)[8-9]以及雷诺平均数值模拟(RANS)方法[10].根据以往学者的研究结果可以得出[11-14]:由于雷诺应力方程模型考虑了湍流的各向异性,可以很好地预测旋风分离器内部的强制涡和外部的准自由涡,因此模拟结果与试验值也最吻合.对于压力梯度项离散,采用Presto格式进行插补,压力-速度耦合采用Simplec算法是最优化的选择[15-17];对于动量方程、湍动能和耗散率项的离散,以往主要通过控制差分格式的精度进行研究,但是得到的研究结果并不一致,而且目前只能确定一阶迎风格式(FOU),由于其精度较低,因此该方法不适合用于旋风分离器内部的强旋流[13,18].大多数学者的研究表明:具有高精度的Quick差分格式最适合用于旋风分离器内部的强旋流[18-20].Quick格式具有2 阶以上精度的截差,但其极难收敛,且对网格质量要求极高,计算时间也较长.最近有学者提出,对动量方程、湍动能和耗散率项采用二阶精度二阶迎风差分格式(SOU),对雷诺应力项采用一阶迎风差分(FOU)进行离散可以很好地预测旋风分离器内部的流场.通过对其预测结果与采用Quick差分进行离散的结果以及试验数据进行对比可知:前者与试验数值更吻合[20];另外,有学者提出,对动量方程采用Quick离散,对湍动能和耗散率采用二阶迎风格式(SOU)离散得到的结果与试验值最吻合[19].过去,学者对旋风分离器气相流场的研究大多集中在采用不同湍流模型,而对控制方程的离散格式并没有进行过系统的研究,因此,笔者在稳态和非稳态下采用RSM 模型,分别对动量方程、湍动能和耗散率项采用6种不同的差分组合格式进行离散,进而对旋风分离器气相流场进行数值模拟并与试验数据进行了比较,归纳出旋风分离器气相流场数值模拟的最优化模型.
1 计算模型
对于旋风分离器内部流场的模拟,很多学者采用稳态方法[10-11]并认为旋风分离器有明确的进出口边界条件,而且认为在稳态下可以大大缩短计算时间.随着计算机处理能力的增强,对于旋风分离器内部强旋流湍流场,有学者提出在非稳态下[16-17,19]进行模拟更能符合旋风分离器内部流场的流动情况,因此笔者确定在稳态和非稳态下对旋风分离器进行模拟.图1为旋风分离器几何结构及其计算网格.

图1 旋风分离器几何结构及其计算网格Fig.1 Structure and grid of the cyclone separator
假定在旋风分离器内进行一个等温、不可压缩过程.采用软件Fluent 6.3.26 对旋风分离器气相流场进行模拟,对湍流模型采用雷诺应力方程模型(RSM),对压力梯度项采用Presto格式离散,而对压力-速度耦合则采用Simplec算法,6种不同的离散差分格式组合见表1.
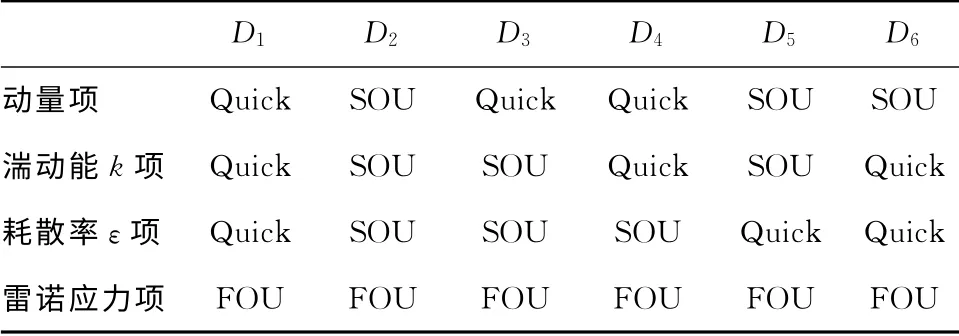
表1 6种不同的离散格式组合Tab.1 Six different combinations of discretization schemes
2 网格划分与边界条件
2.1 网格划分
本文计算采用的物理模型和结构尺寸与文献[20]中的旋风分离器试验模型相同,其基本几何结构如图1(a)所示,几何参数为:a=95 mm,b=38mm,h=285 mm,B=72.5 mm,D=190 mm,De=64mm,H=760mm,s=95mm.采用Gambit 2.3.16划分网格并采用混合网格分块划分方法将旋风分离器分割为进口段、筒体、锥段以及排气管4个部分.筒体、锥体和排气管均采用六面体O 型结构网格进行划分.由于进口段不规则,故采用非结构网格进行划分,网格总数为76 760,网格划分结果见图1(b).
2.2 边界条件
计算的边界条件为:
(1)入口边界:入口速度(Velocity_inlet)为7.5 m/s,在湍流参数的指定方法中选择湍流强度与水力直径(Intensity and hydraulic diameter),设置湍流强度为10%,水力直径为54.3mm.
(2)排气管出口:自由出流(Outflow),流量比率(Flow rate weighting)=1.
(3)排灰口:自由出流(Outflow),流量比率(Flow rate weighting)=0.
(4)排气管与筒体的公共面选用界面(Interface).
(5)固体壁面为无滑移条件,近壁采用标准壁面函数处理.
3 计算结果与分析
切向速度和轴向速度是旋风分离器内部气流的两个重要参数:切向速度使颗粒具有离心力而分离,而轴向速度则使颗粒向灰斗流动.一般认为,切向速度和轴向速度反映了旋风分离器内部气流的流动特性,因此笔者着重研究气流的切向速度和轴向速度,并将模拟值与文献[20]中的试验数据进行了对比和分析.
3.1 稳态下切向速度与轴向速度的分布
3.1.1 切向速度分布
图2为稳态下z轴径向正方向不同高度截面上切向速度的分布.从图2可知:采用RSM 可以很好地预测旋风分离器内部的切向流场,其模拟结果与试验值的趋势保持一致,且最大值的位置也基本一致,但模拟结果比试验值略高.另外,对流相采用D6离散格式得到的模拟值与试验值吻合最好.
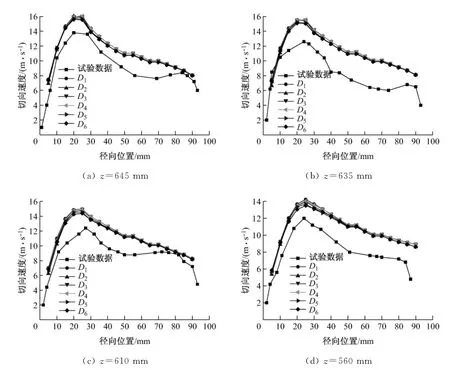
图2 稳态下z轴径向正方向不同高度截面上切向速度的分布Fig.2 Distribution of tangential velocity in steady state on sections of different heights along the zaxis
3.1.2 轴向速度分布
图3为稳态下z轴径向正方向不同高度截面上的轴向速度分布.从图3可以看出:采用RSM 可以很好地预测旋风分离器内部的轴向流场,模拟结果与试验值趋势保持一致,最大值与零点的位置基本一致,但在内部强制涡内时模拟值比试验值略高;在外部自由涡内时模拟值与试验值基本吻合,但略低于试验值.另外,对流相采用不同离散格式得到的模拟值曲线基本重合.
3.2 非稳态下切向速度与轴向速度的分布
气流停留时间(Vcyclone/Qin)为0.65s,时间步长(time step)为0.000 1s.
3.2.1 切向速度分布
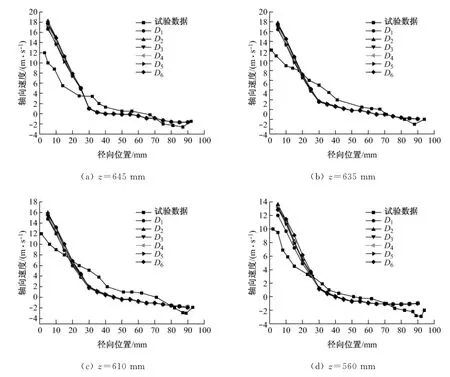
图3 稳态下z轴径向正方向不同高度截面上轴向速度的分布Fig.3 Distribution of axial velocity in steady state on sections of different heights along the zaxis

图4 非稳态下z轴径向正方向不同高度截面上切向速度的分布Fig.4 Distribution of tangential velocity in unsteady state on sections of different heights along the zaxis
图4为非稳态下不同高度上采用不同离散格式的旋风分离器内部气流切向速度模拟结果与试验值沿径向正方向的分布.从图4可以看出:采用RSM可以很好地预测旋风分离器内部的切向流场,模拟数据与试验值趋势保持一致,最大值的位置也基本一致,但模拟结果比试验值略高.在内部强制涡内,对流相采用D6离散格式得到的模拟结果与试验值最接近;在外部自由涡内,采用D1~D5离散格式的模拟结果与试验值基本重合,并且与试验值最为接近.但从总体趋势看,采用D6离散格式获得的模拟结果与试验值吻合最好.
3.2.2 轴向速度分布
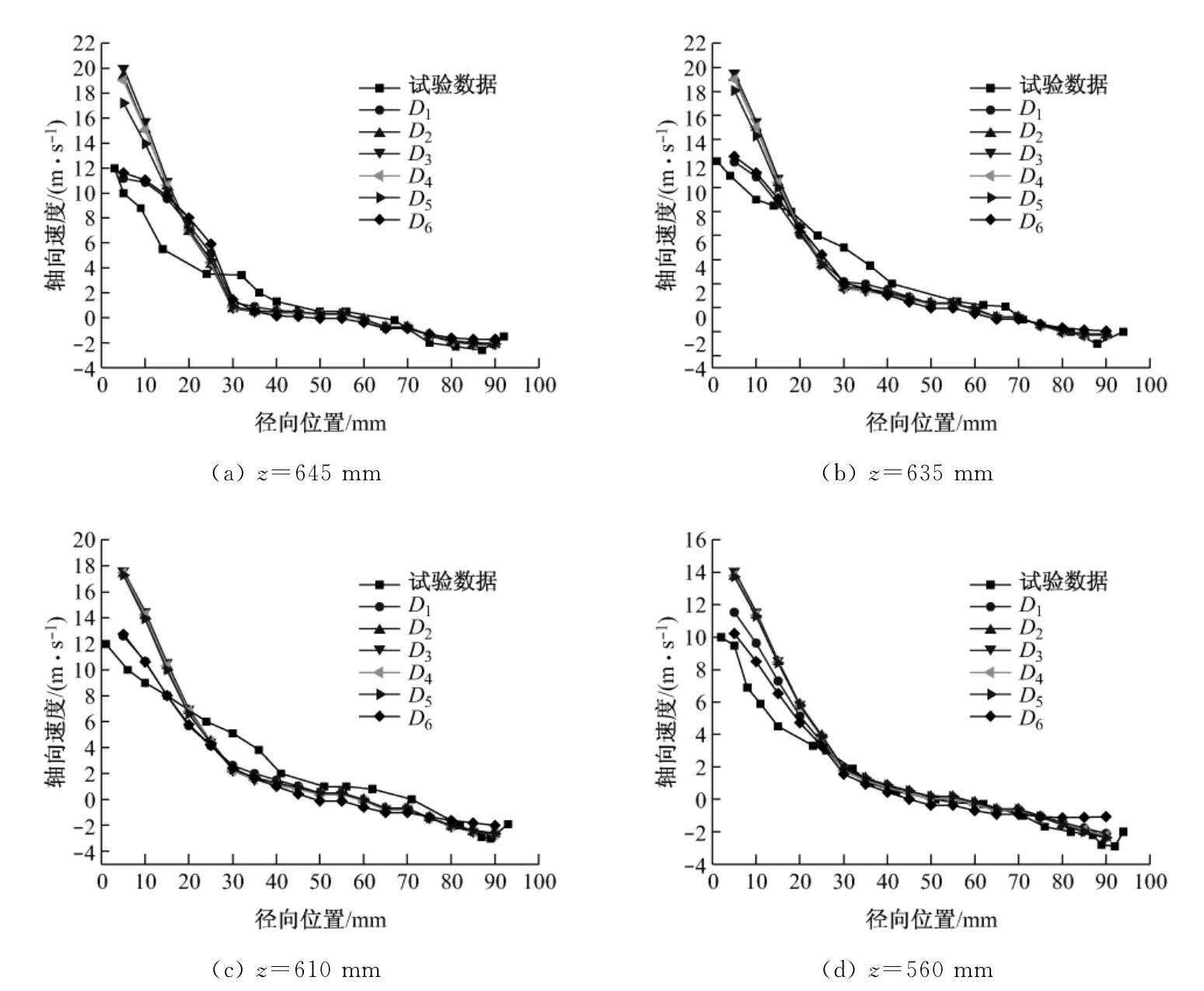
图5 非稳态下z轴径向正方向不同高度截面上轴向速度的分布Fig.5 Distribution of axial velocity in unsteady state on sections of different heights along the zaxis
图5为非稳态下z轴径向正方向不同高度截面上轴向速度的分布.从图5可以看出:采用RSM 可以很好地预测旋风分离器内部的切向流场,模拟结果与试验值趋势保持一致,最大值与零点的位置也基本一致.对旋风分离器内部流场采用D1与D6离散格式得到的模拟结果与试验值基本吻合,在外部自由涡内得到的模拟结果也与试验值基本一致.综合旋风分离器4个不同截面高度上的分布图看,采用D6离散格式得到的模拟结果与试验值最为吻合.
3.3 稳态与非稳态下速度的比较
从上面3.1和3.2节可以得出,对流场采用D6离散格式得到的模拟结果与试验值最为符合.笔者采用D6离散格式、选取圆柱段与圆锥段两个不同高度截面对稳态与非稳态下切向速度和轴向速度的模拟结果与试验值进行了比较.
图6为稳态与非稳态下z轴径向正方向不同高度截面上切向速度与轴向速度的分布.从图6可以看出:模拟结果与试验值趋势保持一致,切向速度的最大值与试验值位置基本一致,但模拟结果大于试验值;在非稳态下,轴向速度的最大值与零点位置与试验值也基本一致,且数值基本吻合.与稳态相比,非稳态下的模拟结果与试验值更加吻合.这是因为旋风分离器内部实际的气流场是强旋湍流场,湍流的一个重要特征就是随机性,即流体中的各种物理参数,如速度、压力等都随时间与空间发生随机变化,即旋风分离器内部的流场是非稳态的,只是趋向于稳态发展,因此采用非稳态下模拟的气相流场与实际的气相流场更加吻合,所以模拟得到的结果与试验测得的值也更加一致.
4 非稳态下的速度矢量图
图7为非稳态下对气相流场采用D6离散格式得到的速度矢量分布.从图7可以看到旋风分离器流场内部的准强制涡和外部的自由涡,且内涡与外涡的交界面很清晰.另外,从图7可知:气相流场在柱形空间的对称性比较好,而在锥段的对称性较差,并出现摆尾现象,这与现有文献的研究结果很符合,表明在非稳态下采用D6离散格式可以很好地预测旋风分离器内部的流场特性.
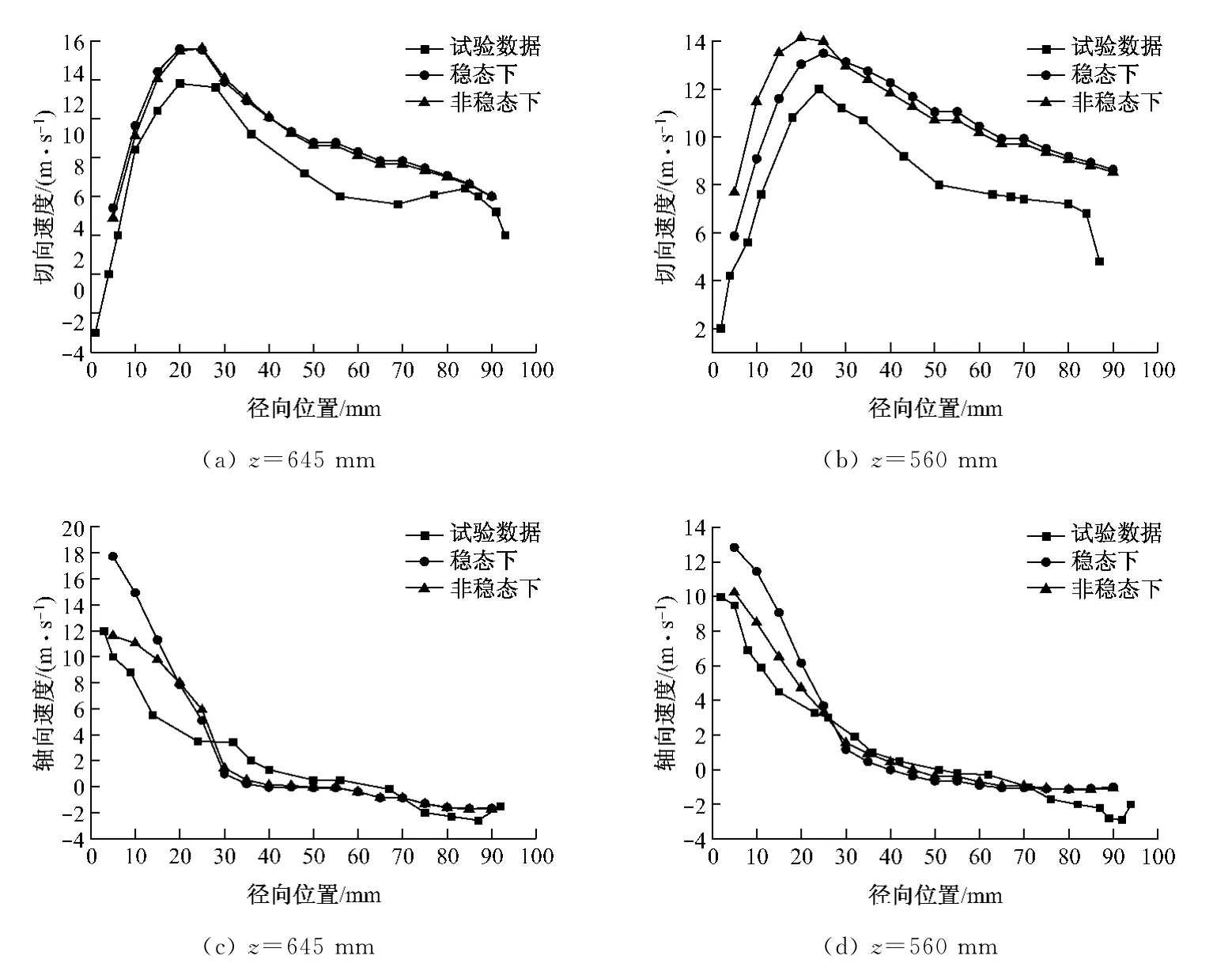
图6 在稳态和非稳态下z轴径向正方向不同高度截面上切向速度与轴向速度的分布Fig.6 Distribution of tangential and axial velocity in steady and unsteady state on sections of different heights along the zaxis
5 结 论
(1)采用雷诺应力方程模型(RSM)可以很好地预测旋风分离器内部气相流场特性.
(2)在非稳态下比在稳态下采用RSM 更能准确地模拟旋风分离器内部流场特性,从而验证了以往学者的研究结果.
(3)对于旋风分离器气相流场的模拟,其中有关湍流模型的研究已经相当成熟,目前的最佳选择是RSM.对于控制方程离散格式选择的研究尚较少,笔者通过对动量方程、湍动能和耗散率项采用6种不同的差分格式组合进行模拟比较后得出:在非稳态下,对湍流模型采用RSM,对动量方程采用两阶迎风格式,对k和ε采用高阶Quick离散格式,对雷诺应力项采用一阶迎风格式是模拟旋风分离器气相流场的最佳选择.

图7 非稳态下的速度矢量分布Fig.7 Distribution of the velocity vectors in unsteacly state
[1]HSIEH K T,RAJAMANI R K.Mathematical model of the hydrocyclone based on physics of fluid flow[J].AIChE Journal,1991,37(5):735-746.
[2]闫顺林,杨玉环.新型高性能弯扭动叶旋转煤粉分离器特性 研 究[J].动 力 工 程 学 报,2012,32(2):140-145. YAN Shunlin,YANG Yuhuan.Characteristic study on high-performance rotary type pulverized coal classifier with bowed-twisted moving blades[J].Journal of Chinese Society of Power Engineering,2012,32(2):140-145.
[3]杨成禹.大型CFB 锅炉旋风分离器冷模试验研究[D].重庆:重庆大学动力工程学院,2006.
[4]MALHOTRA A,BRANION R M R,HAUPTMANN E G.Modeling the flow in a hydrocyclone[J].The Canadian Journal of Chemical Engineering,1994,28(3):953-960.
[5]宗涛,胡丹梅,李佳.基于CFD 的循环流化床旋风分离器数值模拟[J].上海电力学院学报,2011,27(3):242-246. ZONG Tao,HU Danmei,LI Jia.Numerical simulation of cyclonic separator in circulating fluidized bed boiler with CFD[J].Journal of Shanghai University of Electric Power,2011,27(3):242-246.
[6]WANG B,XU D L,CHU K W,etal.Numerical study of gas-solid flow in a cyclone separator[J].Applied Mathematical Modeling,2006,30(9):1326-1342.
[7]ELSAYED K,LACOR C.Modeling analysis and optimization of air cyclones using artifical neural network[J].Powder Technology,2011,212(4):115-133.
[8]CHU K W,WANG B,XU D L,etal.CFD-DEM simulation of the gas-solid of flow in a cyclone separator[J].Chemical Engineering Science,2011,66(11):834-847.
[9]NARASIMHA M,BRENNAN M S,HOLTHAM P N.Numerical simulation of magnetite segregation in a dense medium cyclone[J].Minerals Engineering,2006,19(3):1034-1047.
[10]QIAN Fuping,WU Yanpeng.Effects of inlet section angle on separation performance[J].Chemical Engineering Research and Design,2009,87(5):1567-1572.
[11]AZADI M,AZADI M,MOHEBBI A H.A CFD study of effect of cyclone size on its performance parameters[J].Journal of Hazardous Materials,2010,182(6):835-841.
[12]ELSAYED K,LACOR C.The effect of cyclone inlet dimensions on the flow pattern and performance[J].Applied Mathematical Modeling,2011,35(11):1952-1968.
[13]胡砾元,时铭显,周力行,等.旋风分离器三维强旋湍流流动的数值模拟[J].清华大学学报:自然科学版,2004,44(11):1501-1508. HU Leyuan,SHI Mingxian,ZHOU Lixing,etal.Numerical simulation of 3-D strongly swirling turbulent flow in a cyclone separator[J].Journal of Tsinghua University:Science and Technology,2004,44(11):1501-1508.
[14]刘淑艳,张雅,王保国.用RSM 模拟旋风分离器内的三维湍流流场[J].北京理工大学学报,2005,25(5):377-383. LIU Shuyan,ZHANG Ya,WANG Baoguo.Cyclone separator three-dimensional turbulent flow-field simulation using the reynolds stress model[J].Journal of Beijing Institute of Technology,2005,25(5):377-383.
[15]张海红.分离器流场与分离性能的数值模拟研究[D].河南:郑州大学化工过程与机械学院,2004.
[16]薛晓虎,孙国刚,时铭显.分离器内颗粒浓度分布特性的数值分析[J].机械工程学报,2007,43(12):26-33. XUE Xiaohu,SUN Guogang,SHI Mingxian.Numerical simulation on particle concentration distribution in cyclone separator[J].Chinese Journal of Mechanical Engineering,2007,43(12):26-33.
[17]何宏舟,黄俊斌.入口下倾旋风分离器分离特性的数值模拟[J].燃烧科学与技术,2010,16(6):532-535. HE Hongzhou,HUANG Junbin.Numerical simulations of gas-solid flow in a ramped entrance cyclone separator[J].Journal of Combustion Science and Technology,2010,16(6):532-535.
[18]薛晓虎,魏耀东,孙国刚,等.旋风分离器上部空间各种二次涡的数值模拟[J].工程热物理学报,2005,26(2):243-245. XUE Xiaohu,WEI Yaodong,SUN Guogang,etal.Numerical simulation on the secondary eddies in the upper space of a cyclone separation[J].Journal of Engineering Thermophysics,2005,26(2):243-245.
[19]SHUKLA S K,SHUKLA P,GHOSH P.Evaluation of numerical schemes using different simulation methods for the cyclone[J].Advanced Powder Technology,2011,22(11):209-219.
[20]FRASER S M,ABDEL R M ,ABDULLAH M Z.Computational and experiment investigations in a cyclone dust separator[J].Proc Instn Mech Engrs,1997,22(7):247-257.

