汽轮机重要易损部件中止样本集寿命数据管理系统的研究

杨 宇，史进渊，默静飞

（1.上海发电设备成套设计研究院，上海200240；2.中广核工程有限公司，深圳518031）

电站汽轮机的叶片、轴瓦、汽封、螺栓和阀杆等部件在运行中由于疲劳、磨损以及蠕变等导致损坏，通常在电站汽轮机检修中予以更换.这些被更换的部件称为汽轮机的易损部件.汽封等易损部件损坏不会造成严重后果，但会造成蒸汽泄漏量增加，进而导致汽轮机热耗率增加或振动增大.但是，叶片和轴瓦等易损部件损坏后则会导致电站汽轮机出力降低或强迫停机等严重后果，因此称为重要易损部件.

在电站汽轮机运行中经常出现部分部件失效而被更换时，部分未失效部件也同时被更换的情况.这种未失效但被中止的寿命数据和已失效部件的寿命数据合在一起构成的样本集称为中止样本集.大多数汽轮机易损部件在失效之前就按照制造厂要求在计划检修中已经予以更换，因此大多数汽轮机易损部件都属于中止样本集.

文献［1］介绍了全样本和定时截尾样本的电站设备易损部件寿命评定技术，然而到目前为止，有关中止样本集寿命数据预测方法的报道尚较少.因此，笔者认为研究电站汽轮机重要易损部件中止样本集的寿命预测模型，开发中止样本集寿命数据管理系统，从而使汽轮机重要易损部件的寿命周期处于受控状态，这对于电站汽轮机的长周期安全运行是一项十分有益的工作.

1 易损部件的寿命预测模型

1.1 威布尔模型

根据常年积累的电站汽轮机重要易损部件的设备台帐、运行数据以及检修记录能够获得汽轮机易损部件的累计运行小时数，并以此作为汽轮机易损部件的寿命数据.鉴于易损部件的寿命是随机变量，所以在可靠性工程中可以使用概率分布来描述这些随机变量的分布特性.文献［1］的研究得出，电站汽轮机易损部件的寿命数据通常服从威布尔分布.威布尔分布模型是可靠性领域里使用最广泛的模型，特别适合于疲劳、磨损、腐蚀、蠕变以及松弛等老化失效模式，而将正态分布和指数分布都近似看成是威布尔分布的特例.

当电站汽轮机易损部件的寿命数据服从三参数威布尔分布时，其失效概率分布函数F（t）和失效概率密度函数f（t）分别为：

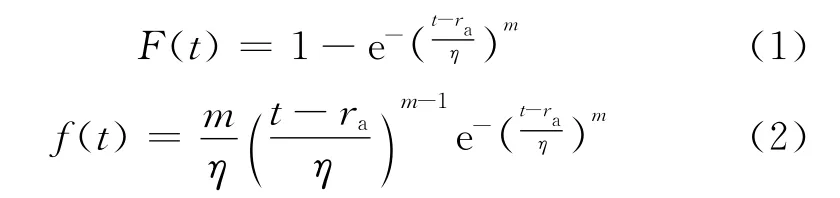
式中：ra为位置参数，ra≥0；η为尺度参数；m为形状参数.

当ra＝0时，汽轮机易损部件的寿命预测三参数威布尔模型退化为二参数威布尔模型.

1.2 易损部件寿命数据的分类

通过调研收集整理的电站汽轮机重要易损部件的现场累计运行时间、更换日期以及更换数量等组成的寿命数据样本集通常可分为三类：（1）所有部件均失效的寿命数据构成的完全寿命试验的全样本集；（2）部分部件失效，部分部件未失效但超过已失效寿命数据的寿命数据合在一起构成的定时截尾寿命试验的定时截尾样本集；（3）部分部件失效，部分部件未失效但被中止的寿命数据合在一起构成的中止样本集.中止样本集与定时截尾样本集的区别在于：前者样本集中部分虽未失效，但已被中止的样本的寿命数据小于已失效的最大寿命数据.

1.3 中止样本集的寿命数据分析

对于全样本集或定时截尾样本集，可以采用统计分析法来确定参数η和m，并可通过分布检验来判别寿命数据是否符合威布尔分布.根据文献［2］可知：当样本总数n大于25时，可采用最佳线性无偏估计方法进行参数估计；当样本总数n不大于25时，可使用简单线性无偏估计方法进行参数估计.

全样本集和定时截尾样本集易损部件寿命的统计分析方法详见文献［1］～文献［3］，本文不再赘述.笔者主要介绍现场最常见的电站汽轮机重要易损部件中止样本集寿命数据的统计分析方法.

对于中止样本集，由于其平均次序数不是整数，因此无法采用统计分析方法，通常采用线性回归分析方法来确定参数η和m［4］.

对三参数威布尔分布的分布函数式（1）变形后取双对数可得：

作如下变换：

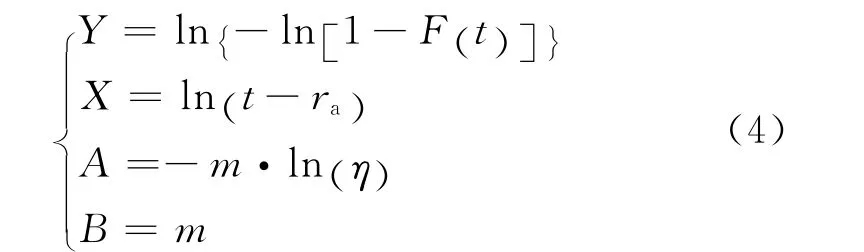
则式（3）可变为：

根据文献［4］，不同时间区段的各个故障概率分布函数可采用中位秩公式计算：

式中：F（ti）为ti区段的中止寿命数据的失效概率；n为样本集的样本总数；Ji为不同时间区段的平均次序数.

不同时间区段的平均次序数的计算公式为：

式中：Ji-1为不同时间区段的本次失效之前的失效样本数和中止样本数的平均次序数；ki为不同时间区段的失效样本数；Qi为不同时间区段的新增量.

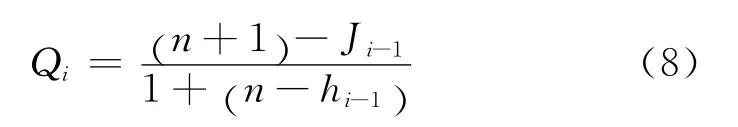
式中：hi-1为不同时间区段的本次失效之前的失效样本数和中止样本数之和.

根据样本数据（ti，F（ti）），通过式（4）得到新的数据（Xi，Yi），于是由线性回归分析得到参数η和m分别为：

检验统计量FC为：

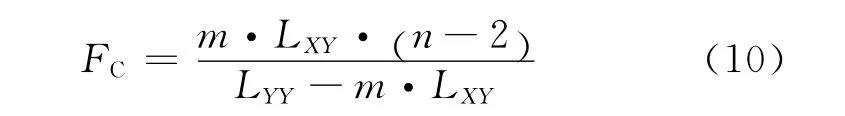
其中

如果FC＞Fα（1 ，n-2） ，则符合威布尔分布；反之，则不符合威布尔分布，需要调整位置参数ra的数值，重新计算有关参数.Fα1，n（ ）-2 为给定显著性水平α的F分布值.

2 易损部件的寿命预测方法

在电站汽轮机易损部件威布尔分布模型中的分布参数确定之后，就可以计算易损部件的可靠度、可靠寿命、更换周期、平均寿命以及检测周期等寿命指标，并能够为制定电站汽轮机易损部件的检测周期、检修计划和更换计划提供技术依据.

2.1 可靠度和可靠寿命

易损部件在规定条件下和规定时间t内完成规定功能的概率称为易损部件的可靠度，其计算式为：

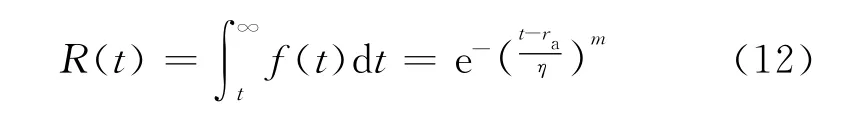
给定值可靠度R0所对应的时间tR0称为易损部件的可靠寿命，其计算式为：

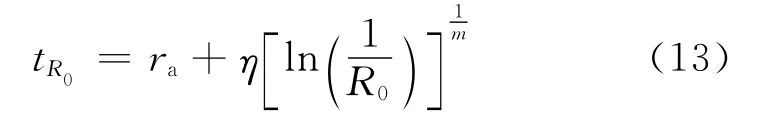
2.2 更换周期

易损部件被更换的时间间隔称为易损部件的更换周期.对于可靠度有一定要求的电站汽轮机易损部件，当其累积工作时间达到可靠寿命tR0时就应将其更换，否则就不能保证其安全可靠.根据易损部件失效后果的严重程度，确定更换周期tR0对应的可靠度要求以及相对应的可靠寿命作为易损部件的更换周期.易损部件可靠度的取值范围见表1.

表1 易损部件可靠度的取值范围Tabl.1 Reliability range of wearing parts

2.3 平均寿命

平均寿命就是寿命的平均值ti，f，其计算式为：

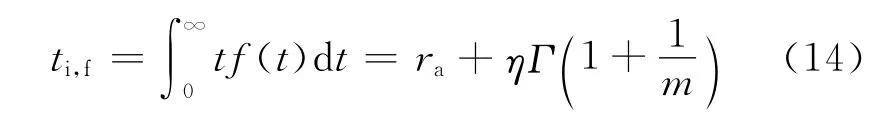
式中：Γ（s）＝∫∞0xs-1e-xdx（s＞0），称为参变量s的Γ函数.

2.4 检测周期

对于电站汽轮机的重要易损部件，可通过采用在线和离线高精度检测仪表或探伤设备定期检测其异常状态.监测易损部件的时间间隔称为易损部件的检测周期tm.制定合理的检测周期时，既要避免“多”检也要防止“漏”检，通常可根据易损部件的寿命预测模型结合更换周期动态制定检测周期.

根据文献［5］，在同类易损部件发生损坏的情况下，易损部件的检测周期为：

3 应用实例

某型号汽轮机某级有114 个333 mm 自由叶片，且8台运行汽轮机中有6台发生了叶片损坏事故.损坏叶片的运行小时数从小到大分别为4 865 h、8 494h、12 112h、17 107h、21 553h 和26 598 h，损坏叶片数分别为5个、6个、5个、5个、3个和6个.对发生事故汽轮机的处理措施为：更换已损坏叶片，把没有损坏的叶片锯断到323mm，并对其进行调频.对2台未发生叶片损坏事故的汽轮机，则不进行任何处理.

该样本集属于中止样本，样本总数n为912（114×8）个.根据式（10）计算出检验统计量FC为102 530.24，取显著性水平α＝0.1，Fα＝0.1（1，910）＝0.015 8.因为FC＞F0.1（1，910），所以该级叶片的寿命数据服从威布尔分布.根据式（9）和式（10）计算得到ra＝0，m＝1.370 7，η＝196 455.55h.根据式（14）计算得到平均寿命ti，f＝179 671.98h.汽轮机叶片失效会造成发电机组强迫停运.由表1可知，汽轮机叶片失效后果属于第Ⅳ类严重失效后果，其可靠度取为0.95，根据式（13）计算得到其更换周期取可靠寿命t0.95＝22 500.91h，如果每年运行7 000 h，当间隔达到3.2年时需更换该级叶片.根据式（15），汽轮机叶片的检测周期为tm＝8 983h.如果每年运行7 000h，则当间隔1.2年时需要揭缸对叶片进行检查.

如果电站无法实现每间隔3.2年更换该级叶片，则应在中间安排2次揭缸探伤等检测措施来对该级叶片状态进行识别.在进行揭缸探伤时，应做好检修预案，提前准备好备品备件，同时应加强汽轮机热力参数和振动特性的监测和趋势分析.当在线监测到热力参数和振动特性出现异常时，则有可能发生断叶片事故，应当立即停机，并对其进行开缸检查处理.

4 易损部件的寿命数据管理系统

为了使电站维护和管理人员在电站汽轮机易损部件寿命管理中更好地应用以上模型和方法，笔者在综合中止样本集、定时截尾样本集和全样本集寿命数据分析模型和寿命预测方法的基础上开发了电站汽轮机易损部件寿命管理系统.该系统主要包括寿命建模和寿命管理两部分.

寿命建模部分主要具有以下功能：（1）根据运行记录和检修记录收集整理电站汽轮机易损部件的历史数据，并计算出运行小时数等寿命数据；（2）根据样本集的特点确定样本集类型是全样本、定时截尾样本还是中止样本；（3）完成分布拟合检验并确定易损部件寿命数据的分布类型；（4）根据寿命数据的分布参数估计和确定易损部件的寿命预测模型；（5）计算易损部件的可靠度、可靠寿命以及平均寿命等寿命评定指标；（6）根据易损部件失效后果的类型确定易损部件更换的周期和检测周期.

寿命管理部分主要具有以下功能：（1）易损部件登记入库管理；（2）根据建立的寿命预测模型并结合易损部件当前运行数据绘制出寿命损耗指标图和趋势图，从而确定易损部件的监测日期和更换日期；（3）制定对应的监测、维修和更换计划；（4）将已完成的监测和维修结果输入数据库，更新运行数据，完成新一轮工作循环.

5 结 论

（1）电站汽轮机大部分易损部件的寿命数据样本集为中止样本集.本文给出的汽轮机中止样本集的寿命预测模型和寿命预测方法具有实际工程实用价值.

（2）采用电站汽轮机易损部件中止样本集的寿命预测方法和寿命数据管理系统可以优化汽轮机备件采购和管理，能够确定汽轮机易损部件监测、维修和更换计划，为汽轮机优化检修提供依据，并可使汽轮机易损部件的使用周期处于受控状态.

［1］史进渊，邹军，沈海华，等.电站设备易损件寿命评定与寿命管理技术的研究［J］.动力工程，2008，28（2）：225-228. SHI Jinyuan，ZHOU Jun，SHEN Haihua，etal.Study on life assessment and life management technology of easily damaged power equipment components［J］.Journal of Power Engineering，2008，28（2）：225-228.

［2］WILLIAM R.WESSEL S.Practical reliability engineering and analysis for system design and life-cycle sustainment［M］.Boca Raton，USA：CRC Press，2009.

［3］茆诗松，王铃铃.可靠性统计［M］.上海：华东师范大学出版社，1984.

［4］KAPUR K C，LAMBERSON L R.Reliability in engineering design ［M］.New York，USA：Joha Wiley and Sons，1977.

［5］苏坚，史进渊，杨宇，等.可靠性分析技术在电站主机和辅机状态检修中的应用［J］.动力工程，2003，23（6）：2833-2835. SHU Jian，SHI Jinyuan，YANG Yu，etal.Application of reliability analysis technology to maintenance based on condition for main equipments and auxiliaries in power stations［J］.Journal of Power Engineering，2003，23（6）：2833-2835.