涡旋式膨胀机的非线性数学模型及动态仿真

侯国莲，胡国强，毕珊珊，张建华

（华北电力大学 控制与计算机工程学院，北京102206）

膨胀机是有机朗肯循环系统（简称ORC 系统）中一个重要的部分，它利用从蒸发器出来的高温高压气体工质输出机械能并且带动发电机发电，实现了由机械能到电能的转化，工作原理如图1所示. 目前，用于ORC 系统的膨胀机主要分为两类：一类是速度型膨胀机，它利用喷嘴和叶轮将高温高压工质气体转化为高速流体，然后再将高速流体的动能转化为旋转机械能.速度型膨胀机功率越小，转速越高，甚至可能达到每分钟十几万转，因而速度型膨胀机不可能做得很小［1］.当前国内外关于ORC系统的研究大都属于小型或微型系统［2-4］，膨胀机不可能做得很大，因此速度型膨胀机只适用于小型或微型的有机朗肯循环系统.另外一类是容积式膨胀机，通过改变体积来获得膨胀比和焓降，适合于小流量、大膨胀比的场合，同时其输出功率较小，转速较低，并且输出功率随着转速的增大而增大，适用于小型或微型的ORC系统［1］.

图1 有机朗肯循环系统工作原理图Fig.1 Working principle of an organic Rankine cycle system

涡旋式膨胀机是容积式膨胀机的一种，由于其造价低、转速小和膨胀比大，在ORC 系统的研究中越来越受到人们的关注，关于涡旋式膨胀机的研究也越来越多.高小军等［5］研究了用于回收PEM 燃料电池能量的涡旋式膨胀机的性能，并且进行了该膨胀机的数字仿真.Vincent等［6-7］用涡旋式膨胀机的半经验模型预测了膨胀机在ORC 系统中的性能.Sylvain等［8］从膨胀机热力学性能的角度出发，根据膨胀机进气腔、膨胀腔、排气腔等组建的静态数学关系，提出了用于ORC 系统的涡旋式膨胀机静态数学模型，将根据模型计算得到的数据与膨胀机原型测得的数据进行对比，验证了此模型的有效性.之前关于涡旋式膨胀机模型的绝大多数研究都是从研究涡旋式膨胀机的热力学性能角度出发，基于模型参数间的变量静态关系建立数学模型，模型过于复杂.针对涡旋式膨胀机的控制设计，笔者选取R123为工质，从膨胀机系统的热力学机理分析出发，将机前阀门开度sz作为输入量，膨胀机转子转速N（或转子角速度w）作为输出量，利用数学建模的解析方法和步骤［9-10］，得出了涡旋式膨胀机的非线性微分方程，并进行了动态仿真.

1 涡旋式膨胀机的数学建模

涡旋式膨胀机的工作过程包括进气、膨胀、排气三个过程，这些过程可以分解为以下六部分［7］（1）suc-suc＿1：绝热压降；（2）suc＿1-suc＿2：等压降温；（3）suc＿2-adp：绝热可逆；（4）adp-exh＿2：绝热等容；（5）exh＿2-exh＿1：绝热混合；（6）exh＿1-exh：等压升温，如图2所示.

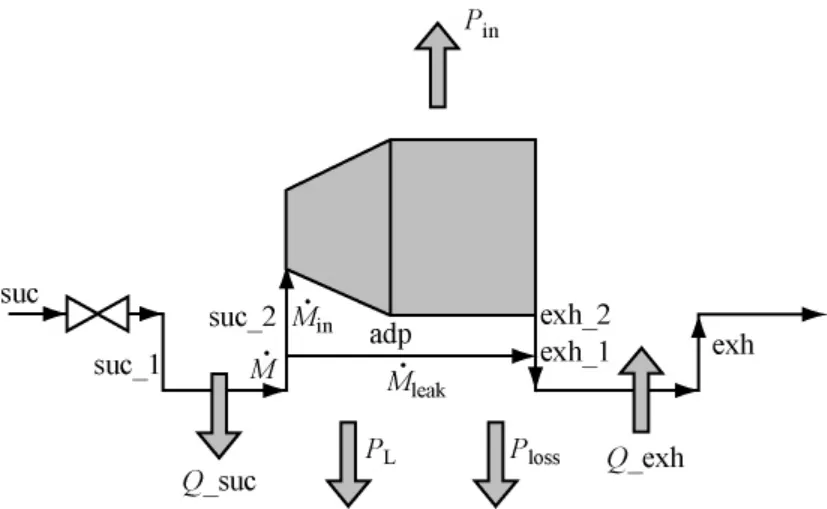
图2 涡旋式膨胀机工作过程的分解示意图Fig.2 Working process decomposition of a scroll expander

图2中suc表示涡旋式膨胀机进气口处；suc＿1表示膨胀机进气管道与进气腔连接处；suc＿2 表示膨胀机进气结束时动静涡盘所形成腔体内选取的平均点；adp表示膨胀机膨胀过程结束而排气还未开始时形成腔体内选取的平均点；exh＿2表示膨胀机从排气开始到排气结束时排气腔内的平均点；exh＿1表示与排气腔相连接的管道入口处；exh表示与排气腔相连接的管道出口处；Qsuc表示吸气过程所放出的热量；Qexh表示排气过程所吸收的热量；M·表示进入膨胀机的工质质量流量，kg／s；M·in表示进入膨胀腔内的工质质量流量，kg／s；M·leak表示工质进入膨胀机内泄漏的质量流量，kg／s；Pin表示进入膨胀机膨胀腔内的高压工质气体对外做功所产生的功率，W；PL表示负载消耗功率，W；Ploss表示由于摩擦等造成的机械损失功率，W.

1.1 系统建模假设

在建模之前先进行如下假设［6］：

（1）将suc-suc＿1 过程等效为等熵流通过一个收缩喷嘴的过程，收缩喷嘴的出口截面积（A2）近似为一个常数；

（2）进入膨胀机的工质的流速很小；

（3）气体工质为理想气体；

（4）工质气体常数（Rg）及绝热指数（κ）近似等于常数；

（5）进气管道及进气腔内的工质气体均匀分布，即在进气管道及进气腔内工质气体密度处处相等；并且认为气体流经该进气管道及进气腔时，其状态变化是按多变过程进行的.

1.2 涡旋式膨胀机变量静态关系

涡旋式膨胀机的静态关系是进气管道、进气腔、膨胀腔及排气腔等特性的综合，分析膨胀机动态特性是以静态关系为基础的.根据假设条件，得出以下主要静态关系［11-12］.

根据假设有：

式中：A2为收缩喷嘴出口截面面积，m2；cf2为收缩喷嘴出口截面上的速度，m／s；v2为收缩喷嘴出口截面上气体的比体积，m3／kg.

结合质量守恒方程和能量守恒方程，进入膨胀腔内的质量流量可以用下式表示.

式中：Asuc为进气口横截面积；hsuc和h分别为等效喷嘴进口和出口截面的比焓；vsuc＿1为等效喷嘴出口截面的比体积.

式中：csuc和csuc＿1分别为喷嘴进口和出口截面上的气流速度；h0为滞止时气体的焓.

式中：κ为等熵指数；psuc和psuc＿1分别为等效喷嘴进口和出口处的压力.

根据假设（2）可得

根据假设（3）可得

联立式（1）～式（8）可得

在文献［6］给定的工况下，按照式（9）计算进入膨胀腔内的质量流量为0.082 5kg／s，而实验测得的数据约为0.086 8kg／s，两者相差0.004 3kg／s，误差为4.95%，满足误差要求.

由式（9）可知，进入膨胀腔内工质质量流量的函数＝fM（psuc，Tsuc）可用抛物线函数或线性函数近似［13］，本文用psuc和Tsuc的线性函数组合近似：

1.3 非线性微分方程及求解

根据能量守恒和质量守恒原理，建立涡旋式膨胀机系统的非线性微分方程.

（1）根据进气管道及进气腔输入与输出的总质量守恒，推导容积方程，这一方程描述了阀门开度与进气管道及进气腔中工质压力的关系.图3为进气管道及进气腔容积的示意图.

图3中为流过节流阀的工质质量流量，取决于阀门开度sz，即

为进入膨胀腔的工质质量流量，取决于进气腔进气管道入口处的压力psuc和温度Tsuc，而psuc和Tsuc取决于容积内积存工质的多少.

图3 进气管道及进气腔容积的示意图Fig.3 Pressure-volume diagram of the inlet pipe and inlet chamber

根据假设（4）和（5）有

式中：Vs，exp为膨胀机排气体积，属于膨胀机的结构参数，为常数.

将式（10）、式（11）和式（13）代入式（12）可得

因为ρsuc、psuc和Tsuc均是可变的，所以式（14）是一个非线性微分方程.

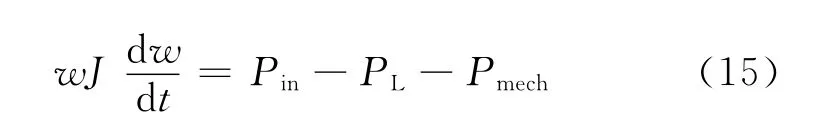
式中：Pin为工质气体进入膨胀机内做功产生的功率.

式中：τp为压力比，τp＝为膨胀机的等熵效率，是压力比τp和转速N的函数，由于工作中其值变化范围不大，这里取常数［6］；PL表示负载消耗功率，是一个取决于外部因素的量；Pmech是由于摩擦等造成的机械损失功率，是一个与w有关的非线性函数，可近似认为［6］

式中：Tloss为机械损失转矩，可认为是常数.

将式（10）、式（16）和式（17）代入式（15）后得

由于w、psuc、Tsuc均是可变的，因此式（18）是一个非线性微分方程.利用小偏差线性化的方法将其转化为一个近似线性方程.设ρ0、psuc，0、sz0均为额定工况下所对应的参数，则每个变量都可以写成额定值加变化量的形式，即

将式（19）代入式（14），得

故式（20）可简化为

与ρsuc，0、psuc，0和Tsuc，0相比，Δρsuc、Δpsuc和ΔTsuc仅仅是个很小的变化量，所以通过小偏差线性化可将近似为这种近似结果影响甚微.实践表明，这种简化所带来的误差仅为1%～2%［14］.

同理，对式（18）进行小偏差线性化，将式中所有变量记为常量与小偏差的和，即

由Pin，0-PL，0-Pmech，0＝0

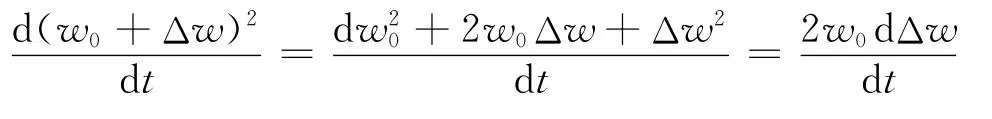
2 模型理论验证及动态仿真

本文中涡旋式膨胀机的工作点为：转速N0为2 296r／min，即ω＝240.436 6rad／s；膨胀机入口压力psuc，0和入口温度Tsuc，0分别为1.003 MPa和415K，膨胀机出口压力pexp，0为0.201 MPa，工质为R245fa.此工况条件下的计算结果如下：τp＝0.200 4，κ＝1.15，τκ＝0.130 4，ηexp＝66.25%，ρsuc＝52.206 9 kg／m3.此 时κ1＝0.234 5，κ2＝-0.000 104 75，κ3＝-0.104 9.

在阀门开度和负荷发生扰动时进行仿真实验.

（1）当给阀门开度sz一个幅值为1 的阶跃变化、仿真时间取0.1s时，仿真曲线如图4所示.

图4 进气管道入口压力随阀门开度扰动的动态响应Fig.4 Dynamic response of inlet pressure with disturbance of valve opening

由图4可知，当阀门开度阶跃变化时，膨胀机进气管道入口压力能够在极短的时间内达到稳定，这是因为与汽轮机相比，涡旋式膨胀机本身的功率极小，而汽轮机的容积时间常数通常为0.1～0.3 s［14］，所以膨胀机的进气管道及进气腔的容积效应对进气的影响极小，其动态响应时间极快，这与实际情况相符.

（2）当给膨胀机内部功率Pin一个幅值为0.01的阶跃变化时，膨胀机角速度相对变化量的变化曲线如图5所示.

图5 膨胀机角速度随内部功率扰动的动态响应Fig.5 Dynamic response of angular velocity with disturbance of internal power

由图5可知，在时间为6s左右时，曲线达到了稳定，说明随着膨胀机内部功率的变化，膨胀机的转速能够在很短的时间内趋于一个稳定值，这与实际中膨胀机小功率的特性相吻合.

（3）当阀门开度不变，负荷阶跃扰动为0.005、0.01和0.015时，动态响应曲线分别如图6（a）、图6（b）和图6（c）所示.

由图6可知，在相同阀门开度下，当负荷扰动逐渐增大时，膨胀机转速变化量的稳定值减小.

（4）当负荷不变，阀门开度阶跃扰动分别为0.02和0.03时，涡旋式膨胀机角速度相对变化量的响应曲线如图7（a）和图7（b）所示.

图6 负荷阶跃扰动时涡旋式膨胀机角速度相对变化量的响应曲线Fig.6 Dynamic response of angular velocity with load disturbance

图7 阀门开度阶跃扰动时涡旋式膨胀机角速度相对变化量的响应曲线Fig.7 Dynamic response of angular velocity with disturbance of valve opening

由图7可知，当阀门开度增大时，膨胀机转速的稳定值也逐渐增大，这是因为阀门开度增大时，膨胀机进气管道及进气腔内储存的工质质量流量增大，从而使进入膨胀机膨胀腔内做功的工质流量增大，膨胀机发出的功率增大，在负荷一定的情况下带动膨胀机转子的转速增加.

3 结 论

（1）两组非线性微分方程的动态仿真结果与涡旋式膨胀机功率小、动态响应快等特点相符.

（2）在相同阀门开度扰动时，在不同负荷扰动情况下，转子转速的变化量与负荷变化的趋势一致；在相同的负荷扰动下，随着阀门开度增大，转子转速也相应地增加.仿真结果表明所建立的模型从机理上正确地反映了涡旋式膨胀机的特点.

［1］顾伟.低品位热能有机物朗肯动力循环机理研究和实验验证［D］.上海：上海交通大学机械与动力工程学院，2009.

［2］刘广彬，赵远扬，李连生，等.低温余热回收用涡旋膨胀机性能模拟研究［J］.西安交通大学学报，2009，43（7）：88-91.LIU Guangshan，ZHAO Yuanyang，LI Liansheng，et al.Simulation of scroll expander used in low-temperature waste heat recovery system［J］.Journal of Xi＇an Jiaotong University，2009，43（7）：88-91.

［3］王辉涛，王华.低温太阳能热力发电有机朗肯循环工质的选择［J］.动力工程，2009，29（3）：287-291.WANG Huitao，WANG Hua.Selection of working fluids for low-temperature solar thermal power generation organic Rankine cycles［J］.Journal of Power Engineering，2009，29（3）：287-291.

［4］LEMORT V，QUOILIN S，PIRE C.Experimental investigation on a hermetic scroll expander［C］／／7th International IIR Conference Compressors.Papiernicka：Compressor，2009.

［5］GAO X J，LI L S，ZHAO Y Y，etal.Research on a scroll expander used recovering work in a fuel cell［J］.International Journal of Thermodynamics，2004，7（1）：1-8.

［6］LEMORT V，QUOILIN S，CUEVAS C，etal.Testing and modeling a scroll expander integrated into an organic Rankine cycle［J］.Applied Thermal Engineering，2009，29（14／15）：3094-3102.

［7］LEMORT V，QUOILIN S，LEBRUN J.Numerical simulation of a scroll expander for use in a Rankine cycle［C］／／Proceeding of the International Compressor Engineering Conference at Purdue.Purdue：［s.n.］，2008.

［8］QUOILIN S，LEMORT V，LEBRUN J.Experimen-tal study and modeling of an oraganic Rankine cycle using scroll expander［J］.Applied Energy，2010，87（4）：1260-1268.

［9］谢兆鸿，范正森，王艮远.数学建模技术［M］.北京：中国水利水电出版社，2003.

［10］陈理荣.数学建模导论［M］.北京：北京邮电大学出版社，1999.

［11］沈维道，蒋智敏，童钧根.工程热力学［M］.北京：高等教育出版社，2006.

［12］QUDILIN S.Experimental study and modeling of a low temperature Rankine cycle for small scale cogeneration［D］.Liège：Faculty of Applied Sciences Aerospace and Mechanical Engineering Department，University of Liège，2007.

［13］AILER P，SANTA I，SZEDERKENYI G.Nonlinear model-building of a low-power gas turbine［J］.Periodica Polytechnica Ser Transportation Engineering，2001，29（1／2）：117-135.

［14］郭钰峰，徐志强，于达仁.汽轮机调节原理［M］.北京：机械工业出版社，2010.