充流管道单向流固耦合数值模拟自动化研究
陈坚红,周天情,盛德仁,李 蔚,陈 辉
(1.浙江大学 热工与动力系统研究所,杭州310027;2.山东电力工程咨询院有限公司,济南250013)
充流管道系统在电力、石油、化工等各类工业装置中有着广泛的应用,充流管道的流固耦合(FSI)振动是当前理论和工程研究的热点[1-4].流体在管道中流动会对管道产生一定的作用力,使管道产生一定的变形,而管道的变形会促使流体的流场发生改变,变化后的流场又给管道结构带来新的激励,这种相互作用的过程就是流固耦合过程[5].近几十年来,国内外学者对流固耦合的理论和计算方法开展了广泛的研究,取得了一些成果.但是,由于流固耦合问题存在复杂性,流固耦合方程的建立还存在许多假设,远远不能达到解决实际工程问题的需要,因此有必要进行深入研究.对于流固耦合过程的求解,比较简单的问题可以采用解析法和半解析法,而具有复杂边界条件的实际工程问题则很难给出解析解,需要采用数值计算方法进行反复迭代计算才能得到分析结果[6].由于采用数值计算方法计算一个完整的流固耦合过程时,计算量比较大,且实际工程中大多数充流管道的计算只需考虑流体对管道结构的作用——单向流固耦合过程,因此,单向流固耦合过程的求解对充流管道的计算有重要的现实意义.
许多学者利用数值模拟方法对单向流固耦合过程进行了求解,并取得了一定成效.偶国富[7]运用Ansys有限元分析软件,采用物理环境顺序偶合法进行单向流固耦合;杨振国等[8-9]采用Ansys结构分析软件与流体分析软件CFX 进行单向流固耦合的模拟;杨涛等[10-13]将Fluent流场分析软件与Ansys结构分析软件相结合,用线性插值、曲线拟合以及取近似值等方法实现了流场数据与结构数据的传递.然而,以上研究均为对某个具体问题而进行的单向流固耦合数值模拟,模拟时要逐步进行软件操作和数据处理,过程极为复杂,而且在流体计算与结构计算之间的数据传递上也采取了近似算法,计算的准确性有待检验.为了解决以上单向流固耦合数值模拟中操作过程复杂、数据传递失真的问题,笔者采用C++语言编写充流管道流固耦合数值模拟程序,对Gambit软件、Fluent软件和Ansys软件进行封装,实现对一个三维充流管道进行单向流固耦合数值模拟的自动化计算分析,程序的计算流程为:先在Gambit软件中对管道和流体进行建模,并划分好网格,然后导入到Fluent软件中进行流体数值模拟,将经过流体计算后的管道网格模型连同其所受载荷一起导出,程序对导出的数据进行相应整理,并用APDL 参数化语言编制出Ansys软件的命令流文件.最后程序调用Ansys软件使其自动读取APDL命令流文件,无失真地加载经过流体计算后的管道网格模型连同其所受载荷,并进行结构分析.
1 数值计算方法及程序实现
1.1 单向流固耦合的数值计算方法
管道中流体的流动满足质量守恒定律、动量守恒定律和能量守恒定律,这些规律体现在流体力学中就是相应的连续性方程和流体运动方程(即N-S方程)[14].
按照质量守恒定律,对于某一控制体内的流体,其连续性方程的积分形式为
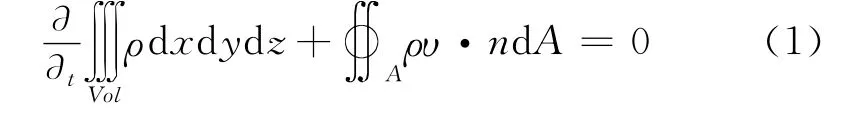
式中:Vol表示控制体;A表示控制面.根据奥-高公式,在直角坐标系中,对于不可压缩的均质流体,可将上式化为以下微分形式:
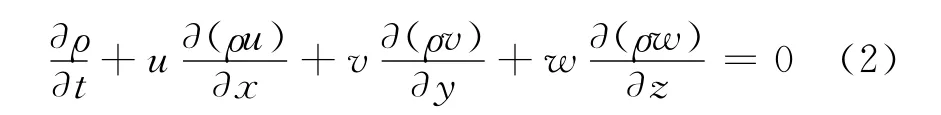
对于密度和黏性系数为常数的流体,其运动方程(N-S方程)为以下矢量形式:
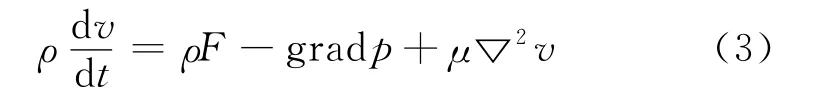
N-S方程比较准确地描述了实际的流动.黏性流体的流动分析可归结为对此方程的研究.
管道结构可以简化为线性振动系统.对于一个自由度为n的线性管道振动系统,假设系统中各质量、刚度和阻尼已知,根据牛顿第二定律以及Mykles-tad法,该系统的运动微分方程为
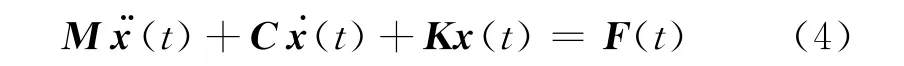
式中:M、C、K分别为n阶对称正定质量矩阵、n阶阻尼对称方阵和n阶刚度对称方阵;F(t)为管道所受外力.
求解弹性机翼气动力的基本思想有弱耦合法(loose coupling method)和强耦合法(tight coupling method)[15].同样,求解充流管道的流固完耦合方法也分为弱耦合法和强耦合法.
弱耦合法即传统的耦合流体分析模式和结构分析模式的方法,首先完成流体分析,收敛的流体分析结果转移到结构分析中,用有限元方法计算结构变形之后,针对变形的结构再进行流体分析,重复此过程直至结构变形收敛;强耦合方法中,流体方程和结构方程是同时求解的,即在流体方程求解迭代期间,间断地按照还未收敛的流体来计算结构变形,再把变形量代入流体计算的迭代过程中,直到结构变形和流体力都收敛.
对于弱耦合法,只须将每次流体计算收敛后的流体力F(t)代入式(4)中即可进行结构分析,即完成了一步单向弱流固耦合计算.
对于强流固耦合,流体运动在结构上产生的作用力须转换为以下形式:

式中:Ma、Ca、Ka分别为流体作用对结构产生的附加n阶对称正定质量矩阵、附加n阶阻尼对称方阵和附加n阶刚度对称方阵,其均为流动状态的函数,随流体流动状态的变化而变化[5].
将式(5)代入式(4)中,得

每进行一次式(6)的计算就完成了一步强流固耦合计算.
由于一方面强耦合算法计算量太大,且目前还处于基本理论的研究阶段;另一方面弱耦合算法能充分利用现有计算流体力学和计算结构力学的方法和程序,只要增加数据交换模块即可[16].因此,目前大多数耦合计算都建立在弱流固耦合的基础之上.
本计算程序利用Fluent软件和Ansys软件来进行充流管道单向弱流固耦合的计算.对于内部充满流体的管道,管内流体的流动状态可以根据式(1)和式(3)由Fluent软件进行模拟计算,然后将流体计算结果加载到管道内壁上,进而根据式(4)由Ansys软件进行管道结构分析.
1.2 程序实现方法
Gambit软件和Fluent软件在操作过程中会生成相对应的操作命令流文件,这些操作命令流文件能直接被软件读取,只要将事先编制好的操作命令流文件导入到软件中,便可实现软件的自动化运行.而Ansys软件提供了一种运行批处理命令的APDL 格式,只要事先编制好APDL 代码并导入到Ansys中运行,即可实现Ansys软件的自动化分析.基于上述思路,用C++语言编制出一种用户界面和计算过程控制程序,该程序具有以下功能:(1)管道模型参数和流体状态参数通过程序界面上的对话框输入;(2)程序根据输入的各类参数自动生成相应的Gambit操作命令流文件、Fluent操作命令流文件及Ansys的APDL 命令流文件;(3)程序能自动将Fluent软件的计算结果导出,并无失真地转换成Ansys结构分析所需的各类文件,供Ansys软件调用;(4)程序能先后自动控制调用Gambit软件、Fluent软件和Ansys软件并执行对应的命令流文件;(5)计算完成后,程序能清晰地显示出所需的流体分析结果和结构分析结果.程序的运行流程如图1所示.
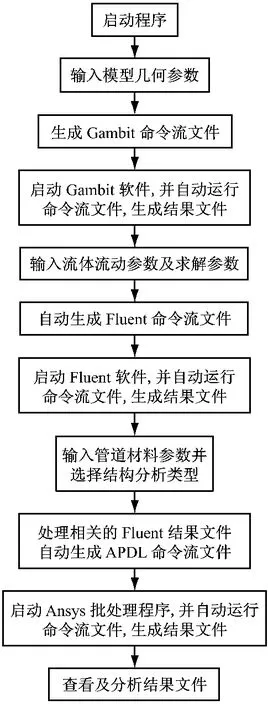
图1 程序运行流程图Fig.1 Flow chart of the program
2 充流管道数值模拟分析
2.1 程序计算结果验证
为了验证该程序计算方法的可行性与计算结果的准确性,对与参考文献[17]中相类似的充流管道模型进行数值计算,并将计算结果与试验结果进行对比分析.
文献[17]中作为对比的全钢充流直管段长为3.81m,内径为0.08m,管壁厚度为0.004 5m,钢的杨氏弹性模量为21.06×1010Pa,泊松比为0.3,管道内液体密度为1 000kg/m3,流速为8.5 m/s.文献中所进行的测试为模态测试.按照图1所示的流程,进行相关参数的输入,选择结构分析类型为“模态分析”.在Fluent软件中进行流体计算后可得到管道内壁受到的压力值,将该值导入到Ansys软件中可得图2所示的压力云图.
通过Ansys软件中的模态分析,可得到该段充流管道的各模态频率,对文献[17]中图6的频响曲线进行统计,也可得出各阶频率值.将本程序的计算结果与文献[17]中的试验结果进行对比,可得到各阶频率所对应的误差率,如表1所示.

图2 全钢充流直管的压力云图(单位:Pa)Fig.2 Pressure distribution of the fluid-filled steel pipeline(unit:Pa)
由表1的数据可以看出,本程序计算出的各阶频率值与文献[17]中模态测试所得的各阶频率值非常接近.因此,可以认为采用该计算程序对充流管道进行单向流固耦合数值模拟是可行的,且计算结果是准确的.
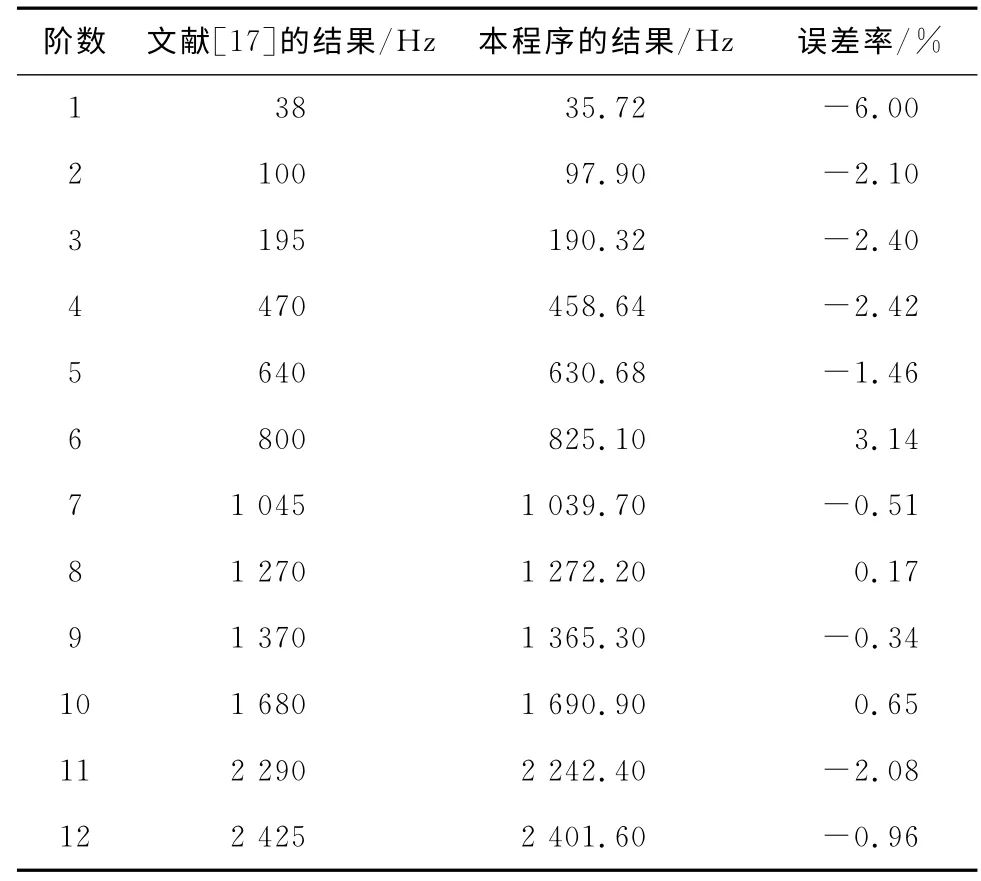
表1 充流管道模态频率Tab.1 Modal frequency of the fluid-filled pipeline
2.2 充流管道的应力分析
在工程管道设计中,常用的管道应力分析软件如CAESAR II、GLIF等并不能准确地将管道内部流体的压力分布施加到管道内壁上,从而导致计算出的管道应力结果不够准确.该计算程序能够耦合流体计算和结构计算,准确获知管道内壁的压力分布,使得管道的计算应力值更加准确.
以某火力发电厂1 000MW 超超临界机组6号低压加热器的疏水管道中两个支吊架之间的一段为例进行计算.该管段由半径相等、两两相互垂直的三段直管通过两段90°弯头相连接而成,其内径为0.257m,壁厚为0.008 m,管道内壁粗糙度为0.046mm,三段直管的长度依次为1.8 m、3.7 m和2.0m,两端弯管的弯曲半径均为0.381m.
根据以上结构尺寸,在程序中输入相应的参数,程序自动调用Gambit软件进行模型建立、网格划分及边界的定义,结构及网格划分如图3所示.

图3 疏水管道模型图Fig.3 Modelling of the drain pipeline
通过程序自动启动Fluent软件,并在相应的数据输入对话框中输入疏水流动参数:入口压力为0.229 MPa、入口温度为124.6 ℃、入口的流速为1.273m/s.然后Fluent软件自动进行流体分析,并将计算结果自动保存.图4为管道壁面所受的压力云图.
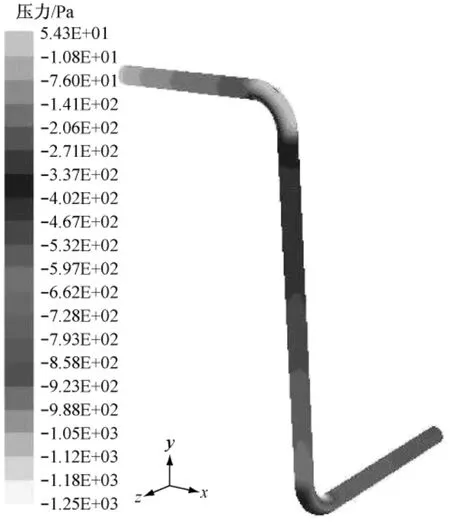
图4 疏水管道内部流体压力云图Fig.4 Fluid pressure distribution in the drain pipeline
Fluent计算完成后,操作程序对Fluent软件导出的计算结果进行自动处理,以便无失真地导入到Ansys软件中.然后操作程序自动启动调用Ansys软件、读入处理过的结果文件并自动进行静力分析.在静力分析过程中,施加在管段上的力包括重力和流体压力,管段受到的约束包括起始端的刚性固定和末尾段的X方向限位约束.
经过上述流体分析和结构分析可得,该管段所受到的最小应力为0.148 MPa,最大应力为24.8 MPa,应力云图如图5所示.
通过以上实例可知,该计算程序完全能够模拟充流管道内部流体压力分布,并根据流体压力进行管道应力计算,它可以用于异径管、周期管等特殊管道的应力计算,从而弥补了通用管道应力分析软件的不足.在阀门、大小头以及喷嘴等管件的设计改造中,该计算程序也可以用来进行流体流场模拟和结构应力计算,以获得更好的性能和使用寿命.另外,该计算程序还可用于对正在使用中的充液管道进行风险预测,找出管道中可能出现故障的位置,及时采取相应的安全措施.

图5 疏水管道应力图(单位:Pa)Fig.5 Stress distribution of the drain pipeline(unit:Pa)
2.3 程序的进一步发展
程序能够方便地实现从流体计算到结构分析的单向流固耦合数值模拟,在此基础上,只要稍加改进就可以完成完整的流固耦合过程的数值分析.具体的改进方法如下:获取结构计算后各节点的位移信息,对变形后的充流管道进行重新建模,然后在更新后的模型中再进行流体计算和结构分析,如此往复循环,直至最终的管道结构分析计算结果收敛.
3 结 论
采用C++语言编程技术对Gambit软件、Fluent软件和Ansys软件进行封装,编制出一个可对三维充流管道进行单向流固耦合数值模拟的程序,实现了从模型建立、流体计算到结构分析过程的自动化,确保了从流体计算到结构计算过程数据传递的准确性.通过与参考文献试验结果的对比,证明该计算程序对充流管道进行单向流固耦合数值模拟是可行的,且计算结果是准确的.实例计算表明,该程序在充流管道单向流固耦合数值模拟中具有操作简便、结果准确的特点,可应用于多种充流管道的设计改造和风险预测中.
[1]PITTARD M T,EVANS R P,MAYNES R D,et al.Experimental and numerical investigation of turbulent flow induced pipe vibration in fully developed flow[J].Review of Scientific Instruments,2004,75(7):2393-2401.
[2]TIJSSELINGA A S,VARDY A E.Fluid-structure interaction and transient cavitation tests in a T-piece pipe[J].Journal of Fluids and Structures,2005,20(6):753-762.
[3]YANG Ke,LI Qiusheng,ZHANG Lixiang.Longitudinal vibration analysis of multi-span liquid-filled pipelines with rigid constraints[J].Journal of Sound and Vibration,2004,273(1/2):125-147.
[4]LI Qiusheng,YANG Ke,ZHANG Lixiang,etal.Frequency domain analysis of fluid-structure interaction in liquid-filled pipe systems by transfer matrix method[J].International Journal of Mechanical Sciences,2002,44:2067-2087.
[5]张立翔,杨柯.流体结构与互动理论及其应用[M].北京:科学出版社,2004:37-42.
[6]朱洪来,白象忠.流固耦合问题的描述方法及分类简化准则[J].工程力学,2007,24(10):92-99.ZHU Honglai,BAI Xiangzhong.Description method and simplified classification rule for fluid-solid interaction problems[J].Engineering Mechanics,2007,24(10):92-99.
[7]偶国富,许根富,朱祖超,等.弯管冲蚀失效流固耦合机理及数值模拟[J].机械工程学报,2009,45(11):119-124.OU Guofu,XU Genfu,ZHU Zuchao,etal.Fluidstructure interaction mechanism and numerical simulation of elbow erosion failure[J].Chinese Journal of Mechanical Engineering,2009,45(11):119-124.
[8]王宇飞,杨振国.气-液两相流对管道性能影响的有限元模拟分析[C]//第14届全国反应堆结构力学会议论文集.桂林:中国力学学会,中国核学会.2006:99-101.
[9]刘志远,郑源,张文佳,等.Ansys-CFX 单向流固耦合分析的方法[J].水利水电工程设计,2009,28(2):29-31.LIU Zhiyuan,ZHENG Yuan,ZHANG Wenjia,et al.The method of single-track fluid-structure interaction analysis by Ansys-CFX [J].Design of Water Resources &Hydroelectric Engineering,2009,28(2):29-31.
[10]杨涛.液力缓速器流场仿真及有限元分析[D].武汉:武汉理工大学汽车工程学院,2009:32-37.
[11]曾强.压气机转子叶片流固耦合计算及软件集成研究[D].南京:南京航空航天大学能源与动力学院,2006:20-25.
[12]王鄢.大型离心压缩机叶轮动力分析方法研究[D].大连:大连理工大学工程力学系,2009:30-33.
[13]马廷卫.混流式水轮机转轮结构分析研究[D].四川:西华大学能源与环境学院,2006:20-22.
[14]韩占忠,王敬,兰小平.Fluent流体工程仿真计算[M].北京:北京理工大学出版社,2008.
[15]KIM Y,KIM J,JEON Y,etal.Multidisciplinary aerodynamic-structural design optimization of supersonic fighter wing using response surface methodolo-gy[C]//40th AIAA Aerospace Sciences Meeting.Reno:NV,AIAA,2002.
[16]安效民,徐敏,陈士橹.二阶时间精度的CFD/CSD 耦合算法研究[J].空气动力学学报,2009,27(5):547-552.AN Xiaomin,XU Min,CHEN Shilu.Analysis for second order time accurate CFD/CSD coupled algorithms[J].Acta Aerodynamica Sinica,2009,27(5):547-552.
[17]WEN Jihong,SHEN Huijie,YU Dianlong,etal.Theoretical and experimental investigation of flexural wave propagating in a periodic pipe with fluid-filled loading[J].Chin Phys Lett,2010,27(11):133-136.

