一种码长变化灵活的重复累加码构造方法

刘焕兵，陈 翔，姜 晖

(合肥电子工程学院，安徽 合肥 230037)

低密度奇偶校验(LDPC)码[1]已成为当今信道编码领域的研究热点之一，其随机化编码思想和概率迭代译码算法使其具有逼近香农限的性能，与Turbo码一起成为当今性能最优越的纠错码，具有较高的研究价值。LDPC码和Turbo码都能达到逼近香农限的性能，Turbo码能实现线性编码复杂度，但译码复杂度比较高;LDPC码能实现线性译码复杂度，但编码复杂度较高。而IRA码不仅是一类“Turbo－like”码—串行级联卷积码，而且是LDPC码的一个子类，集合了两者的优点，既能实现线性编码复杂度，又能实现线性译码复杂度，Hui Jin等人提出的IRA码具有简单的原模图和优越的次数分布对。本文在其基础上，结合准循环码的方法，对每个子矩阵进行具体设计，构造出码长灵活可变、性能优越的LDPC好码。

1 原理

1.1 低密度奇偶校验码

LDPC码是一种(n，k)线性分组码，码长为n，信息序列长度为k，可以由校验矩阵H唯一定义[2]。H的维数是m×n，每一行对应一个校验方程，每一列对应码字的一列。每一行和每一列中非零元素的个数为行重、列重。式(1)是一个5×10的校验方程，其中码字c=(c1，c2，c3，c4，c5，c6，c7，c8，c9，c10)∈C，满足 H·c=0，即

除了用校验矩阵表示LDPC码以外，还可以用双向的模型图表示，其中Tanner图表示是比较方便的一种，可以形象地描述LDPC码的编译码特性。图1是与式(1)对应的 LDPC码的 Tanner图，包含变量节点(VN){bj，j=1，2，…，n}、校验节点(CN){ci，i=1，2，…，m}和连接它们的边，其中VN对应校验矩阵H的列，即码字的每个码元，CN对应H的行，即每个校验方程，第j个VN和第i个CN有连接的边就意味着H的i行j列元素不为零。与第j个VN相连的边的个数称为该变量节点的度或次数(degree)，等于H第j列的列重与第i个CN相连的边的个数称为该校验节点的度或次数，等于H第i行的行重。

图1 LDPC码的Tanner图

LDPC码的环定义为Tanner图中由VN，CN和连接它们的边首尾相连组成的闭合环路，次数分布是指具有相同次数的节点所对应的与之相连的边占总边数的比例。短环和次数分布对是影响非规则LDPC码性能的两大主要因素，在LDPC码构造时，要尽量避免环尤其是短环的出现。

传统的LDPC编码主要采用高斯消去法编码。用给定的M×N的校验矩阵H，编码后得到的码字c应满足HcT=0。LDPC码的高斯消去法产生如图2所示的下三角矩阵。若将c分成两部分，即s代表信息序列，p代表校验序列，则系统编码可分为两个步骤:第一步将长度为N－M的信息序列直接给s赋值，第二步通过后向递推得到p，其中第i个校验比特pi为

高斯消去法编码复杂，需要进行的运算量为N2。

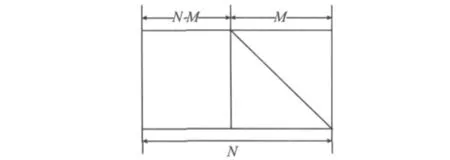
图2 高斯消去法

1.2 非规则重复累加码

Hui Jin等人提出IRA码是一种简单的类Turbo码，同时也是一种特殊的LDPC码，这种码编码简单，仅由重复器、交织器和累加器组成，译码可由高速并行的置信传播(BP)译码器实现，从而实现了线性的编译码复杂度。

IRA码是由一个重复器和一个累加器，中间级联一个交织器组成，其编码原理如图3所示。长度为K的信息序列进入重复q次，然后经过一个交织器，随机交织，最后经过累加器进行累加，最后输出校验序列P。

图3 IRA码编码原理

IRA码可以由原模图表示，即节点数量较少的Tanner图，如图4所示，通过原模图进行“复制—置换”操作，可以得到任意大小的Tanner图。原模图用G=(V，C，E)表示，其中V，C和E分别是其变量节点、校验节点和边的集合。

图4 非规则重复累加码的原模图

1.3 准循环构造方法

一些线性分组码(n，k)的码字循环移位n0(n=zn0，k=zk0)次后得到的仍是该码的一个码字，这类码称为准循环(QC)码[3－4]。准循环码的校验矩阵完全由其前k0行决定，编码也可用移位寄存器实现，降低了编码器的复杂度。其循环右移过程如图5所示。

图5 准循环码的循环右移过程

2 设计方案

首先通过文献[5]中给出的原模图得到次数分布对和未具体设计子矩阵的基校验矩阵，然后通过准循环的方法对子矩阵进行具体设计，最后对校验矩阵进行去四环优化。

2.1 IRA码

非规则重复累加码的原模图由图4给出，可以看出原模图包含6个变量节点，3个校验节点、边数，将其转换到校验矩阵形式，得到校验矩阵的列重分别为 3，4，3，2，2，2，行重分别为5，6，5。可以由其设计校验矩阵Hm×n(m=3，n=6)，表示为

式中:Π1代表列重为1的子矩阵，Π2代表列重为2的子矩阵，0代表全零阵。IRA码的次数分布对为

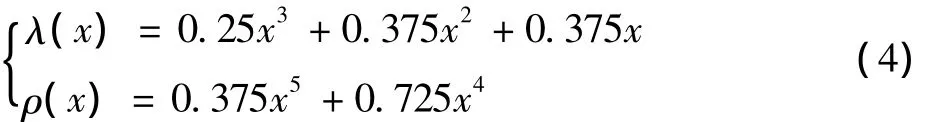
2.2 子矩阵设计

对于列重为1的子矩阵，利用单位矩阵进行循环右移，对于列重为2的子矩阵，利用双对角线阵进行循环右移，如图6所示，全零阵保持不变。

定义基准矩阵Bm×n(m=3，n=6)为子矩阵循环右移次数的集合，其表达式如式(5)所示。基准矩阵Bm×n对应检验矩阵 Hm×n，如果 b1，1=12，则代表 Hm×n中第一行第一列个子矩阵循环右移次数为12

图6 双对角线阵循环右移过程

单位阵、双对角线阵、全零阵都是z×z方阵，z的大小可灵活选取，从而构造码长不同的LDPC码。

2.3 去四环优化

LDPC码的环[6]是指Tanner图中由变量节点、校验节点和连接它们的边首尾相连组成的闭合环路。环长是指其中包含的变数，环长最小值为4。四环是影响LDPC码性能的重要因素，因为Tanner图中的环特别是长度较短的循环使译码不充分，使节点之间传递的外部信息的独立性减小，减低了抗干扰能力，从而使译码算法无法收敛到一个最优的译码效果，造成了性能的下降。

为了进一步提高码的性能，对校验矩阵进行去四环优化。本文构建校验矩阵使用的子矩阵是单位阵和双对角线结构的准循环矩阵，结合单位阵、双对角线阵、准循环的特殊性，所以只要满足以下两个条件，校验矩阵中就不会出现四环:

1)对于由单位矩阵得到的循环右移子矩阵，应满足

式中:1≤i＜i+m≤3，1≤j＜j+n≤6。

2)对于由双对角线矩阵得到的循环右移子矩阵，应满足

式中:1≤i＜i+m≤3，1≤j＜j+n≤6。

在产生B基准矩阵后，经过验证，如果不满足以上条件，则重新生成，直至产生不存在四环的B基准矩阵，本文使用的基准矩阵如式(8)所示，经验证，满足以上条件

3 仿真结果及分析

在加性高斯白噪声信道(AWGN)中，采用二进制相移键控(BPSK)调制，置信传播译码算法迭代50次，验证算法构造LDPC码的的性能。

仿真1:比较码长变化时码的性能。将子矩阵大小z取值25，50，100，200，从而构造码长为 150，300，600，1200的码，对其进行性能比较，其结果如图7所示，可以看出，当码长变化时，码的性能始终保持在一个较好的范围之内，虽然码长变化，但次数分布对并没有改变，四环也没有增加。随码长增加，码字性能逐渐变好。

图7 码长变化灵活的非规则重复累加码的误比特率性能

仿真2:比较去四环之前与去四环之后码的性能。z取值100，码长为600，仿真结果如图8所示，可以看出优化去四环之后，码的性能有了明显的改善，去四环之前，LDPC码的误差平层较高，在高信噪比区域曲线下降的趋势变缓，从而证明了四环是影响LDPC码重要因素之一。

图8 去四环之前与去四环之后的码性能仿真图

仿真3:比较算法构造的LDPC码与IEEE 802.16e标准规定的LDPC码性能。z取值100，码长为600，IEEE 802.16e标准规定的LDPC码码长为576，其仿真结果如图9所示。

图9比较了算法构造码与IEEE 802.16e标准规定的LDPC码性能，可以看出，本文构造的LDPC码与标准中规定的LDPC码性能极为接近，当误块率为0.01时，差距在0.5 dB以内，说明所构造的LDPC码也达到了逼近香农限的性能。

图9 算法构造的LDPC码与IEEE 802.16e标准规定的LDPC码性能比较

4 小结

本文在一类IRA码优越的次数分布对基础上，利用准循环码原理具体设计了基校验矩阵，并进行了去四环优化。通过仿真结果和理论分析可以得到，利用算法构建优化的LDPC码，码长变化灵活，性能比优化前有明显提高，十分接近IEEE 802.16e标准规定的LDPC码性能，在电视信号传输领域具有较好的应用前景。

[1]GALLAGER R G.Low－density parity－check codes[EB/OL].[2011－08－09].http://www.rle.mit.edu/rgallager/documents/ldpc.pdf.

[2]袁东风，张海刚.LDPC码理论与应用[M].北京:人民邮电出版社，2008.

[3]FOSSORIER M P C.Quasicyclic low density parity check codes from circulant permutation matrices[J].IEEE Trans.Information Theory，2004，50(8):1788－1793.

[4]刘春江，吴智勇，于新，等.一类准循环LDPC码的快速编码方法[J].电视技术，2007，31(6):11－13.

[5]JIN H，KHANDEKAR A，MCELIECE R.Irregular repeat－accumulate codes[EB/OL].[2011－08－09].http://www.ee.caltech.edu/EE/Faculty/rjm/papers/Brest00.pdf.

[6]陈翔.LDPC码链路自适应技术研究[D].北京:北京理工大学，2009.

[7]龚昊，龙沪强，张罗鸣，等.一种低误码平层的LDPC码的构造与实现[J]. 电视技术，2008，32(S1):106－109.