一种具有最小距离下界的正则LDPC码的构造

王 娟，王中训，朱方强，刘 丽

(烟台大学，光电信息科学技术学院，山东 烟台 264005)

低密度校验码(LDPC码)是一种逼近香农限的好码[1]。PEG 算法是构造中短长 LDPC 码的最优方法[2]，该算法可以得到较大的围长和较大的最小距离下界[3]。本文提出一种通过不断改善独立树基础的最小距离下界的构造LDPC码的新方法。与用PEG方法构造的LDPC码相比，独立树基础LDPC码改进了围长和最小距离下界，得到了更低的误码率性能。

1 背景介绍

1.1 LDPC码的表示

LDPC码可以由其稀疏校验矩阵H唯一定义。矩阵中的行对应校验方程，列对应码字的比特。LDPC码还可以用变量节点(矩阵中的列)校验节点(矩阵中的行)组成的Tanner图来表示[4]，当校验矩阵元素非零时，Tanner图中的变量节点和校验节点之间有一条边相连。在Tanner图最短的循环长度称为LDPC的围长[5]。

1.2 经典PEG方法和改进的PEG方法

PEG方法是不断往开始只有校验节点的Tanner图中添加特点度数的变量节点去构造具有大围长的LDPC码。每往Tanner图中添加1条边，添加的边的环长是目前可获得的最大环长。此过程直到添加的比特节点的数目达到要求的个数。

经典的PEG方法构造出来的LDPC码的矩阵不能满足校验节点度分布的约束[3]。校验节点的规则性对译码收敛速度和硬件实现都是有利的[6]。变量节点从合法的校验节点的集合中选取，每增加一条边都需要检验新增加边的校验节点的度是否达到了预设值dc，直到选取到达到预设值的校验节点。对PEG方法做这样小的改动能增加校验节点的规则性，却对LDPC码的围长性能几乎没有影响。

码的围长可用来求最小距离下界[3]。对规则LDPC码，当是奇数，则

在第2章将提出用独立树得到新的下界，这个界比式(1)，(2)中的围长为基础的下界都要紧。

1.3 独立树的构造

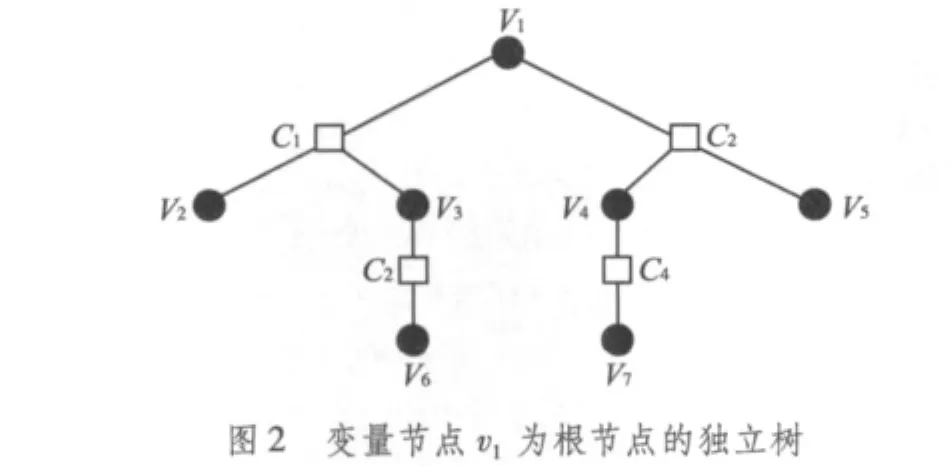
独立树是Tanner图的一个联通子图，为的是最大化根节点与叶节点之间的距离。独立树的每个变量节点都连接了Tanner图中它的一部分邻居节点。每个校验节点也和Tanner图中的同样的邻居节点相连。这种对变量节点的安排，既能满足Tanner图的校验节点的约束，也能满足独立树对每个校验节点的约束。

构造独立树的具体步骤是:以vi为根节点建造树，对每一级中的每个变量节点vk进行构造，即当校验节点cj∈A(vk)但不是vk的根节点时，则将cj连接到vk上，将除vk外属于A(vk)的变量节点即vl∈N(cj)vk置于下一级中;对每个变量节点vi都用这种方法去构造独立树。

图1给出N=7，K=3的LDPC码Tanner图，图2为构造的该LDPC码的变量节点v1为根节点的独立树，所有码字在Tanner图上的构造与独立树上的有效构造是一致的，而且独立树上关于最小重量的有效构造不能超过码字的最小距离。

2 独立树基础LDPC码的构造与其最小距离下界

由Tanner图的构造与独立树构造的关系，使得从独立树去改善码的性能成为可能。为了得到独立树根节点的最小距离下界，必须计算独立树上的最小距离偏差。通过独立树计算最小距离偏差的方式是去将所有变量节点的对数似然比赋值为1，然后从叶节点到根节点用最小和算法(MS)进行译码[7]。MS算法在根节点vi的结果就是独立树的最小重量偏差的重量，记作DITB，i。下面给出计算 DITB，i的方法。

定理1:LDPC码的最小距离下界满足

定理2:以独立树基础构造的LDPC码的下界都不小于以围长为基础构造的LDPC码的最小距离下界DGmin。

由定理1、定理2，很容易可以看出DITB，min也不小于式(1)，(2)中给出的界。以下给出了用独立树方法构造规则LDPC码的方法。

从含有N个变量节点，M个校验节点，校验节点度数为dC、变量节点为dV的任意规则LDPC码开始进行构造。

1)用以上介绍的构造独立树的方法以码的N个变量节点为根节点构造N个独立树。

2)所有成对的边，与它们相连的变量节点不与任何常规校验节点的相邻;初始化设 DITB－min=DITB，1，对任意的 i均有 DITB－min=DITB，i。

3)转换已经连接了校验节点的边ei和ej。

4)DITB－min减小时，或者 DITB－min没有减小，但是满足DITB－min=DITB，i的 i的数目减小，或者 DITB－min没有变，但是满足 DITB－min=DITB，i的 i的数目也没有变，相对所有的 i来说，DITB，i的平均值减小了，均保持步骤3)的转换。

5)否则取消这种转换。

必须说明，独立树LDPC码构造方法比PEG方法计算复杂度要高。PEG方法是在确立Tanner图上的最小环长之后添加一条边;而独立树LDPC构造用更精确的标准，从总体上估计每条可能的边的转换影响，这使得该算法需要进一步改进。

3 比较独立树和PEG法构造的LDPC码

从码的性能和仿真结果上将独立树构造的LDPC码分别与随机构造的、PEG构造的LDPC码进行比较。

表1将码长分别为N=1008，1512的3种方法构造的LDPC码的围长进行了比较。对N=504的码来说，独立树与PEG有同样的环长。N=1008和N=1512时独立树构造比其他两种方法围长要大，独立树构造方法在得到最大化最小距离下界的过程中得到了大的围长。

表1 几种LDPC码的构造方法性能比较

图3、图4是用BP算法在最大迭代次数为60次时的误码率仿真结果。

图3 N=1008时仿真结果

由以上仿真图可以看出当信噪比增加时，独立树构造码的误码率最低，并且会低于10－5。这是因为在信噪比增加时，围长和最小距离对性能有非常重要的影响。每种码长的码的仿真结果与表1给出的性能是一致的，最小距离下界越大误码率性能则越低。

4 结论

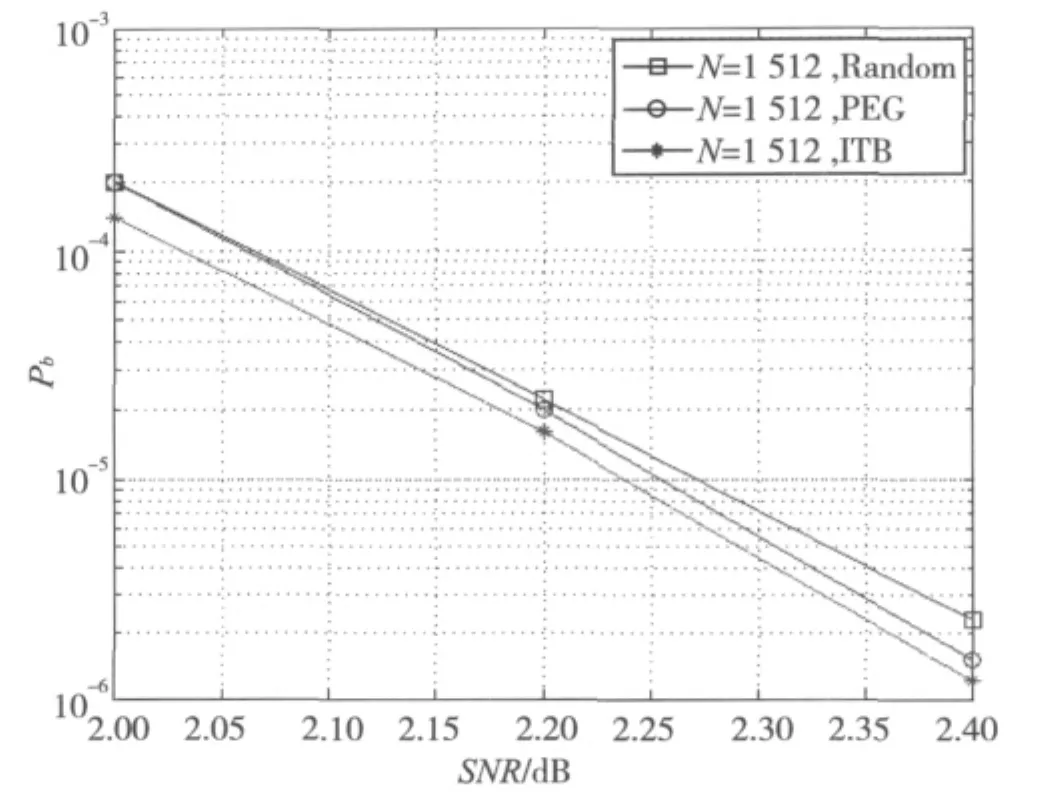
图4 N=1512时的仿真结果

本文给出一种新的独立树结构基础上的最小距离下界的构造规则LDPC码的方法，新方法的最小距离下界比以围长为基础的用PEG方法构造的规则LDPC码最小距离下界要大。而且这种方法构造的规则LDPC码得到了更长的围长、更大的最小距离下界以及更低的误码率性能。通过使用BP算法在AWGN信道下仿真的性能比较可知，随着信噪比的增加，该方法的误码率性能越明显优异于随机构造方法和PEG构造方法。

[1]MACKAY D J C，NEAL R M.Near shannon limit performance of lowdensity parity check codes[J].IEEE Elctron.Lett，1996，32(18):1645.

[2]雷伟龙，钱辰，王昭诚，等.基于PEG算法的QC－LDPC码构造[J].电视技术，2011，35(5):1－4.

[3]HU Xiaoyu，ELEFTHERIOU E，ARNOLD D M.Progressive edgegrowth tanner graphs[C]//Proc.Global Telecommunications Conference.San Antonio，TX，USA:IEEE Press，2001，2:995－1001.

[4]WIBERG N，LOELIGER H A，KOTTER R.Codes and iterative decoding on general graphs[J].Transctions Telecomm，1995，6(5):513－525.

[5]袁东风，张海刚.LDPC码理论与应用[M].北京:人民邮电出版社，2008.

[6]CHEN H，CAO Zhicang.A modified PEG algorithm for construction of LDPC codes with strictly concentrated check－node degree distributions[C]//Proc.IEEE Wireless Communications and Networking Conference(WCNC 2007).[S.l.]:IEEE Press，2007:564－568.

[7]李千玲，陈伟，樊丰.基于DVB－S2标准的LDPC码最小和译码算法的改进[J]. 电视技术，2011，33(5):8－9.