基于Hertz接触力模型的惯性平台内框架组件失稳倒台动力学建模与仿真分析

高 准，屈孝池，张天孝，杨朋军，弓 靖

(中国航天科技集团公司 第十六研究所，西安 710100)

惯性平台是集机、电、光为一体的复杂精密导航设备［1］。惯性平台失稳倒台是各种类型惯性平台的常见故障。当惯性平台稳定回路的某一环节发生故障时，会使惯性平台不能稳定在惯性空间，即平台失稳，引起倒台。失稳倒台发生后，会使平台失效，飞行任务失败。

本文基于Hertz接触力模型建立惯性内框架组件倒台时的数学动力学模型。之后使用Ansys Workbench仿真软件，计算出在倒台过程中挡块的应力分布云图。将Ansys Workbench仿真结果与所建立的数学模型相比较，证明了所建立的动力学模型以及各项分析的正确性［2］。

1 Hertz接触力模型

1.1 内框架运动学方程

图1 内框示架组件受力示意图Fig.1 Sketch map of the force about inner gimbal component

内框架组件与橡胶挡块的碰撞受力如图1所示:其中Fx(t)，Fy(t)为外框架施加给内框架转轴的力，F为内框架与橡胶挡块碰撞产生的力。假设一开始内框架为竖直，由所建立的模型可知内框架逆时针转过45°后与安装在外框架的橡胶挡块发生碰撞。该型号内框架组件绕其转轴的转动惯量Iz=2.55×105g·cm2，内框架组件失稳倒台时力矩电机施加的力矩为M=0.9 N·m，可以计算出内框架组件倒台后与橡胶挡块碰撞前一瞬间内框架的角速度为:

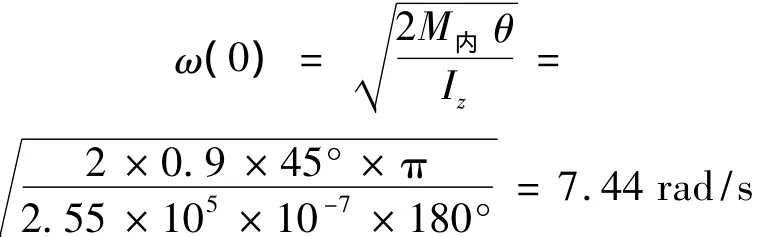
在对内框架倒台进行力学分析时，根据Hertz接触模型，可以假设内框架挡块的材料即橡胶挡块性质符合图2中的弹簧－阻尼器力学模型。其刚度系数和阻尼系数分别记为k和c［3，5］。记t=0为碰撞开始时刻。

图2 橡胶挡块等效为弹簧－阻尼器模型Fig.2 View rubber obstructive block as spring-damp model

碰撞时内框架组件逆时针转动，F1为弹力，F2为阻尼力，方向如图2所示。可得:F=F1+F2。在碰撞发生前一时刻，内框架的转速为ω(0)，在碰撞发生t时刻后设内框架的转速为ω(t)，简记为ω。所以在该瞬时，由Hertz弹性接触理论得到内框架所受的碰撞力F=k δ+c。其中 δ为橡胶挡块的变形量，为橡胶挡块的变形速度，则根据运动关系及所建立的模型有:

式中:0.035为内框架转轴与碰撞点的距离，如图1所示。

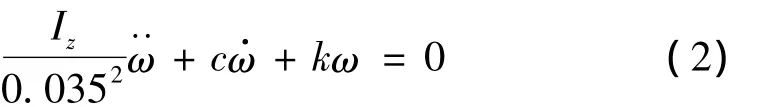
式中:常数k称为Hertz刚度系数，它与接触面的材料性质、接触面的曲率半径有关;c为阻尼系数，完整的表达式为c=c(δ)，是关于橡胶形变量δ的变量。为了分析内框架角速度的变化，需要分别讨论这两项系数。

1.2 刚度系数与阻尼系数

查阅相关手册［6］可得 Hertz刚度系数其中R，R为两碰撞物接触12处的曲率半径;为材料参数，定义为，式中μi为泊松比、Ei为弹性模量。最后根据该型号惯性平台的实际情况，将两碰撞物的材料代入刚度系数k的表达式，得内框架组件与挡块的接触刚度系数k=1.2425×107N/m。

阻尼系数c(δ)=λδ，其中λ称为滞后阻尼系数，em为碰撞恢复系数，则根据能量损失和经验公式［7］可得:

可以看到阻尼系数 c(δ)为随着形变δ改变的量。考虑到形变δ的值较小及后续求解的简便性，可以近似认为阻尼系数c(δ)不变，且为减少误差可令其中δm为压缩阶段弹簧－阻尼力学模型的最大压缩量。根据能量转化的关系，可以计算出δm=ω(0)·ω(0)，，k均为已知量，则可知。通过使用仿真工具Ansys Workbench的计算，得到的平均碰撞恢复系数是 em=0.57，最终可得阻尼系数 c(δ)=4071.6。

1.3 角速度与碰撞力

在内框架组件与橡胶挡块发生碰撞的前一瞬间，内框架组件的角速度ω(0)=7.44 rad/s;此时开始产生碰撞力，而且碰撞力是由弹簧－阻尼器力学模型中的阻尼器施加给内框架组件的，该阻尼力只与橡胶挡块的形变速度有关，即ω(0)Iz=－0.0352c ω(0)。以上两个条件作为式(2)的边界条件。而刚度系数k，阻尼系数c为常数，代入内框架组件转动惯量Iz的值，令，因此式(2)为二阶常系数奇数线性微分方程组。所以列写微分方程的特征方程，并且设r为特征方程的根得:

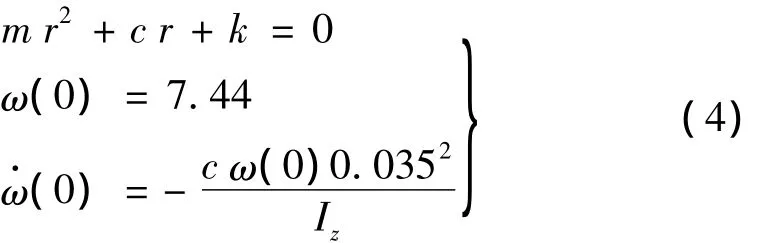
得内框架组件的角速度表达式为:

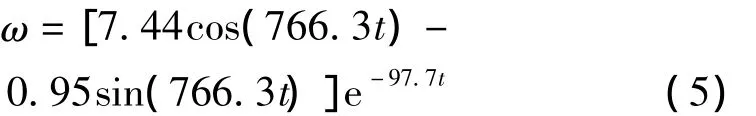
还可得在任意时刻的碰撞力为:

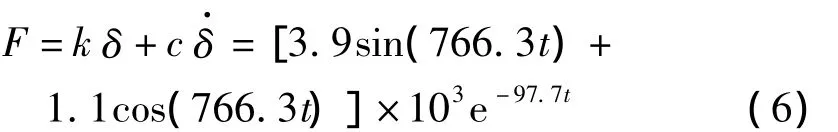
根据式(5)、式(6)计算出内框架的角速度、碰撞力变化情况，结果如图3所示:

可以看到，一开始碰撞力随着时间的延长而增大，这是因为在橡胶压缩阶段，橡胶的形变量越大，弹力越大，在0.001604 s时，橡胶的弹力达到最大值为3522 N。而过了碰撞力最大值后，碰撞力逐渐变小，这是因为橡胶的形变减小，使得碰撞力变小。大约在0.00376 s时，碰撞力最小，可以预见此时内框架组件与橡胶档钉不再接触。

图3 内框架组件碰撞力变化过程Fig.3 The change process of inner gimbal component force because of impact

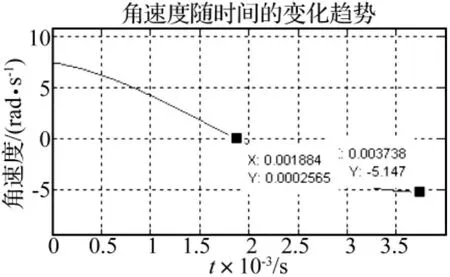
图4 内框架组件转速与时间段关系Fig.4 The change process of inner gimbal component rotate speed because of impact

图4为内框架组件的角速度变化曲线。在碰撞发生的一瞬间，内框架组件的角速度通过理论计算为:ω(0)=7.44 rad/s(在此规定角速度与力矩逆时针为正)。所以从图可知，一开始内框架组件逆时针转动，碰撞之后速度开始变小，直至变为零。在碰撞力的最大处，内框架组件的角速度最小。由于还存在碰撞力，且碰撞力产生的力矩为顺时针，所以内框架组件的角速度开始为负，并顺时针转动。外框架组件最终的转速为ω末=5.14 rad/s，这是因为没有发生完全弹性碰撞，在碰撞点有能量的损失，所以最终的角速度小于发生碰撞一瞬间时的角速度。角速度最小的时间是0.00373 s，碰撞力的最小时间是0.00376 s，误差为0.5%。

2 内框架结构建模及仿真

2.1 结构及其有限元简图

本文利用Pro/ENGINEER软件构造出惯性平台外框架与内框架组件的简化结构。通过软件的测量功能来得到简化的内框架组件的质量和绕内框架组件转轴的转动惯量，通过调节内框架组件的密度保证最终得到的简化与实物的转动惯量相同。图5为系统的内框架组件简图和有限元模型。

根据该型号惯性平台的实际情况，内框架组件的转动惯量为:Iz=2.55×105g·cm2，根据三维建模软件，令简化的内框架组件密度为 ρ=2.933×104kg/cm3。在Ansys Workbench里，输入三个零件的材料参数。根据实际倒台时的情况，施加约束条件和力矩，进行仿真计算。

图5 内框架组件结构简图及其有限元模型Fig.5 Structure and FEM of inner gimbal component

2.2 碰撞力仿真结果

设置好上述材料、载荷等参数之后进行计算，橡胶挡块的碰撞应力变化以及应力云图分布如图6所示。

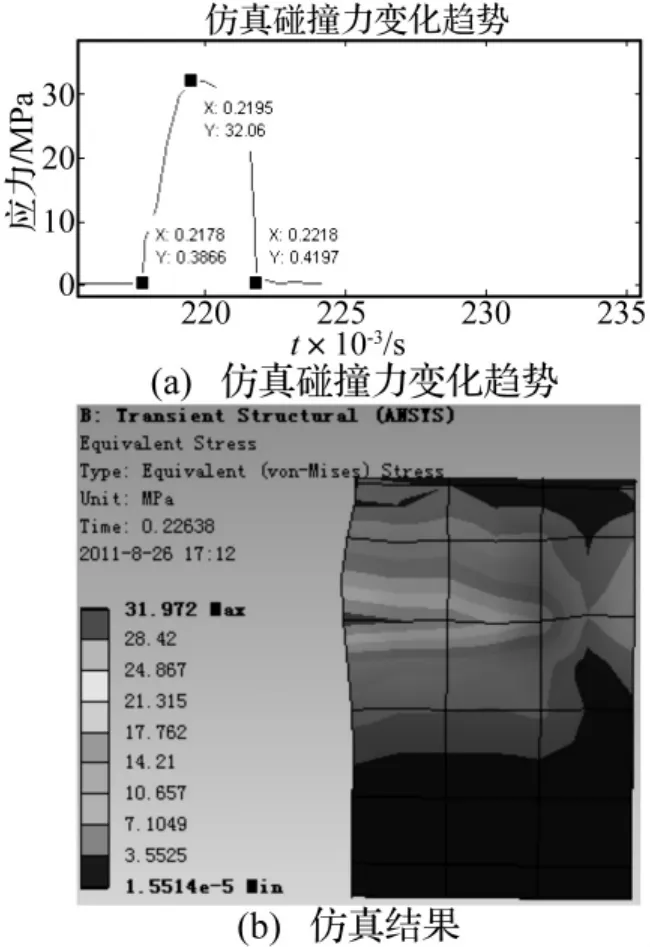
图6 有限元分析碰撞力的变化及云图分布Fig.6 The distributing of inner gimbal component force by FEM

从图中可以看出:在t=0.21784 s时，碰撞开始;在t=0.2195 s时，碰撞应力达到最大，为32.06 MPa;在t=0.2218 s时，碰撞结束。总的碰撞时间为:t=0.004。与所建立模型相比，时间误差为8%。满足工程中小于10%的要求。

由图还可以看出:碰撞面最大应力为32.06 MPa，根据仿真情况，划分单元格时的长度为5mm，所以根据图6(b)可估算出，碰撞面积约为100mm2，碰撞力为:

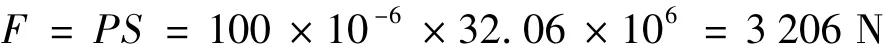
模型的碰撞力为3522 N，两者的误差为9%，符合工程中小于10%的要求。

3 结论

本文基于Hertz接触力模型，建立内框架组件倒台动力学模型，全面分析了内框架倒台时候的碰撞力和角速度变化过程。并通过仿真软件，输入倒台时内框架的各项物理参数、边界条件以及所受的外部载荷。通过仿真，证明了使用Hertz接触力模型是可以求取内框架倒台时候的碰撞力，并且误差满足工程要求，为后续的平台设计提供了重要的参考。

［1］钟万登.液浮惯性器件［M］.北京:宇航出版社，1994:220－222.

［2］杨朋军，王 卿，王佳民，等.惯性平台台体组件动态分析及台体结构优化设计［J］.战术导弹控制技术，2005，(1):54－58.YANG Peng-jun，WANG Qing，WANG Jia-min，et al.Inertial platform component dynamic analysis and platform structure optimal design［J］.Control Tecnology of Tactical Missile，2005(1):54－58.

［3］金东平，胡海岩.碰撞振动与控制［M］.北京:科学出版社，2005:29－40.

［4］孙德伟，张广玉.橡胶隔振器迟滞阻尼特性识别的新方法［J］.振动与冲击，2010，29(4):164 －168.SUN De-wei，ZHANG Guang-yu.A new approach to identify hysteretic damping of a rubber isolator［J］.Journal of Vibration and Shock，2010，29(4):164 －168.

［5］韩德宝，宋希庚.橡胶隔振器刚度和阻尼本构关系的实验研究［J］.振动与冲击，2009，28(1):156 －157.HAN De-bao，SONG Xi-geng. Experimentalstudy on constitutive model for damping and stiffness of a rubber isolator［J］.Journal of Vibration and Shock，2009，28(1):156 －157.

［6］徐 灏.机械设计手册［M］.北京:机械工业出版社，1991:275－285.

［7］和兴锁.理论力学－高等动力学［M］.西安:西北工业大学出版社，2001:7－9.