外环位移控制与内环力控制拟动力试验方法

谭晓晶，吴 斌

(哈尔滨工业大学 土木工程学院，哈尔滨 150090)

拟动力试验已经成为结构抗震试验的一个重要技术手段［1－4］。传统的拟动力试验多以位移控制为主，这是因为位移的求解及实现相对容易，同时还能很好地保护试验结构。但是，试验加载系统的位移控制分辨率是有限的，对于大刚度、小变形结构试验，加载系统的位移控制分辨率大于位移控制误差，那么拟动力试验将失效。相比较而言，试验加载系统的力控制分辨率却远小于大刚度结构试验的力控制误差，采用力控制的拟动力试验容易实现。现代的结构抗震试验越来越趋向于足尺、大型结构模型试验，因此研究力控制下的拟动力试验方法很有必需。

对于力控制下的拟动力试验研究，刘季等［5］把地震作用增量和结构惯性力增量之和作为试验加载的力命令作用于结构，同时测得结构的位移增量，并识别结构当前时间步的等效剪切刚度用以求解下一时间步的位移增量和力命令。李暄等［6］、王凤来等［7］根据实测的结构位移增量和反力增量来识别结构当前时间步的等效剪切刚度用以求解下一时间步的力命令。Pan等［8］采用了位移和力混合控制对隔震装置进行拟动力试验，在力控制阶段始终采用结构的初始刚度与预测位移的乘积作为试验力命令。Nakata等［9］提出了作动器的力和位移混合控制加载方法，该方法根据测量的结构反力和位移响应识别结构的刚度，再把力命令转换为位移命令，并通过内环的位移控制实现期望的力命令。Sivaselvan等［10］通过在刚性结构与作动器之间安装弹簧，从而把作动器的力控制转换为位移控制，解决了力控制加载时存在的自然速度反馈问题。Kim等［11］提出了力控制与位移控制之间的切换控制试验方法，在试验初期采用力控制，当结构软化时则采用位移控制。采用力控制时，通过识别结构的切线刚度或者通过Krylov子空间法把位移命令转换为力命令。可以看出，前述研究者在对于力控制加载试验方法问题上，大多数都是通过不断地识别试验结构的刚度，从而把位移命令转换为相应的力命令来加载，而通常结构的刚度识别比较复杂和困难。

为了实现大刚度结构的拟动力试验加载，同时也为了避免试验结构刚度识别的困难，本文提出了外环为位移控制内环为力控制的混合控制方法。通过在试验结构上安装高精度位移传感器采集结构的位移反应，使之与位移命令之间形成反馈控制，同时设置一个位移与力转换系数，把位移命令转换为力命令，作动器采用力控制加载。这样就形成了外环为位移控制、内环为力控制的混合控制加载模式。值得指出的是，外接的位移传感器不宜直接接入作动器的内部控制环，因为试验设备之间可能存在不匹配的情况。

1 试验原理

对于大刚度结构的界定，可以采用加载设备的刚度来进行，而加载设备的刚度可由其力量程与位移量程之比来定义。可以认为大于加载设备刚度的结构为大刚度结构，反之为小刚度结构。大刚度结构加载试验，结构的位移反应通常比较小，加载设备位移传感器的精度通常难以满足试验要求，那么可以采用外接高精度位移传感器来完成结构的位移测量。同理，当加载设备力传感器的精度不能满足试验要求时，可以采用外接高精度力传感器来完成结构的反力测量。

下面以中心差分法为例介绍力和位移混合控制拟动力试验方法的原理。试验结构的离散时间运动方程为:

速度和加速度假定分别为:

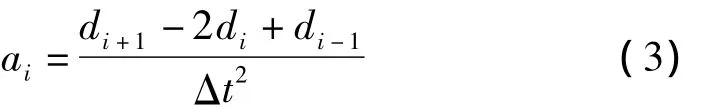
式中，M，C分别为质量矩阵和阻尼矩阵;R为恢复力向量;F为外荷载向量;d，v，a分别为位移向量、速度向量和加速度向量;Δt为积分时间步长;i为时间步数。

将(2)式和(3)式代入(1)式，整理得到:

从式(4)可以看出，di+1很容易根据测得前一时间步的R(di)计算得到，是需要实现的目标位移。可以设计一个位移与力转换系数CF，把位移命令转化为力命令，以使得试验加载系统采用力控制模式工作。同时通过布设在试验结构上的高精度位移传感器，采集结构的位移反应(反馈量)di+1'，并通过外环位移控制器实现目标位移，这就是本文试验方法的思路，如图1所示。值得说明的是，小位移加载的大刚度结构一般处于线弹性状态，若结构进入非线性状态，则可以切换成传统的位移控制加载模式。

图1 力和位移混合控制拟动力试验方法原理图Fig.1 Block diagram of the PSD tests under mixed force and displacement control

2 位移控制器设计

目标位移需要一个反馈控制来实现，而位移控制器是实现这一过程的重要环节，它的品质好坏决定了试验能否顺利进行。因此，需要设计一个合适的位移控制器以消除控制系统的控制误差。常用的控制器有PID控制、滑动模态控制、自适应控制等。本文采用PI控制，图2为带PI控制器的混合控制方法试验框图，其中的虚线部分为PI控制器，KP，KI分别为控制器的比例增益和积分增益;TC(s)为控制器的传递函数;TA(s)为包括力控制器的液压伺服作动器的传递函数;TE(s)为试验结构的传递函数，TE(s)=1/K，K为试验结构的刚度矩阵;s为拉普拉斯算子。

TA(s)可以简化为二阶传递函数［12］:

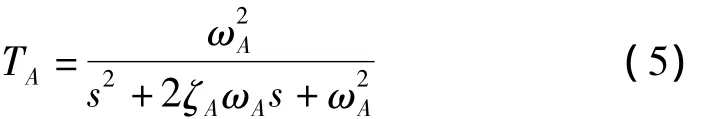
式中:ζA和 ωA分别为作动器的等效阻尼比和等效圆频率。

图2中反馈控制系统的开环传递函数为:

图2 带PI控制器的混合控制方法试验框图Fig.2 Block diagram of the PSD tests under mixed force and displacement control with PI controller

其闭环传递函数为:

根据劳斯判据，由式(7)可以得到反馈控制系统的稳定条件为:

对于线性系统，当CF=K时，稳定条件为:

对于软化系统，当CF采用结构的初始刚度时，式(9)的稳定界限偏于保守。

由拉普拉斯终值定理，可求得系统在单位阶跃位移命令下的稳态误差为:

从式(10)可以看出，无论CF取何值，即使结构进入非线性状态，单位阶跃命令输入下系统均无稳态误差产生。

文献［13］采用了PD控制器对等效力命令进行控制，通过增加开环增益KF=(1+KP)/KP的方法消除系统在单位阶跃命令下的稳态误差。这种方法对于线性结构的试验非常有效，但当结构进入非线性状态时，需要识别结构的刚度以重新计算CF和KF值才能保证系统不会出现稳态误差，这通常是非常困难和耗时的。相比较而言，采用PI控制器，CF采用结构的初始刚度，即使结构进入非线性，仍能保证系统无稳态误差产生。

3 数值模拟

数值模拟由Matlab软件在时域中完成，反馈控制系统采用数字控制，采样频率为1000Hz。试验加载系统的二阶传递函数采用零阶保持器法离散。小位移加载的大刚度结构一般处于线弹性状态，故对线弹性结构进行力和位移混合控制拟动力试验的数值模拟。图3所示的单自由度结构为研究对象，其中数值子结构的参数为:质量MN=2.533 ×103kg，刚度KN=0，阻尼系数CN=0。试验子结构为线弹性弹簧，刚度 KE=10 kN/mm，阻尼系数 CE=0，结构的自振周期为0.1 s，弹性恢复力RE可由KE和弹簧变形求出。

图3 单自由度结构简图Fig.3 Schematic of SDOF structure

3.1 单步阶跃反应

系统在1mm单步阶跃命令下的位移响应如图4所示，其中，KP=0.1，CF=KE。从图中可以看出，随着KI的增大，结构位移响应速度加快，稳态误差逐渐减小。当KI=15/s时，稳态误差为零，位移响应能很好地跟踪位移命令，而继续增大则出现超调现象。KI的稳定界限值为552.92/s。

3.2 自由振动反应

结构自由振动反应如图5所示。初始位移为1mm，初始速度为0。控制器参数采用由单步阶跃响应得到的最优值KP=0.1，KI=15/s。可以看出采用混合控制试验方法计算得到的结果与解析解结果吻合的非常好，并且每步位移响应均能很好地跟踪其位移命令，可以说明该方法是可行的。

图4 单步阶跃命令下的位移响应Fig.4 Step displacement response of the SDOF

图5 自由振动位移反应Fig.5 Free-vibration displacement response of the SDOF

4 试验验证

4.1 小位移正弦波加载试验

大刚度结构试验，位移反应往往比较小，需要对小位移进行加载与测量，那么对试验设备的精度要求比较高。本次试验在哈尔滨工业大学力学与结构试验中心完成。试验对象为弹簧，其刚度为0.03 kN/mm。相比作动器的刚度，该弹簧的刚度较小，但并不影响该试验的验证。整个试验采用了基于dSPACE控制的加载系统，系统的采样频率为1000Hz。加载设备为北京富力通达公司的FTS作动器，其位移与力量程分别为±100mm和±30 kN，外接高精度位移传感器的量程为±5mm。加载的正弦波幅值为0.01mm，通过经验试凑法得到位移控制器参数为 KP=10，KI=0.6/s，CF取弹簧刚度，作动器采用力控制，试验装置及结果如图6所示。

从图6中可以看出，当进行小位移加载时，作动器的位移响应中噪声比较大，不能很好地实现位移命令，而外接高精度位移传感器能较好地实现位移命令。可以看出作动器的位移传感器精度要比外接位移传感器的精度低，那么采用传统的位移控制方法将无法完成小位移的加载，而采用混合控制方法则可以实现小位移的加载和测量，这也体现出该方法的优点。

图6 正弦加载位移反应Fig.6 Displacement responses from sinusoidal test

图7 防屈曲支撑阻尼器(BRB)拟动力试验装置Fig.7 PSD test setup of BRB

4.2 地震动激励拟动力试验

试验在哈尔滨工业大学力学与结构试验中心完成。试验对象为设置了防屈曲支撑阻尼器的单自由度结构，模拟该结构在地震作用下的反应，试验装置如图7所示。试验的控制和加载设备采用MTS公司的Flex Test GT控制器和Schenck作动器，作动器的位移与力量程分别为±250mm和±630 kN，外接高精度位移传感器的量程为±5mm。数值子结构的参数为:质量MN=60×103kg，刚度KN=0，阻尼比取为5%。试验子结构为防屈曲支撑阻尼器，其水平抗侧刚度为26.87 kN/mm，可以看出该结构属于大刚度结构。地震动输入为El Centro(NS，1940)加速度记录，峰值加速度为0.05 g。积分时间步长为0.01 s，每个时间步长持续0.5 s，积分方法采用中心差分法。试验分别采用了传统拟动力、内环分别为力控制和位移控制的混合控制拟动力等三种方法。

4.2.1 内环力控制的混合控制方法与传统拟动力方法试验结果对比

内环为力控制时，通过经验试凑法得到外环位移控制器参数为 KP=1.4，KI=23/s，CF取支撑水平抗侧刚度，混合控制方法与传统拟动力方法得到的试验结果如图8所示。从图8(a)中可以看出，混合控制方法得到的结构位移反应小于传统拟动力的试验结果，造成这样的原因主要有:① 作动器与试件之间的连接存在间隙;②连接部的变形;③ 地梁的滑移。相比较而言，由混合控制方法得到的试验结果更能反映结构的真实位移反应。从图8(b)、图8(c)可以看出由传统方法得到的作动器位移响应和结构反力时程均要比混合控制方法得到的结果大，但在结构初始位移为零时，前者得到了非零的结构初始反力，这与实际情况不符。图8(d)、(e)分别为由传统拟动力方法及混合控制方法得到的支撑滞回曲线。可以看出传统拟动力方法得到的滞回曲线较饱满，这跟连接间隙和连接部的变形有关。从控制效果来看，两种方法中的位移响应均能很好地跟踪位移命令，但传统拟动力方法的控制效果略差于混合控制方法，图8(f)、图8(g)所示。同时，传统拟动力方法的控制对象为作动器的位移响应，而作动器的位移响应无法反映结构的真实位移。混合控制方法的控制对象为结构的位移反应，可以使得结构实现期望的位移命令，试验结果更准确。从图8(h)可以看出，在混合控制方法中作动器的力响应能很好地跟踪其命令。

从上述试验结果及分析可以得出，内环采用力控制的混合控制拟动力方法优于传统拟动力方法，它的试验结果更准确。

图8 混合控制方法与传统拟动力方法的试验结果Fig.8 Test results obtained by the mixed control method and conventional method in PSD test

图9 内环为力控制和位移控制的混合控制方法的试验结果Fig.9 Test results obtained by force and displacement in the mixed inner control loop in PSD test，respectively

4.2.2 内环力控制与内环位移控制的混合控制方法试验结果对比

内环为位移控制时，通过经验试凑法得到外环位移控制器参数为KP=1.8，KI=26/s，内环分别为力控制与位移控制得到的试验结果如图9所示。从图9(a)中可以看出，内环采用位移控制与采用力控制得到的结构位移反应相差较大，而等效力控制方法与内环采用力控制得到的试验结果吻合得很好。图9(b)可以看出两种控制方法得到的作动器位移响应也相差较大。图9(c)为试验结构的反力时程。可以看出，内环采用位移控制时，结构初始位移为零时就存在非零的反力，与实际情况不符。图9(d)为两种控制方法得到的支撑滞回曲线，可以看出两者的形状相似。从图8(g)和图9(e)中可以看出，两种方法中的结构位移反应都能很好地跟踪位移命令，但采用力控制得到的结构位移反应更平滑。对比图8(h)和图9(f)可以看出，作动器采用力控制的控制效果要好于采用位移控制的控制效果，后者始终存在稳态误差，这种误差直接导致了测得结构的反力存在误差，进而导致求解的结构位移存在误差。从图9(g)和图9(h)也可以看出采用力控制时作动器的力与位移响应更平滑。作动器的控制效果与其控制精度与测量精度有关，当测量精度低于控制精度时，作动器的控制效果就比较差，反之则控制效果好。从试验结果可以看出，结构位移反应最大值约为作动器位移量程的1/125，反力最大值约为作动器力量程的1/10，可见作动器的力测量精度要高于位移测量精度，并且力测量精度通常也高于其控制精度，作动器采用力控制的控制效果要好于采用位移控制的控制效果，这样前者得到的结构反力更精确，计算的结构位移反应也更精确。

从上述试验结果及分析可以得出，内环分别采用力控制和位移控制的混合控制方法都能完成拟动力试验，但前者得到的试验结果更精确。

5 结论

提出了内环为力控制、外环为位移控制的混合控制拟动力试验方法，并从数值模拟和试验验证两个角度来论证了该方法的可行性，结论如下:

(1)选取合理的PI控制器参数，并采用结构的初始刚度作为位移与力转换系数，该方法具有非常好的稳定性和精度。

(2)该方法可适用于大刚度结构拟动力试验，可以实现小位移的精确加载和测量。

(3)大刚度结构试验中，该方法优于传统拟动力试验方法，也优于加载设备采用位移控制的混合控制方法。

值得指出的是，当试验结构的刚度下降时，可以由力控制转换成位移控制来继续完成试验加载。那么需要确定一个合理的转换控制指标，以使得从力控制到位移控制实现平滑转换而不影响试验结果。对于位移控制器参数的整定，需要依据合理的方法以便更快捷、准确地确定最优的参数值，使得反馈控制系统性能达到最佳状态。同时，由于试验中存在各种误差，导致试验结果也存在误差，如何减小试验中的误差是该混合控制方法的一个研究重点。此外，对于多自由度结构拟动力试验，该混合控制方法的精度和稳定性也需进一步研究。

［1］Mahin S A，Shing P B.Pseudodynamic Method for Seismic Testing［J］.Journal of Structural Engineering，1985，111(7):1482－1503.

［2］Aktan H M.Pseudo-Dynamic Testing of Structures［J］.Journal of Engineering Mechanics，1986，112(2):183 －197.

［3］Takanashi K，Nakashima M.Japanese Activities on On-Line Testing［J］.Journal of Engineering Mechanics，1987，113(7):1014－1032.

［4］Shing P B，Nakashima M，Bursi O S.Application of Pseudodynamic Test Method to Structural Research ［J］.Earthquake Spectra，1996，12(1):29 －56.

［5］刘 季，李 暄，张培卿.大刚度结构力控制拟动力实验方法［J］.地震工程与工程振动，1996，16(4):55 －59.LIU JI，Li Xuan，ZHANG Pei-qing.Study on pseudodynamic test method under force control used in stiff multi-storey structures［J］.Earthquake Engineering and Engineering Vibration，1996，16(4):55 －59.

［6］李 暄，刘 季，田石柱.结构拟动力试验力控制实现技术［J］.地震工程与工程振动，1997，17(1):49 －53.LI Xuan，LIU Ji，TIAN Shi-zhu.Structural pseudo-dynamic testing technology by force control ［J］. Earthquake Engineering and Engineering Vibration，1997，17(1):49 －53.

［7］王凤来，陈再现，王焕定，等.制高阶单步力控制拟动力试验方法研究［J］.地震工程与工程振动，2008，28(6):233－238.WANG Feng-Lai，CHEN Zai-Xian，WANG Huan-ding，et al.High-order single-step method for force-control pseudodynamic test［J］.Earthquake Engineering and Engineering Vibration，2008，28(6):233 －238.

［8］Pan P，Nakashima M，Tomofuji H.Online test using displacement-force mixed control ［J］. Earthquake Engineering and Structural Dynamics，2005，34:869－888.

［9］Nakata N，Spencer，Jr B F，Elnashai A S.Mixed load/displacement control strategy for hybrid simulation［A］.4thInternational Conference on Earthquake Engineering，Taipei，2006:94－103.

［10］Sivaselvan M V，Reinhorn A M，Shao X Y，et al.Dynamic force control with hydraulic actuators using added compliance and displacement compensation［J］.Earthquake Engineering and Structural Dynamics，2007:1 －10.

［11］Kim H K，Stojadinovic B，Yang T Y.A schellenberg alternative control strategies in hybrid simulation［A］.2ndEFAST Workshop and 4thInternationalConference on Advances in Experimental Structural Engineering［C］.Ispra Italy，2011，1－14.

［12］Jung R Y.Development of real-time hybrid test system［D］.Colorado，USA:University of Colorado，2005.

［13］Wu B，Wang Q Y，Shin P B，et al.Equivalent force control method for generalized real-time substructure testing with implicitintegration ［J］. Earthquake Engineering and Structural Dynamics，2007，36:1127－1149.