磁爆加载初始阶段薄壁金属管冲击变形研究

夏 明，黄正祥，顾晓辉，张先锋

(1.南京理工大学 智能弹药技术国防重点学科试验室，南京 210094;2.总参工程兵科研三所，洛阳 471023)

磁爆加载弹药技术是目前提升常规武器毁伤效能的新概念技术之一，其突破了传统的爆炸驱动毁伤元的模式，利用爆轰到强磁场过程较高的能量转化效率和易于控制的磁场聚焦方法，可形成多种形态的高效毁伤元，进而对目标进行打击。该技术可使炸药的能量利用率提高30%，进而大幅提高弹药的毁伤能力。磁爆加载的能源是磁爆压缩发生器(即FCG)，它是一种可以把炸药的化学能转换成电磁能的脉冲能源装置［1－5］，已广泛应用于军事和尖端科研领域，如电磁发射(EML)［6］，高能量密度物理(HEDP)试验［7］等。而将FCG应用于磁爆加载弹药，通过FCG作用驱动成型装置，产生强磁场，进而加载内置金属结构，并使其变形甚至熔化，最后形成高速熔融态毁伤元对目标进行作用的研究，还未见报道。

本文建立了磁爆加载初始阶段薄壁金属管受磁载荷冲击变形的理论模型，并在此基础上，利用数值仿真方法，研究了薄壁金属管的冲击变形特征，并对结果进行试验验证，为进一步探索薄壁金属管在磁爆加载后续阶段中的物理过程提供了指导。

1 理论模型

1.1 磁爆加载的作用过程

磁爆加载作用过程可分为初始阶段和磁通压缩两个阶段，本文主要针对磁爆加载的初始阶段进行分析。在初始阶段，FCG由脉冲电容器供电，产生种子电流和初始磁通，同时对串联在回路中的驱动成型装置供电，产生随种子电流上升的磁场和脉冲磁动力，并作用于内置薄壁金属管的通流线圈，使薄壁金属管发生冲击变形;而当种子电流到达峰值时，FCG被起爆，爆炸开关闭合，进入磁通压缩阶段。

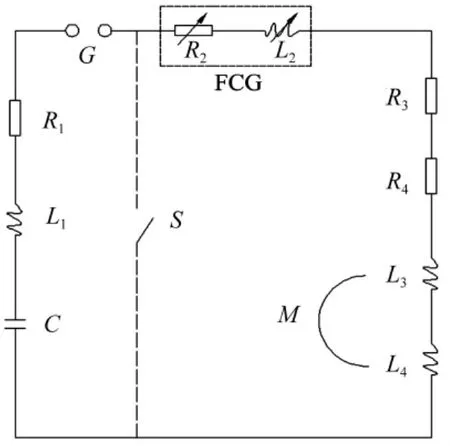
图1 电路模型Fig.1 The circuit model

磁爆加载电路如图1所示，S为FCG的爆炸开关，C 为脉冲电容器，G 为间隙开关，R1，R2，R3，R4和 L1，L2，L3，L4分别为传输线、FCG、驱动成型装置和内置薄壁金属管通流线圈的电阻和自感，M为驱动成型装置与内置金属管通流线圈间互感。

1.2 加载电流分析

在初始阶段，脉冲电容器放电，产生种子电流，电路可简化为RLC电路。设电路元件为理想元件，U，R，L，C，I分别为电容器充电电压，电路总电阻、电感、电容和电流，且加载电路各元件的电阻较小，约数十mΩ，而电感和电容约为数十μH或μF，多在一个量级内，因此，通常满足振荡电路条件，则总电流I可表示为:

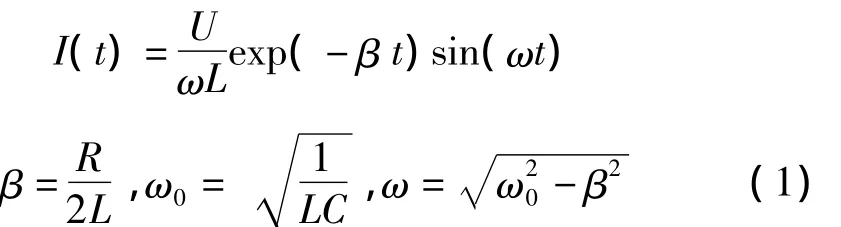
总电阻R可表示为:

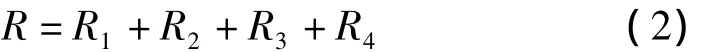
由于驱动成型装置和FCG是由多匝线圈绕制而成，计算其脉冲电流作用下的电阻，不仅需要考虑电流趋肤效应，还要计算线圈匝间邻近效应对电阻的影响。而其他元件的线圈匝数较少或本身临近效应较弱，仅考虑趋肤效应，因此，各元件的电阻可表示为［8］:

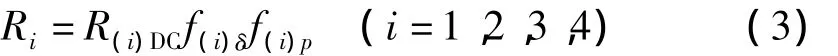
式中:R(i)DC为回路各元件的直流电阻，f(i)δ与f(i)p为趋肤效应和临近效应修正系数。

电容器对磁加载电路的放电过程，各元件的电感变化较小，而驱动成型装置与内置薄壁金属管的通流线圈之间为反向串联互感的耦合模式，因此，总电感L可表示为:

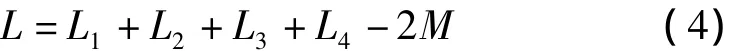
将式(2)、(4)的结果代入式(1)，就可得到磁加载电流I。

1.3 磁动力分析

根据磁加载电流I，结合驱动成型装置的结构，可求得驱动成型装置的电流密度矢量。引入满足Maxwell方程组的矢量磁位函数，定义其满足下式:

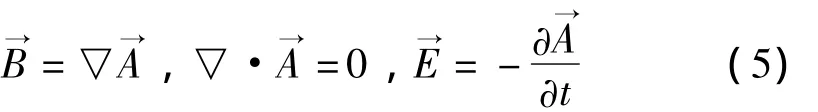
若忽略位移电流，并设磁场中的介质为电磁各向同性，Maxwell方程组变为仅含有矢量磁位函数和电流密度矢量的微分方程:

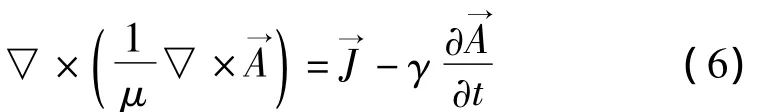
在通流区、感应区和无源区三个不同的计算区域，求解所有的定解问题，获得矢量磁位函数;再根据方程(5)，求解磁感应强度矢量;最后将的结果叠加，得到整个区域的磁场解。根据薄壁金属管任意时刻t、任意位置x磁感应强度的分布，可得到相应的磁动力:

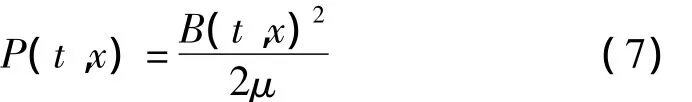
1.4 金属管的冲击变形分析

根据磁动力在薄壁金属管不同时刻和位置的分布，作为加载条件，结合金属材料冲击加载下的Mie-Grüneisen状态方程和Johnson-Cook材料模型，就可分析薄壁金属管的变形过程［9］。Mie-Grüneisen方程定义压缩和膨胀材料的压力为:

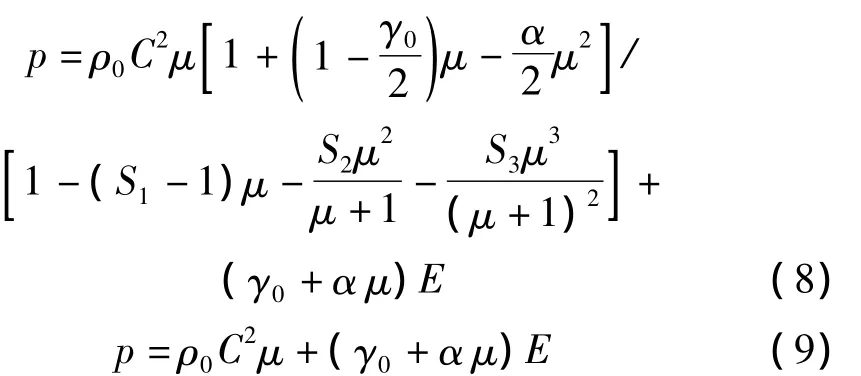
其中:C 为体积声速;S1，S2，S3是 Us－Up曲线斜率系数;γ0是 Grüneisen 常数;μ = ρ/ρ0－1;a 是 γ0的一阶体积修正系数。

Johnson-Cook材料模型方程为:

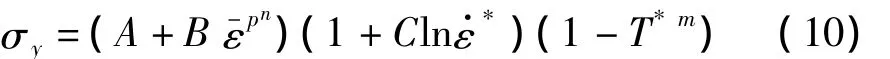
式中:ε－p为等效塑性应变为参考应变率，为相对温度，T*=(T－Troom)/(Tmelt－Troom);A为屈服应力;B为应变硬化系数;n为应变硬化指数;C为应变率相关系数;m为温度相关系数。

2 薄壁金属管的冲击变形仿真研究

按照理论模型，利用磁场分析和动力学分析的MAXWELL，AUTODYN软件联合仿真，得到了图2中驱动成型装置，在种子电流峰值约30 kA时，加载两种薄壁金属管的磁动力分布和冲击变形过程。

图2(a)中驱动成型装置采用4mm2的单芯铜导线绕制，20层，层间并联，每层35匝;其中心内置了外绕线圈的薄壁金属管。如图2(b)所示，采用三角形网格和2D轴对称的形式进行有限元建模，并对所关心的金属管与驱动成型装置临近区域的网格进行了细化。

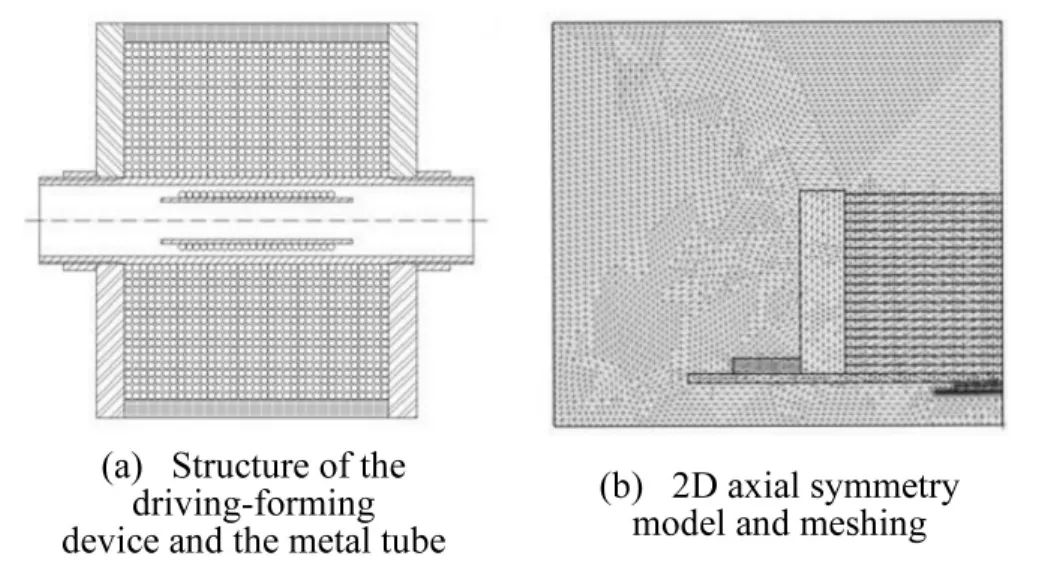
图2 驱动成型装置的结构和网格划分Fig.2 Structure of the driving-forming device and the meshing

图3 两种金属管Fig.3 Two kinds of the thin-walled metal tube

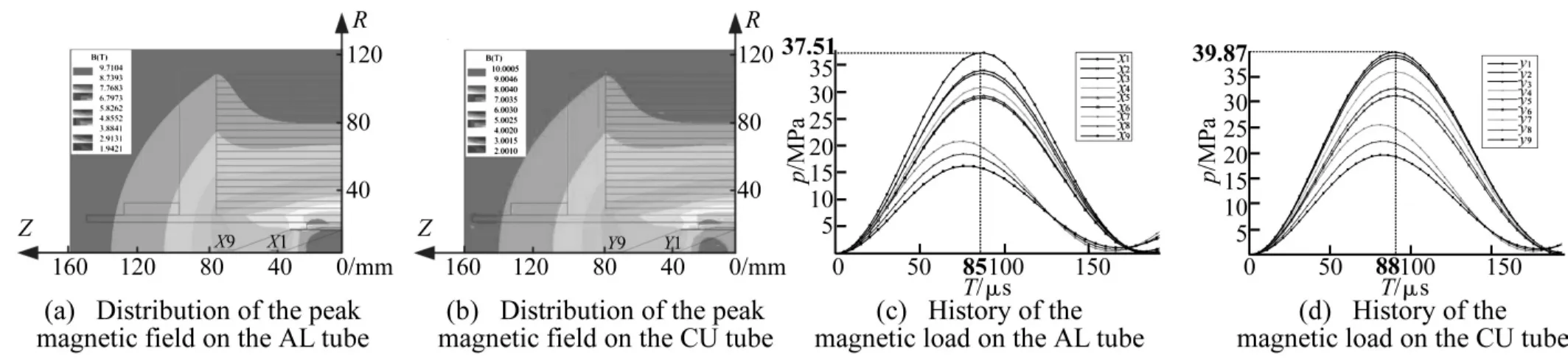
图4 磁场峰值分布和磁动力时间历程Fig.4 Peak distribution of fields and history of magnetic loads

两种薄壁金属管结构，见图3(a)和图3(b):2024－T351铝管，外径30mm，壁厚0.5mm，长度60mm;OFHC 铜管，外径30mm，壁厚0.3mm，长度60mm。

驱动成型装置和薄壁金属管都为轴对称结构，因而，磁场和磁动力分布的计算，相应采用了2D轴对称模型。种子电流达到峰值时的磁场分布见图4(a)、图4(b);磁动力的各采集点沿金属管外壁从中截面至口部，依次分别为X1～ X9和Y1～Y9，铝管对应X标号的采集点，铜管对应Y标号的采集点，磁动力在各采集点的时间历程分布见图4(c)、图4(d)。

在约30 kA峰值的种子电流驱动下，驱动成型装置使铝管和铜管的中截面位置分别产生了约37.51 MPa和39.87 MPa的峰值磁动力。两管都产生了塑性变形，铝管和铜管的变形对撞部分各自获得了约430 m/s和680 m/s的轴向速度。铜管与铝管的变形过程相似，以铜管的变形过程为例进行说明。见图5，88 μs为磁动力峰值点，峰值到达前，变形的管壁向轴线运动，并不断加速;峰值过后，磁动力开始减小，而管壁仍在加速;约100 μs时，管壁在轴线方向形成碰撞，使碰撞部分获得轴向速度，碰撞结束后，金属管的压垮形态随之固定。

由仿真结果发现:

图5 铜管变形过程仿真结果Fig.5 Deformation process of the copper tube

(1)磁动力加载时呈脉动变化，且不同位置磁动力峰值差异较大。沿金属管母线方向，磁动力从中心至口部依次减小。

(2)通流线圈与驱动成型装置耦合产生的磁感应强度，大于金属管口部感应产生的磁感应强度。如图4(a)和图4(b)所示，在金属管与通流线圈口部的接触位置，铝管和铜管的磁场峰值分别达到了10.0 T和9.7 T，其变形效果比口部更明显。

(3)薄壁金属管在磁动力加载下的变形趋势与其外侧包裹不同厚度的炸药爆炸加载的变形趋势相似，具有类似的冲击变形特征，由于冲击压缩引起了剪切应力，形成了管壁上沿轴向的褶皱，并伴有一定程度的剪切扭转。

(4)磁动力第一峰值的到达时间和幅值对薄壁金属管的变形过程具有决定作用。如图5所示，磁动力第一峰值时，金属管的变形接近完成，若第一峰值的到达时间比管壁自由运动时间短，则管壁可获得较充分加速，压垮管壁的碰撞效应更明显;同时，只有磁动力第一峰值超过金属管的屈服极限，才能发生塑性变形。

3 薄壁金属管的冲击变形试验研究

为获得薄壁金属管的磁载荷冲击变形实际特征，并检验理论模型和数值仿真的效果，进行了磁爆加载初始阶段约30 kA峰值种子电流驱动下，驱动成型装置加载两种材料和结构薄壁金属管的冲击变形试验。

3.1 试验器材和设置

主要试验器材包括:① 脉冲电容器:MWF50－8型10台，每台额定电压50kV，8 μF;② 驱动成型装置1台，其结构见图2;③ FCG 1台;④ 间隙开关1个;⑤示波器 1台;⑥ Rogowski线圈 1个，灵敏度 20.67 kA/V;⑦ 分流器1个，额定电流50 kA;⑧ 衰减器2个，10 dB;⑨ 薄壁金属管2个，结构见图3。

以10台脉冲电容器并联提供电能输出，将主要试验器材按照图6所示连接。Rogowski线圈和分流器测量的波形，经衰减器输入屏蔽柜中的示波器，示波器采集波形后，再将测量数据转存计算机。

图6 试验设备布置Fig.6 Arrangement of the experiment equipments

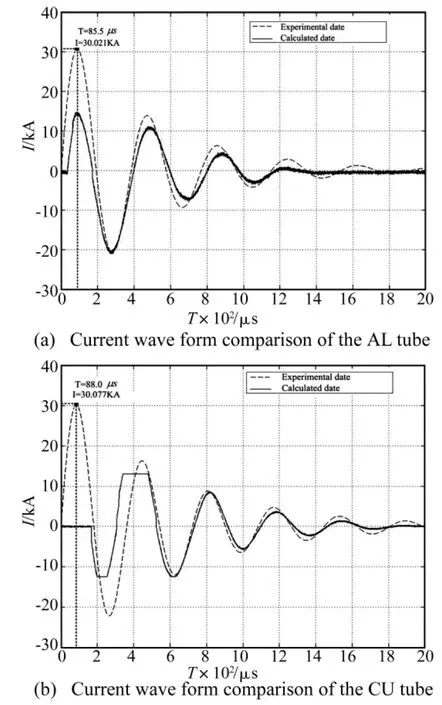
图7 理论计算电流数据与试验数据的对比Fig.7 Comparison of the wave form between calculation and experiment

3.2 试验结果

对铝管和铜管进行试验时，电容器电压分别达到了25.0kV和28.0kV，而带磁芯的Rogowski线圈发生了磁饱和，结果失真，只获得了分流器的测量数据。将电流理论计算结果与实测电流数据进行了比较，见图7。在脉冲电流的初始段二者有明显差异，但其余数据点基本吻合，这是分流器本身剩余电感和示波器记录起始点设置而产生的测量误差所致，因而，测量误差不影响电流第一峰值的结果。

将仿真得到的薄壁金属管终态变形与试验结果进行对比，见图8和图9，铝管发生了口部开裂，与仿真结果有一定差异，但变形趋势一致，而铜管的二者形态基本一致，数值仿真结果与试验结果相吻合，理论模型也较好地反映了磁爆加载薄壁金属管的冲击变形过程。同时，管壁表面由于电流焦耳热效应，图8和图9中圆环圈出的部分开始发生金属熔化现象，在磁爆加载的后续阶段，热效应的影响将更加明显。

图8 铝管变形与仿真结果的对比Fig.8 Comparison of calculated and experiment deformation with the AL tube

图9 铜管变形与仿真结果的对比(半幅)Fig.9 Comparison of calculated and experiment deformation with the CU tube(half part)

4 结论

(1)建立的磁爆加载初始阶段薄壁金属管受磁载荷冲击变形的理论模型能清晰地反映这一物理过程，且理论分析和数值仿真结果与试验吻合较好。

(2)薄壁金属管在磁动力加载下的变形特征与其外侧包裹高能炸药爆炸加载的变形相似，具有类似的冲击变形特征。

(3)磁动力加载位置分布及其第一峰值的时间进程直接影响薄壁金属管的最终变形，通过对驱动成型装置的设计，可以控制加载磁动力，获得所需的终态构型。

［1］Knoepfel H.Pulsed high magnetic fields［M］.North-Holland，Amsterdam，1970:1－21.

［2］Fowler C M，Altgilbers L L.Magnetic flux compression generators:a tutorialand survey［J］.Electromagnetic Phenomena，2003，3(11):306 －357.

［3］Freeman B L，Altgilbers L L.Development of small tapered stator helical magnetic flux compression generators［J］.Electromagnetic Phenomena，2003，3(11):366 －371.

［4］Cavazos T C.Flux compression generator develop-ment at the air force research laboratory［C］.Sympo-sium of IEEE Pulsed Power Conference，2005:453－456.

［5］Appelgren P.Experiments with and modeling of explosively driven magnetic flux compression generators［D］.School of electrical engineering space and plasma physics royal institute of technology Stockholm，Sweden，2008.

［6］Peterson C R，Fowler C M.Rail gun powerd by an integral explosive generator［R］.LA-UR-79 －2220，1979.

［7］孙承纬.电磁加载下的高能量密度物理问题研究［J］.高能量密度物理，2007(01):41－46.SUN Cheng-wei.Research of HEDP with magnetic load［J］.High Energy Density Physics，2007(1):41 － 46.

［8］Altgilbers L L，Brown M D J，Grishnaev I，et al.Magnetocumulative generators［M］.New York:Springer，2000:132－133.

［9］Meyers M A.Dynamic behavior of materials［M］.John Wiley and Sons，Inc，1994:150 －170.