水石流冲击信号能量分布试验研究

陈洪凯，鲜学福，唐红梅，张玉萍，何晓英，文光菊，唐 兰

(1.重庆交通大学 岩土与地质工程系，重庆 400074;2.重庆大学 西南资源开发及环境灾害控制工程教育部重点实验室，重庆 400044)

泥石流冲击力是实施泥石流防治结构设计的荷载依据，属于阵发性可变荷载。由于泥石流体内固相物质颗粒粒径离散性大，且每一种粒径与浆体之间的作用方式存在显著差异［1］，增大了实施泥石流运动机理与冲击荷载研究的难度。Bagnold［2］通过转筒剪切试验提出了颗粒之间法向力和切向力计算公式;Savage［3］通过水槽试验揭示了无粘性颗粒流的运动特性，分析了颗粒流边壁摩擦、龙头跃动和颗粒弹跳等动力学效应;Takahashi［4］将泥石流体视为剪胀流，通过水槽试验建立了泥石流头部颗粒动力分选力学机制，发现比团聚体直径大的颗粒向上部移动，而比团聚体小的颗粒则向下运动;Arattano等［5］通过水槽试验探讨了泥石流能量波问题;Iverson等［6］采用流变理论提出了库仑混合物模型，分析了颗粒流中具有较大摩擦作用的头部与其后部流化碎屑之间的相互作用;Valentino等［7］进行了颗粒流水槽试验，采用摄像法记录了颗粒流形成及运动过程，并借助于离散元软件PFC2D系统模拟了颗粒流水槽试验，获取颗粒流冲出距离和冲击力频谱特性;Armento等［8］运用一维DAN－W模型分析了泥石流的动力特性，运用二维FLO－2D模型分析了泥石流在沉积扇上的迁移变化规律;费祥俊等［9］采用泥沙运动力学方法分析了泥石流冲击问题;吴积善［10］根据蒋家沟泥石流1974－1975年冲击力测试资料，得到泥石流冲击动压力的修正公式，并通过实际观测将泥石流冲击力谱提炼为锯齿形脉冲、矩形脉冲和尖峰形脉冲三种;魏鸿［11］通过室内试验建立了泥石流龙头对坝体的冲击力计算公式，周必凡［12］基于颗粒流模型建立了粘性泥石流阻力方程和匀速流动方程，Chen等［13］分析建立了计算滑坡诱发型泥石流流量的计算公式;张宇等［14］引入泥石流体微元概念，将泥石流冲击力作为非平稳信号，采用Hilbert变换进行时频处理确定冲击作用时间;梁金培等［15］和巴仁基等［16］通过对泥石流现场调查从泥石流运动形迹推测泥石流冲击荷载;陈洪凯等［17－18］从固液两相流理论出发探讨了泥石流冲击力计算问题。

综上所述，泥石流冲击荷载研究目前仍然停留在惟像的宏观实验研究阶段，以获得泥石流平均冲击力为目的，缺乏对泥石流冲击信号的细观分析，本文针对水石流室内冲击试验结果，采用小波变换法探讨泥石流冲击信号的能量分布问题，为实施泥石流冲击动力学精细化研究提供科学依据。

1 泥石流冲击模型试验［19］

(1)试验模型设计

图1 泥石流冲击试验模型Fig.1 Experimental model of debris flow shock testing

在重庆交通大学泥石流动力模型试验场建造沟谷泥石流试验模型(图1)，模型主沟长度9.0 m、高差3.6 m、沟床平均坡度 26°;泥石流沟由水泥砂浆现场浇筑而成，沟槽较光滑;沟源为水源箱，尺寸1.0 m(长)×1.0 m(宽)×1.5 m(高)，储水量 1.5 m3;水源箱出口处设置碎石漏斗，其高度0.5 m，顶部直径0.6 m，底面直径0.4 m，漏斗底部阀门设置为抽板式，开口大小可以根据试验中固相比的大小进行调整;泥石流沟口安置HS200型动态应力传感器。

(2)试验工况

本文重点分析不同固相粒径及不同固相比条件下泥石流的冲击荷载，属于水石流室内模型试验。固相粒径分 A(粒径0.3 ～0.8 cm)、B(粒径0.8 ～1.5 cm)、C(粒径 1.5 ～ 3.0 cm)三组，固相比分 0.02、0.08、0.16、0.20 和0.25 共五种情况，按照正交组合方式拟定15种试验工况(表1)。

表1 泥石流冲击试验工况Tab.1 Testing conditions of debris flow shock

(3)测试方法与内容

按照每个工况实施3次试验，针对15种试验工况，共实施了40余组泥石流冲击试验，每次试验持续时间控制在10～20 s范围内。采用Fastcam-ultima1024型高速摄像机连续记录泥石流运动形态，采用HS200型动态应力传感器和多通道动态应变仪连续记录泥石流冲击荷载变化过程。由于模型试验得到的数据量较大，有85000多个，本文仅选用固相比为0.16的A－3，B－3和C－3三个试验工况的测试结果分析水石流冲击信号的能量分布特性，该冲击信号为泥石流沟流通区出口处的正面冲击力。动态应变仪的采样频率为0.01Hz。

2 水石流冲击信号处理

图2为B－3试验工况获得的水石流冲击谱，是固相颗粒和粒间流体冲击信号的宏观表象，可采用离散小波分层分解方法提炼冲击信号。由于db小波具有阶数越高规则性越显著的特性，原始冲击信号经过多层高、低频逐层分解可得到最后的低频信号f8和一系列频率渐变的高频信号g1～g8，其中f8可以反映原始信号整体状态，而高频信号体现了原始信号中夹杂不同频段的噪声信号，实现原始信号的小波分析。本文利用db8小波基对图2试验结果进行8层小波分解，分解后的九个频率段如图3所示。九个频率段的频率范围分别为 0 ～ 0.195Hz，0.195 ～ 0.391Hz，0.391 ～0.781Hz，0.781 ～ 1.563Hz，1.563 ～ 3.125Hz，3.125～6.25Hz，6.25 ～12.5Hz，12.5 ～25Hz和25 ～50Hz，据此可进行水石流冲击信号能量分布特性分析。

设水石流冲击荷载信号的总能量为E0，则:

式中，f(t)表示为经分解后得到的低频信号;g(t)表示经分解后得到的高频信号。为便于分析，用g0(t)代替f(t)，并考虑到小波的正交性［20］，则水石流冲击总能量可简化为:

波纹管的波纹结构有采用2个不同圆弧段和分别采用圆弧段、平直段2种方式。目前应用较多的是圆弧段与平直段相接的方式。文中即模拟圆弧与平直段相接的波纹管，并认为圆管内充满流动的流体，具体物理模型如图1所示。模型长度为180mm，直径为20mm。流体由左侧流入波纹管，由于流动为单相流动，不考虑重力对流动的影响。

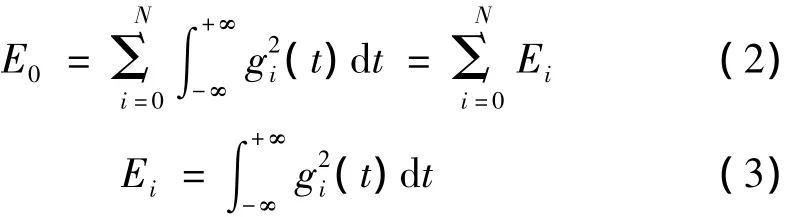
由此可得不同频段上水石流冲击能量分布:

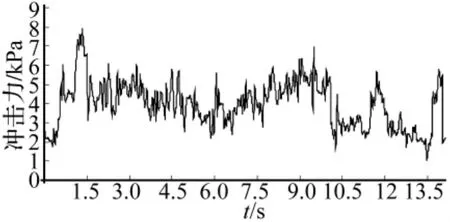
图2 B－3试验工况水石流冲击谱Fig.2 Shock spectra of the B －3 testing condition for non-viscosity debris flow

3 水石流冲击信号能量分布特征

同理，可得B－3和C－3试验工况的水石流冲击信号频率段重构信息，固相比为0.16的三个试验工况在不同频率段的冲击能量分布状况如图4所示。可见，本实验条件下水石流90%以上的冲击能量分布在低频(频段一)部分，中、高频段冲击能量分布仅占10%左右，水石流中粒径越小，中、高频段的冲击能量越小;中、低频段的水石流冲击能量总体呈现衰减分布趋势，但在频段三(0.391 ～0.781Hz)和频段六(3.125～6.25Hz)出现较显著的峰值，其中频段三的峰值强度略高于频段六;水石流中固相颗粒的粒径越小，低频段至高频段的冲击能量衰减速度越慢。

图4 水石流冲击信号能量分布Fig.4 Energy distribution of shock signal for non-viscosity debris flow

4 讨论

(1)本文研究对象为水石流，未考虑浆体粘度对冲击特性的影响，所实施的室内模型试验未考虑相似比，其本质仍然是定性揭示泥石流冲击特性的水槽类模型试验，所揭示的泥石流冲击信号与实情必然存在较大差异。但是，遵循对科学问题逐步探索原则，本文实验结果也具有一定科学意义。

(2)实验表明，水石流冲击能谱从低频到高频非线性衰减，约90%的冲击信号能量主要位于0.195Hz以下的低频段，其余中、高频段占10%左右，该结论初步表明，在泥石流防治结构设计考虑动力效应时应重点考虑低频段冲击荷载。

(3)实验表明，水石流冲击能量分布曲线中，在频段一、三、六处出现显著能量峰，峰值强度逐渐衰减，这可能是泥石流阵性的宏观表象，与吴积善等对蒋家沟泥石流冲击特性现场测试揭示的泥石流运动规律［10］具有谨慎的对比性，对于探索泥石流龙头冲击强度［11，21］、压胀机理［22］具有一定启示作用，换言之，水石流也存在阵流特征，但其跃动周期、峰值强度与粘性泥石流必然存在显著差异。

(4)实验表明，为全面揭示泥石流冲击特性，应系统实施不同浆体粘度、固相比、粒径级配组合条件下的大尺度敏感性水槽试验，探索泥石流冲击信号能谱特征，合理揭示泥石流冲击能量所处频段、跃动周期及峰值强度与泥石流阵性特征之间的对应关系。

5 结论

泥石流冲击试验是探索泥石流冲击能量分布的一种有效途径。运用自行研制的试验模型，本文实施了A(粒径0.3 ～0.8 cm)、B(粒径0.8 ～1.5 cm)、C(粒径1.5 ～3.0 cm)三种固相粒径组，0.02，0.08，0.16，0.20和0.25五种固相比共计15种试验工况的水石流冲击试验，获取了85000多个测试数据。选用固相比为0.16的B组试验结果对水石流冲击信号能量分布进行了详细分析，初步结论如下:

(1)运用db8小波基变换对试验结果进行8层小波分解，得到了频率范围分别为0～0.195Hz，0.195～0.391Hz，0.391 ～ 0.781Hz，0.781 ～ 1.563Hz，1.563～3.125Hz，3.125 ～6.25Hz，6.25 ～ 12.5Hz，12.5 ～25Hz和25～50Hz共九个频率段泥石流冲击信号，获得了不同频段的冲击信号能量分布。

(2)水石流90%以上的冲击能量分布在小于0.195Hz的低频部分，中、高频段冲击能量分布仅占10%左右，水石流中粒径越小，中、高频段的冲击能量所占比例越小。

(3)中、低频段的水石流冲击能量总体呈现衰减分布趋势，但在频段三(0.391～0.781Hz)和频段六(3.125～6.25Hz)出现较显著的峰值，其中频段三的峰值强度略高于频段六，表明水石流也存在一定阵流现象。

(4)水石流中固相颗粒的粒径越小，低频段至高频段的冲击能量衰减速度越慢。

［1］Rickenmann D.Empirical relationships for debris flows［J］.Natural Hazards，1999，19:47 －77.

［2］Bagnold R A.Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear［J］.Proc.，Royal Soc.of london，1954，225:49 －63.

［3］Savage S B.Gravity flow of cohesionless granular materials in chutes and channels［J］.Journal of Fluid Mechanics，1979，92(1):53－96.

［4］Takahashi T.Debris flow on prismatic open channel［J］.Journal of the Hydraulics Division，Proceedings of the American Society of Civil Engineer，1980，106(HY3):381 －396.

［5］Arattano M，Savage W Z.Modeling debris flows as kinematic waves［J］. Bulletin ofEngineering Geology and the Environment，1994(49):3 －13.

［6］Iverson R M，Denlinger R P.Flow of variably fluidized granular masses across three-dimensional terrain:1.Coulomb mixture theory［J］.Journal of Geophysical Research，2001，106(B1):537－552.

［7］Valentino R，Barla G，Montrasio L.Experimental analysis and micromechanical modelling of dry granula flow and shocks in laboratory flume tests［J］.Rock Mechanics and Rock Engineering，2008，41(1):153 －177.

［8］Armento M C，Genevois R，Tecca P R.Comparison of numerical modelsoftwo debrisflows in the Cortina d’Ampezzo area，Dolomites，Italy［J］.Landslides，2008(5):143－150.

［9］费祥俊，舒安平.泥石流运动机理与灾害防治［M］.北京:清华大学出版社，2004.

［10］吴积善.云南蒋家沟泥石流观察研究［M］.北京:科学出版社，1990.

［11］魏 鸿.泥石流龙头对坝体冲击力的试验研究［J］.中国铁道科学，1996，17(3):50 －62.

［12］周必凡.粘性泥石流力学模型与运动方程及验证［J］.中国科学(B)，1995，25(2):196 －203.

［13］Chen N S，Yue Z Q，Cui P，et al.A rational method for estimating maximum discharge of a landslide-induced debris flow:a case study from southwestern China ［J］.Geomorphology，2007，84:44－58.

［14］张 宇，韦方强，王 青.基于动量守恒的粘性泥石流冲击力计算［J］.泥沙研究，2006(3):23－26.

［15］梁培金，张友谊.普斯罗沟泥石流运动特征和动力计算［J］.路基工程，2008(6):152 －153.

［16］巴仁基，王 丽，宋 志，等.泸定县牧场沟泥石流动力特性［J］.水文地质工程地质，2008(6):75－79.

［17］陈洪凯，唐红梅.泥石流两相冲击力及冲击时间计算方法［J］.中国公路学报，2006，19(3):19 －23.

［18］陈洪凯，唐红梅，陈野鹰.公路泥石流力学［M］.北京:科学出版社，2007.

［19］陈洪凯，唐红梅，鲜学福，等.泥石流冲击脉动荷载概率分布特征［J］.振动与冲击，2010，29(8):124 －127.

［20］孙云莲，刘敦敏.时频分析与小波变换及其应用［J］.武汉大学学报(工程科学版)，2003，36(2):103 －106.

［21］Arattano M，Savage W Z.Modeling debris flows as kinematic waves［J］. Bulletin ofEngineering Geology and the Environment，1994，4(9):3 － 13.

［22］陈洪凯，杜榕桓，唐红梅，等.泥石流龙头压胀机理探析［J］.重庆交通大学学报(自然科学版)，2008，27(5):790 －793.