基于EEMD的振动信号自适应降噪方法

陈仁祥，汤宝平，马婧华

(重庆大学 机械传动国家重点实验室，重庆 400030)

机械设备发生早期故障时，故障信号一般很弱，常常淹没在噪声信号中。因此，为了准确提取故障信息，需要对原始信号降噪，提高信噪比。由于机械设备振动信号的非高斯、非平稳特性，基于传统傅里叶变换的降噪方法存在保护信号边缘和抑制噪声之间的矛盾，难以正确识别信号中的噪声并加以去除。基于小波变换的降噪方法［1－2］，对非平稳信号降噪，要比传统的滤波降噪方法效果好，但这种方法存在选择小波基和确定阈值等问题［3－4］。

Huang等［5］提出一种新的非平稳信号处理方法——经验模式分解(Empirical Mode Decomposition，EMD)，EMD是一种完全基于数据驱动的自适应分解方法，能将信号从高频到低频分解成有限个具有物理意义的固有模式函数(Intrinsic Mode Function，IMF)和余项之和。文献［6］进一步分析了EMD方法对高斯白噪声的分解，得出EMD可以作为二进滤波器的结论。然而，EMD本身存在一些不足，如模式混叠、端点效应、停止条件等［7－8］。模式混叠是指1个IMF中包含差异极大的特征时间尺度，或者相近的特征时间尺度分布在不同的IMF中［10］，导致相邻的2个IMF波形混叠，相互影响，难以辨别。Huang［5］认为引起模式混叠的原因在于间歇现象(intermittency)，引起间歇现象的往往是异常事件(如间断信号，脉冲干扰和噪声等)。因此，模式混叠现象使EMD对含有异常事件的信号的降噪效果不佳［9－11］。

为了抑制模式混叠，Wu等［12］提出一种集合经验模式分解方法，该方法将噪声辅助分析应用于经验模式分解中，以促进抗混分解，有效的抑制了混叠现象。文献［11］将EEMD应用于对大型旋转机械启动过程中振动信号的降噪，得出了EEMD降噪既可以弥补小波降噪方法对调频调幅信号处理过程中存在的特征波匹配缺陷，又可以克服EMD降噪方法对脉冲干扰下振动信号滤波能力不足的结论。该文的方法是，对信号进行EEMD分解后计算IMF分量与原始信号互信息值来与事先确定的阈值对比以选取IMF分量重构信号，从而达到降噪的目的。但在该文中未明确说明阈值的确定方法。文献［13］将EEMD方法用于对疲劳应变信号降噪，其方法是对信号做EEMD分解后，选取IMF分量来重构信号以对疲劳信号降噪，但文中也未说明IMF分量的选取方法。

针对应用EEMD降噪时IMF分量选取问题，本文从白噪声经过EMD分解后的IMF分量特性出发，设计了自动选取IMF分量重构信号的算法，提出了基于EEMD的振动信号自适应降噪方法。

1 EEMD的基本原理及抗混分析

1.1 模式混叠产生分析

EMD方法自适应的将任意信号的分解成有限个IMF分量和余项之和，每个IMF需要满足两个条件［5］:① 在整个数据集中，极值点和过零点交替出现且极值点个数和过零点数相等或最多相差1个;② 在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成下包络线的平均值为零，即上、下包络线相对于时间轴局部对称。文献［5］中给出了EMD算法的详细步骤。

EMD过程中首先需要确定信号的局部极值点，然后用三次样条线将所有的局部极大值和极小值点分别连接起来形成上下包络线，再由上下包络线得到均值曲线。在求取包络线的过程中，当信号中存在异常事件时，势必影响极值点的选取，使极值点分布不均匀，从而导致求取的包络为异常事件的局部包络和真实信号包络的组合。经该包络计算出的均值，再筛选出的IMF分量就包含了信号的固有模式和异常事件或者包含了相邻特征时间尺度的固有模式，从而产生了模式混叠现象。

1.2 EEMD基本原理与方法

从前面的分析可知，极值点分布的不均匀导致了模式混叠现象。为此，Wu等［12］将白噪声加入待分解信号来平滑异常事件，利用白噪声频谱的均匀分布来使不同时间尺度的信号自动分布到合适的参考尺度上。同时，运用白噪声的零均值特性，经过多次平均使噪声相互抵消，从而抑制甚至完全消除噪声的影响。基于这种思想，文献［12］提出了集合经验模式分解。

显然，集合经验模式分解的本质是一种叠加高斯白噪声的多次经验模式分解。

EEMD的分解步骤如下:

第一步 在原始信号x(t)中M次(M＞1)加入均值为0，幅值标准差为常数的高斯白噪声ni(t)(i=1～M)，即:

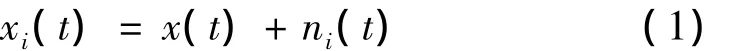
第二步 对xi(t)分别进行EMD分解，得到的K个IMF记为cij(t)(j=1～K)，余项记为ri(t)。其中，cij(t)表示第i次加入高斯白噪声后，分解所得到的第j个IMF。

第三步 利用不相关随机序列的统计均值为0的原理，将以上步骤对应的IMF进行总体平均运算，以消除多次加入高斯白噪声对真实IMF的影响，最终得到的EEMD分解后的IMF为:

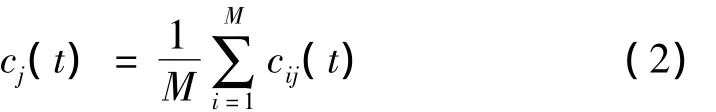
式中:cj(t)表示对原始信号进行EEMD分解后所得到的第 j个 IMF。

1.3 EMD与EEMD的比较

从EMD和EEMD的原理和算法可知，EEMD本质上是EMD的改进，它不仅具有EMD的优点而且可以有效抑制EMD分解过程中的模式混叠现象。下面通过仿真实例来说明EEMD抑制模式混叠的能力。

文献［5］提出了对于信号x(t)的正交性指标(Index of Orthogonality，IO)来评价EMD的精度，IO值越小则精度越高。IO可定义为［5］:

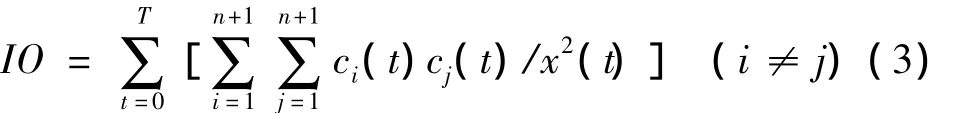
仿真信号s(图1(d))由Gauspuls脉冲分量干扰s1(图1(a))、频率为7Hz的正弦分量s2(图1(b))和趋势项s3(图1(c))组成，信号长度为1024点。

图2为仿真信号的EMD分解结果，包括三个IMF分量(c1～c3)和一个余项res。显然，只有c3和res才具有真实的物理意义，分别代表了原信号中的正弦成分和趋势项。c1完全失真，失去了物理意义，多出来的c2其实是s1和s2的模式混叠。事实上，c1和c2中都分布有s1和s2的特征时间尺度，所以，在这种情况下EMD无法分析信号本质，存在严重的模式混叠现象。图3为EEMD分解结果，加入高斯白噪声标准差为0.01，加入次数为100次。从图3中可以看出，c1代表了s1，c3代表了s2，res代表了 s3。多出来的c2时间尺度介于c1和c3之间，是由于s1和s2调制所致。

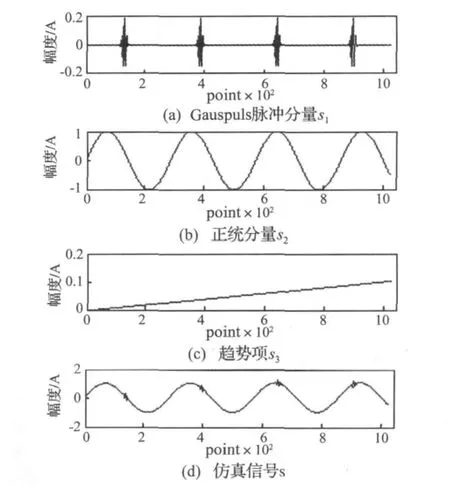
图1 仿真信号及其组成Fig.1 Simulation signal and its components

进一步比较EMD和EEMD方法计算效率和IO指标，如表1所示。显然EEMD的耗时比EMD多，但其IO值得到了很大提高。综上，EEMD有效地抑制了模式混叠现象，能高质量的分解出原信号中的各个组分，比EMD更具优势。

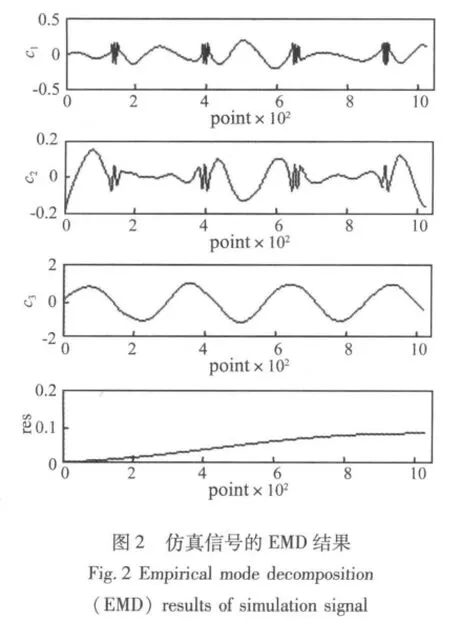
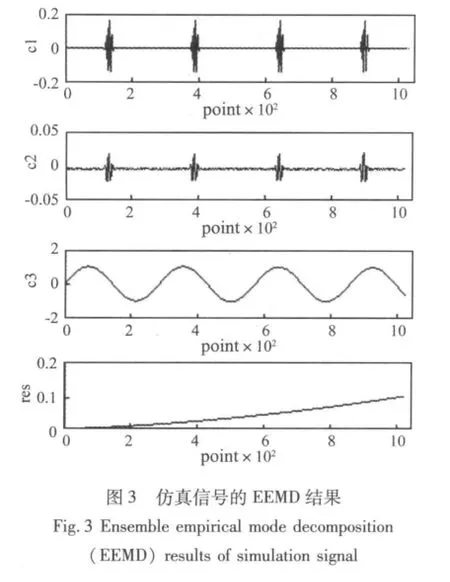
表1 两种分解方法结果比较Tab.1 A comparison between results of two decomposition methods

2 EEMD自适应降噪原理与方法

EEMD把信号分解成特征时间尺度由小到大即频率由高到底的一系列IMF分量。对混有随机噪声的信号，经分解后的高频IMF分量通常情况下为噪声，将这些噪声IMF分量去除，由剩下的IMF分量重构信号即可进行降噪。这就是EEMD降噪的原理。

在使用EEMD降噪时需要解决两个问题:① 应用EEMD分解信号时，需要设置两个参数，即加入原信号的白噪声的幅值系数k和执行EMD的总次数M;②重构信号时，选取IMF分量的方法。针对问题①，根据文献［12］，k用待分析信号的标准偏差乘以一个分数来定义比较合适，M取一、两百次时，残留噪声引起的误差为处在一个较低水平(小于1%)。经过笔者的试验分析，M 取100～300时，k值选择0.01～0.5倍信号的标准偏差较为适宜，M、k值可随噪声的强度而适当增大;针对问题②，由文献［14］的研究可知，白噪声序列经EMD滤波分解后各IMF分量的能量密度与其平均周期的乘积为一常量，从该性质出发，设计了一种自动选择IMF分量的方法。具体步骤是:

第一步对含噪信号进行EEMD分解后得到K个IMF分量，计算出每个IMF分量的能量密度与其平均周期之积:

式中:Ej和为第j个IMF分量的能量密度和平均周期，其计算公式如式(5)和式(6):

式中:N为每个IMF的长度，Aj为第j个IMF分量的振幅，Oj为第j个IMF分量的极值点总数。

第二步根据式(7)计算系数RPj(j≥2)

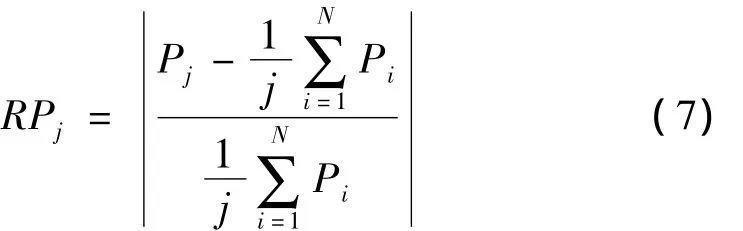
当RPj≥1时，可确定第j个IMF的Pj相对于前面j－1个IMF的Pj的平均值成倍增大，即认为前面j－1个IMF的能量密度与其平均周期之积为一常量。由上文可知，前面的j－1个IMF分量作为噪声而去除，同时，余项作为趋势项也应去除，由剩下的IMF分量重构信号即可对原含噪信号进行降噪。

综上，该降噪方法计算流程如图4所示。

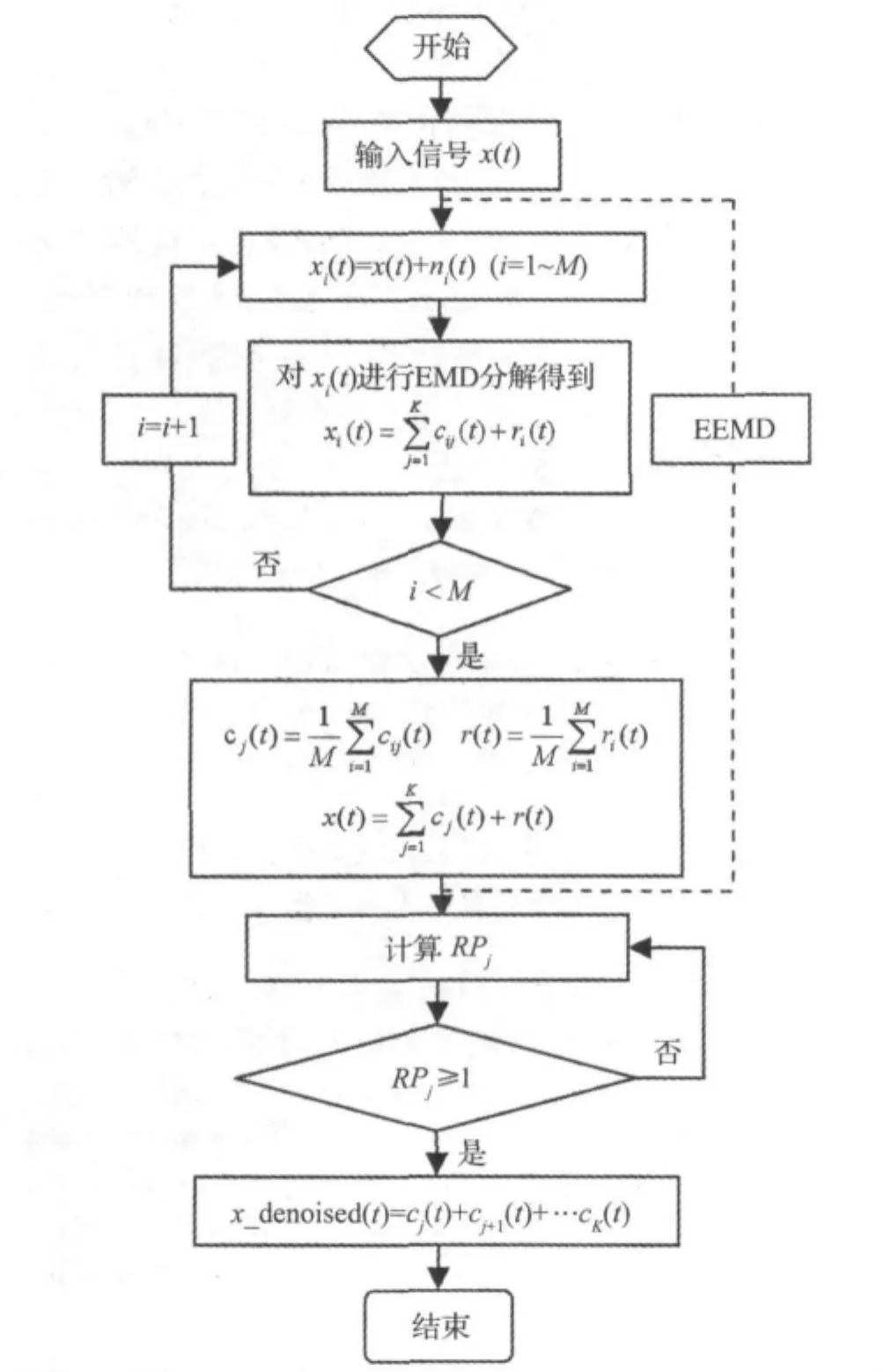
图4 降噪算法流程图Fig.4 Flow chart of de-noising method

3 仿真试验分析

仿真信号s_noise由前文中的仿真信号s加上标准差为0.4的白噪声组成，信号长度为1024点，波形图如图5所示。

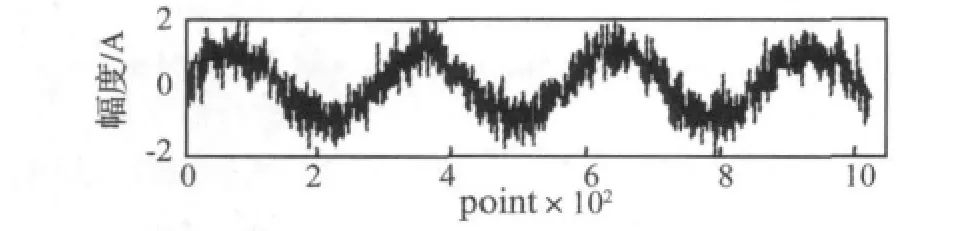
图5 仿真信号s_noiseFig.5 Simulation signal s_noise

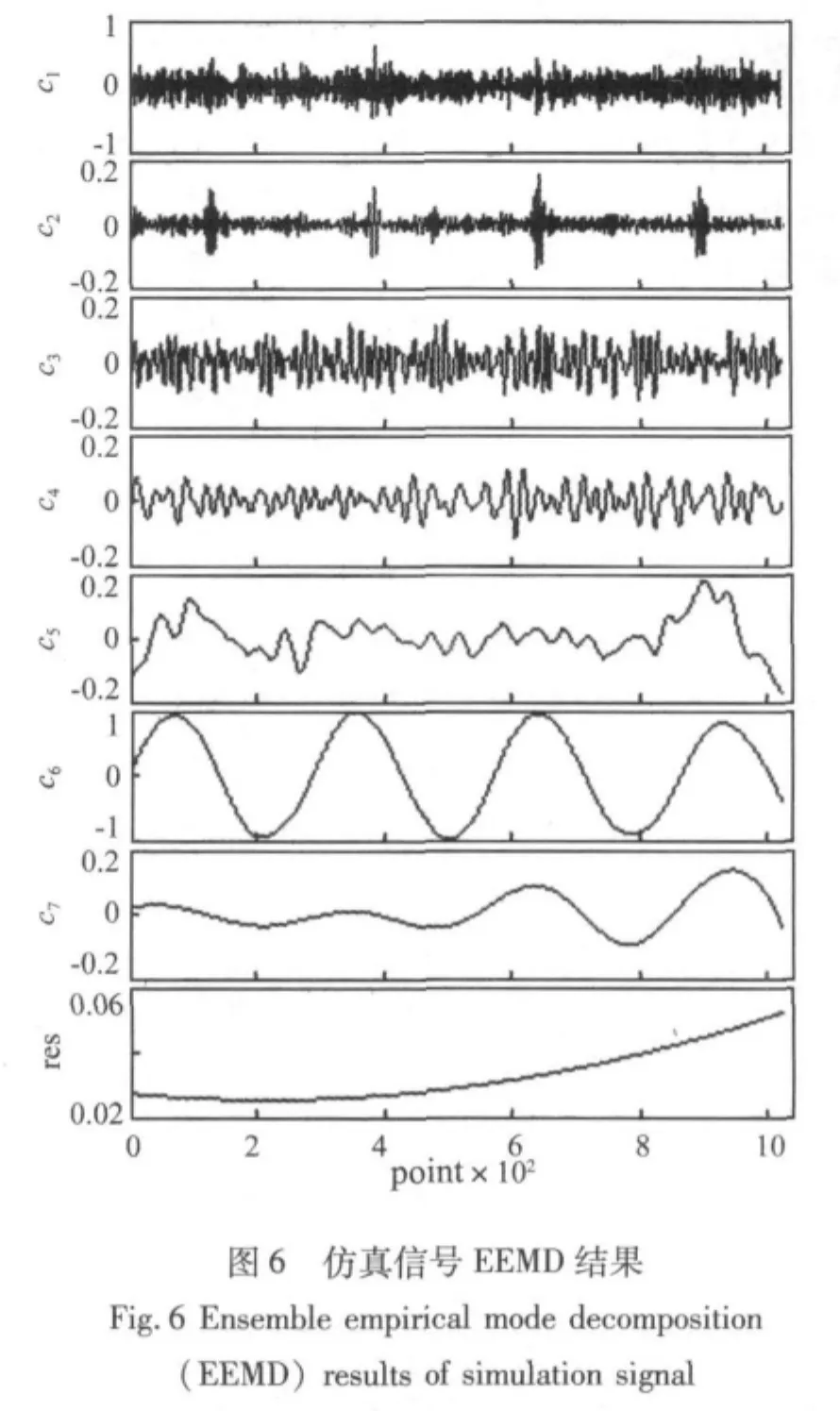
首先对 s_noise进行 EEMD分解，M=100，k=0.02，结果如图6所示，一共分解出7个IMF分量和一个余项。根据本文提出的降噪算法流程，计算其RP值得出当j=6时，RP=5.7401＞1，所以自动选取c6和c7重构信号，降噪结果如图7(b)所示。图7(a)为EMD降噪结果，圆圈处出现明显的扰动成分，这是由于EMD的模式混叠所引起。

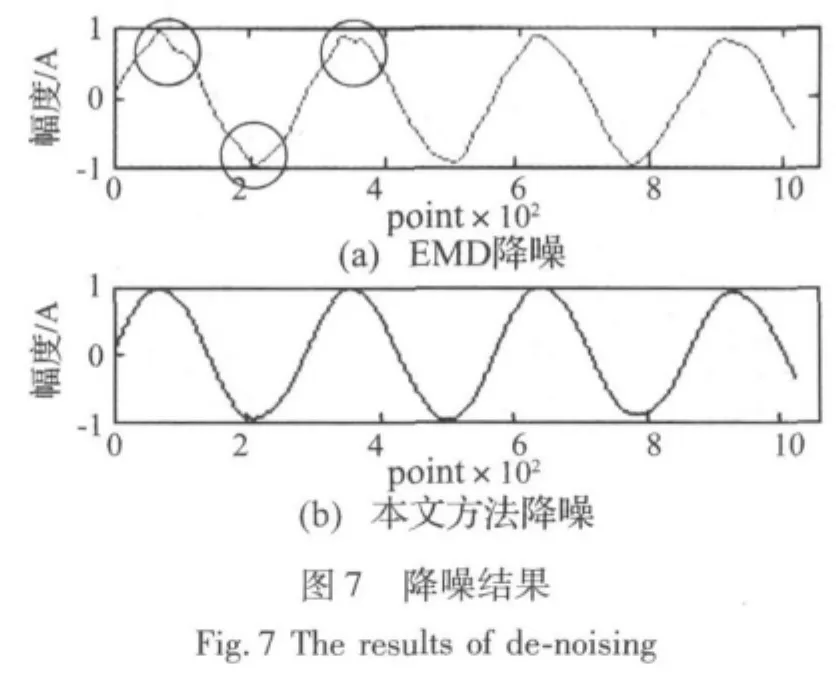
根据式(8)计算出信噪比，结果如表2所示。

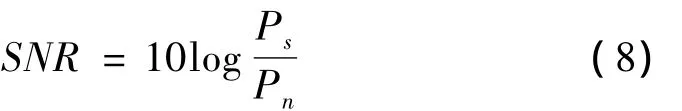
式中:Ps和Pn分别是信号和噪声的有效功率。

从表2中可以看出，经过降噪处理后，信号的信噪比得到了大幅度提高。同时，本文方法降噪后的信噪比更高，证明了本文提出的降噪方法是可行的，且更为有效。

表2 两种降噪方法信噪比Tab.2 The SNR of two de-noising methods

4 工程应用

将本文提出的降噪方法应用于轴承振动数据的降噪。试验台由电动机、轴承、转子、传动轴、轴承支架、模拟载荷、电器控制装置等组成，以输入端轴承为测试对象。采集部分选用16位的信号采集仪和压电加速度传感器套装，传感器布置在轴承座的垂直方向。现场试验图如图8所示。

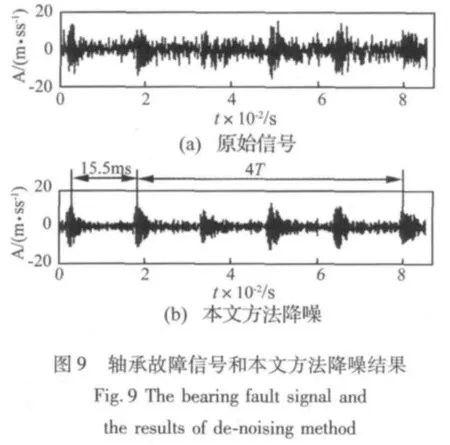
轴承型号为UN205，其内径为25mm，外径为52mm，滚动体直径为7.5mm，滚动体数目为12，接触角为0°。该轴承外圈存在故障，转速为800 r/min，经过计算其外圈故障频率为64.4Hz。原始数据长度为1024点，采样频率为12 k，其波形如图9(a)所示。受噪声干扰影响，从图9(a)的时域波形中观察故障特征较困难。

图9(b)为采用本文提出的降噪方法的结果，从图中可以明显看出冲击的周期性，并且周期性脉冲衰减明显。其冲击周期T约为15.5 ms，其倒数即是信号特征频率为64.5Hz，该频率和前文计算出的轴承外圈故障特征频率吻合，由此可判断轴承出现了外圈故障，与实际相符。

5 结论

EEMD能有效的抑制EMD中的模式混叠现象，其分解精度也更高。在应用EEMD降噪时，给出了EEMD中参数选取原则，并根据白噪声经EMD分解后其IMF的特性，设计了一种自动选取IMF分量重构信号的算法，提出了基于EEMD的振动信号自适应降噪方法。通过应用本文方法对仿真信号和轴承振动降噪，验证了该方法的可行性和有效性，为机械振动信号降噪提供了一种新方法。

［1］Liu F，Ruan X E.Wavelet-based diffusion approaches for signal de-noising［J］.Signal Processing，2007，87:1138－1146.

［2］Azzalini A，Farge M，Schneider K.Nonlinearwavelet thresholding:A recursive method to determine the optimal denoising threshold［J］.App.l Comput.Harmon.Ana，l 2005，18:177－185.

［3］张吉先，钟秋海，戴亚平.小波门限消噪法应用中分解层数及阈值的确定［J］.中国电机工程学报，2004，2(24):118－122.

［4］程发斌，汤宝平，钟佑明.基于最有Morlet小波和SVD的滤波消噪方法及故障诊断的应用［J］.振动与冲击，2008，27(2):91－94.

［5］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences，1998，454:903－995.

［6］Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter bank［J］.IEEE Signal Processing Lett，11，2004:112 －114.

［7］Rilling G，Flandrin P，Goncalyes P.On empirical mode decomposition and its algorithms［C］//IEEE-EURASIP Workshop on Nonlinear Signaland Image Processing(NSIPL2003)，Grado(1)，June，2003:8 －11.

［8］Rato R T，Ortigueira M D，Batista A G.On the HHT，its problems，and some solutions［J］.Mechanical Systems and Signal Processing，2008，22:1374 －1394.

［9］Norden E，Huang N E.A new view of non-linearwaves:The Hi-lbert spectrum［J］.Annual Review of Fluid Mechanics，1999，31:417－457.

［10］赵进平.异常事件对EMD方法的影响及其解决方法研究［J］.青岛海洋大学学报，2001，31(6):805－814.

［11］曹冲锋，杨世锡，杨将新.大型旋转机械非平稳振动信号的EEMD 降噪方法［J］.振动与冲击，2009，28(9):33－38.

［12］WuZH， HuangN E. Ensembleempiricalmode decomposition:a noise assisted data analysis method［J］.Advances in Adaptive Data Analysis，2009，1(1):1 －41.

［13］陈 隽，李 想.运用总体经验模式分解的疲劳信号降噪方法［J］.振动、测试与诊断，2011，31(1):15－19.

［14］Wu Z，Huang N E.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proc.R.Soc.London A，2004，460:1597 －1611.