非光滑凸半无限规划的最优性条件

戴素芬

(重庆师范大学，重庆 401331)

若R是有效域，一般的半无限规划(SIP)有如下形式［1－7］:

其中:x∈R;T是一个无限集。

出于此目的，文献［8］中，Pshenichny将(P)换为:的最优性条件涉及到f(x)的次微分，但f是非光滑的。

一般来说，尽管函数ft(x)(t∈T)是凸函数且可微，且的直接转换。应当指出的是，当(P)退化到一个有限规划后，利用有限最优性理论，可以给出最优性条件。

文献［1］中，Ben-Tel，Kerzner和Zlobecgec给出了解凸SIP的不同方法，得到一个与原问题有相同最优值的有有限约束的子问题他的特定方法基于水平集的凸性假设，哪怕将他的结论推广到那些所涉及的函数是拟凸函数的问题和那些插入到子问题的约束中的函数是严格拟凸的问题也同样适用。只有在的所有函数(包括目标函数)都是凸函数且(P)的最优值v(P)有限时才能得到一个拉格朗日条件。

本文最优性条件对于涉及标准拉格朗日鞍点概念的凸SIP是存在的，局部和全局的约束品性是给定的，对于特定线性化系统，它们展现了其超越F-M性质的优越性。

这篇文章结构如下:第1部分引入了一些符号和初步结果;第2部分包含了对于非光滑凸SIP的拉格朗日鞍点的特征，给定2个约束品性:一个局部的，称为拉格朗日准则，另一个是Slater品性的推广，论证了Slater品性蕴含了所有可行点的拉格朗日准则;第3部分介绍了一个全局约束品性，它蕴含在Slater品性中，通过函数ft的次梯度给出可行集S的一个线性表示。函数ft的次梯度在S的某些边界点上函数值为0。

将一个凸SIP的线性表示与F-M性质的重要性联系起来，可得出结论:Slater品性对于SIP太过严格。本文第3部分及文献［3］中的定理3.2证明了Slater品性产生典型地闭线性系统，且F-M性质更为广泛，这些思想涉及到不同的可能性，如试图将(P)的拓扑性质利用到它在T上的独立性。沿着这些方向，也可能会涉及到文献［1］中的一致中值性质。

1 符号和初步结果

令ft，t∈{}T是R中由有限凸函数构成的集合，子标集T是无限集，在R中考虑凸不等式系统:{ft(x)≤0，t∈T}。

记S为该系统的解集，当S≠∅时，系统是相容的。当2个系统有相等的解时称它们是等价的。定义集合分量λt中只有有限个不为0，其余都为0}。

给定一个非空集C⊂R，记〈C〉为C的凸包，K(C)为由C生成的凸锥，clC为C的闭，intC为C的内部，C*为C的对偶锥，R中的零向量记为0n。

令 {a'tx≤βt，t∈T}是R中的一个线性无限系统，若该系统的每一个解都满足关系a'x≤β，则称a'x≤β是该系统的一个后承关系。

现介绍要用到的已知结论。

引理1(文献［5］中的引理 14.1)a'x≤0是系统 {a'tx≤0，t∈T}的一个后承关系，当且仅当a∈clK{ at，t∈T}。

引理2(文献［5］中的引理 14.2)a'x≤β 是相容系统 {a'tx≤βt，t∈T}的一个后承关系，当且仅当a'x+βτ≤0 是系统 {a'tx+βτ≤0，τ≤0，t∈T}的一个后承关系。

定理1 a'x≤β 是相容系统 {a'tx≤βt，t∈T}的一个后承关系，当且仅当

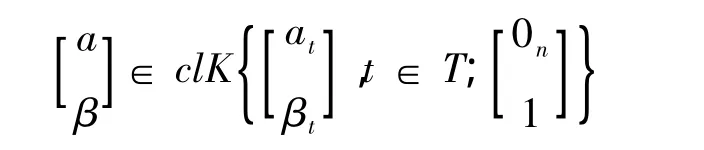
证明由引理2知，a'x≤β是系统 {a'tx≤βt，t∈T}的一个后承关系，当且仅当a'x+βτ≤0是系统{a'tx+ βτ≤0，τ≤0，t∈T}的一个后承关系，即蕴含再由引理1知最终结论可由引理1得到。

定义1 对于相容系统 {a'tx≤βt，t∈T}，若它的每一个后承关系都是一个有限子规划的后承关系，则该相容系统满足Farkas-Minkowski性质(F-M性质)。

定义2 系统 {a'tx≤βt，t∈T}是典型闭(CC)的，若满足:

① 存在一个代数内点，即∃x0∈Rn，对于所有的 t∈T，有

定理2［6］相容系统满足F-M性质，当且仅当是闭集。

F-M性质保证了对应的系统产生一致LP对偶性。

推论1［6］系统满足F-M性质，当且仅当是闭集。

推论2［10］若相容系统满足以下条件之一，则它是一个F-M系统:

②系统是典型闭的。

在文献［6］中由定理2.6直接推导出证明过程。条件②由文献［4］中Duffin和Karloviz证明。

2 与拉格朗日鞍点有关的最优性条件

将拉格朗日函数与问题(P)联系起来:

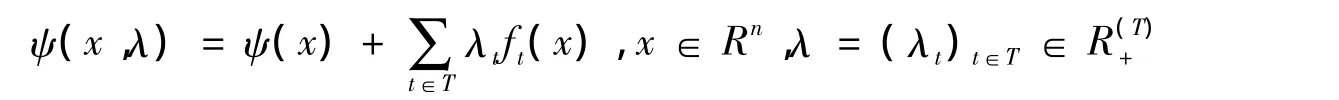
以下命题刻画了涉及给定的鞍点的存在性。

引理3 给定，存在一个与有关的拉格朗日鞍点，当且仅当∃x∈S，且

证明假设是一个拉格朗日鞍点，由于是(P)的一个最优解。此外是凸函数的一个全局最小，则

而

是一个闭凸锥，可证:

引理4 若，则。

证明对于，则对，若则

定义3 点称为一个拉格朗日正则点，若:

条件②是Guignard品性到非光滑半无限情形的推广。条件③是系统在处存在F-M性质的充分必要条件。由于T是有限的，且为可微函数是一个多面体锥，所以条件③成立。

以下给出一个必要最优性条件。

引理5 令是凸SIP的一个最优解，若x是一个拉格朗日正则点，则存在是 ψ的一个鞍点。

在对凸SIP的Slater品性作出推广之前，分析一个凸函数的水平集的代数内部和拓扑内部之间的关系。

引理6 令f(x)是R中的一个凸函数，且，则S0≠∅蕴含着intS=S0。

证明由连续性S0⊂intS。给定y∈intS且x0∈S0。当y≠x0时，取z∈S，s.t.y介于x0与z之间的内部，由于f(x0)＜0且f(z)≤0，由连续性有f(y)＜0。

注:当f(x)是一个下半连续的严格拟凸函数时，以上结论仍然成立。

定义4 凸SIP的Slater品性:

①T⊂R是一个紧集;

② ft(x)是T×R中(t，x)的一个连续函数;

③ 存在一个点x0，使得对于所有的t∈t，ft(x0)＜0。

对于满足条件①的凸SIP，利用文献［9］中的定理10.7，条件② 可改为:对于每一个x∈R，f(·，x)是t处的连续函数。

对于定理3，需要一个初步引理，该引理是Gordon择一性定理的一个推广。

引理7对所有t∈T，令at∈R，若〈at，t∈{}T〉是一个闭集，则以下命题(Ⅰ)和命题(Ⅱ)有且仅有一个成立。

命题(Ⅰ):{a'tx＜0，t∈T}是相容的。

命题(Ⅱ):0n∈〈at，t∈{}T〉。

证明若∃t∈T，at=0，则结论成立。

假设对所有的t∈T，at≠0n。首先，证明命题(Ⅱ)成立时 命题(Ⅰ)不成立。

采用反证法，假设命题(Ⅰ)成立，x是命题(Ⅰ)的一个解，则对。因为命题(Ⅱ)成立，所以，因此0，矛盾，即命题(Ⅱ)成立时命题(Ⅰ)不成立。

现证命题(Ⅰ)不成立时命题(Ⅱ)成立。

采用反证法，假设命题(Ⅱ)不成立，即0∉〈{at:t∈T}〉。由严格凸集分离定理可知，∃c∈R，c≠0，s.t.c'at＜0(∀t∈T)，所以c为命题(Ⅰ)线性系统的解，矛盾，即命题(Ⅰ)不成立时命题(Ⅱ)成立。

现依然假设〈{at，t∈T}〉是闭集。

定理3 假设凸SIP满足Slater品性，所有可行点都是拉格朗日正则点。

证明令，对所有 t∈T}，定义

3 全局约束品性:F-M线性化

对于凸SIP，给定一个全局约束品性，在每一个最优解x处与本文第2部分要求的拉格朗日正则点的局部条件交错开来以得到必要最优性条件。事实上，Slater品性涉及了所有约束构成的集合且该部分涉及的品性也蕴含其中。

定义5 将非光滑凸SIP与以下线性不等式系统结合起来:

由凸性知，ft(y)≥ft(x)+▽ft(y)T(y－x)，即 ft(y)≥ft(x)+u'(y－x)，由于 ft(y)≤u'(y－x)，所以ft(x)≥0，即系统(1)的解集即为凸SIP的可行域S，因此，以上系统是凸SIP约束的一个线性表示。

定义6(F-M品性)凸SIP的约束满足F-M品性，若与系统(1)等价的系统是一个F-M系统。

定理4 若是满足F-M品性的一个凸SIP的一个最优点，则是一个拉格朗日鞍点。

证明由于是问题mx∈inSψ(x)上的一个最优解，所以对所有 x∈S，有

当 t=ti，令且若 t≠ti，令，则是ψ的一个鞍点。

在证明主要结论，即定理5(它给出了Slater品性与F-M品性之间的关系)的过程中，需要一个初步引理，其中用Sb表示S的边界。

引理8 令S⊂R是一个闭凸集，{ct'x≤δt，t∈T}是满足以下条件的一个系统:

①S的每一个点都是该系统的解;

② ∃x0∈S，s.t.ct'x0＜ δt，t∈T;

③ 给定∀y∈Sb，∃t∈T，s.t.c'ty= δt。

现阐述该部分的主要结果，其中给出Slater品性的有限性质，从这一结论中得到F-M性质的重要性。

定理5 若凸SIP满足Slater品性，且S有界，则该凸SIP满足F-M品性。

证明回忆，且，系统为

该系统构造S的一个线性表出，可以看出引理8的假设成立:

①S的每一个点都是系统(2)的一个解;

②x0是系统(2)的一个代数内点;

③给定y∈Sb，存在满足等式的系统系统(2)的关系。

应证系统(2)是典型闭，从而系统(2)是F-M系统。令集合

需证A是紧集。

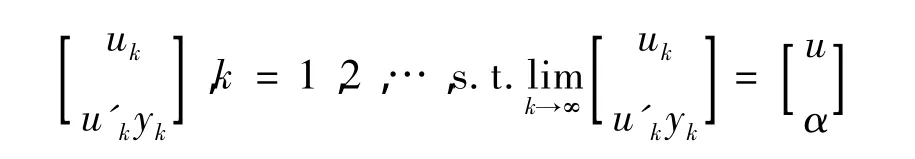
另一方面，知道∂f在R×R上的图像是一个闭集，因此u∈∂f(y)［9］233。

以下可得A是闭集。由Schwarz不等式知A是有界的，取和，向量 A的范数以为上界。

若只有解集S的线性化 {a'px≤βp，p∈P}要求满足F-M性质，定理4同样适用，它证实了以下性质:

对每一个 p∈P，∃tp∈T，s.t.对于所有

任何这样的线性系统都构造了文献［7］中介绍的一个特定例子，一般来说，系统(1)和(2)结合凸SIP，证实了性质(3)。

根据这一可能的准则，F-M品性非常弱，几乎给出在一个最优点产生一个鞍点的充分必要条件，不管目标函数是什么，在这种想法的驱使下，若约束的原始系统展现了一致凸对偶性，得出结论:将一个线性正则变形(它可以产生一个F-M系统)与约束的初始系统联系起来是有可能的。

［1］Ben-Tal A，Kerzner L ，Zlobec S.Optimality conditions for convex semi-infinite programming problems［J］.Naval Research Logistics Quarterly，1980，27:413 －435.

［2］Ben-Tal A，Rosinger E E，Ben-Israel A.A Helly-type theorem and semi-infinite programming［M］//Coffman C V，Fix，eds G J.Constructive approaches to mathematical models.New York:Academic Press，1979:127 －135.

［3］Borwein J M.Direct theorems in semi-infinite convex programming［J］.Mathematical Programming，1981，21:301 －318.

［4］Duffin R J，Karlovitz L A.An infinite linear program with a duality gap［J］.Management Science，1965，12:122 －134.

［5］Eremin I I，Astafiev N N.An introduction to the theory of linear and convex programming［M］.Moscow:［s.n.］，1976.

［6］Goberna M A，Lopez M A，Pastor J.Farkas-Minkowski systems in semi-infinite programming［J］.Applied Mathematics and Optimization，1981，7:295 －308.

［7］Jeroslow R G.Uniform duality in semi-infinite convex optimization［J］.Mathematical Programming，1983，27.

［8］Pshenichnyi B N.Necessary conditions for an extremum［M］.New York:Dekker，1971.

［9］Rockafellar R T.Convex analysis［M］.Princeton，NJ:Princeton University Press，1970.

［10］Lopez M A，Vercher E.Optinality conditions for nondifferentiable convex semi-infinite programming［J］.Mathwmatial Programming，1983，27:307 －319.