基于Markov过程的逆向物流回收量预测

陈义华，许庆春

(重庆大学 数学与统计学院，重庆 400044)

近年来，随着市场竞争的日益激烈以及国家对环境保护的法律强制要求，国内外许多企业开始把有效管理顾客退货和废旧产品回收作为一种新的竞争方式和降低成本的有效途径。学者们把这种物品逆向流动的供应链称之为逆向供应链，以与传统正向供应链相区别。与正向供应链相比，逆向供应链具有系统高度复杂性、系统目标多样性、系统供需失衡性、系统汇聚性等4个特点。回收产品在回收时间、回收质量和数量等方面具有很大的不确定性［1］，而对这种不确定性进行预测的方法的合理性和精确性，直接关系到产品回收设施能力的规划和产品再制造库存管理的优化与控制，因此如何及时、准确地进行产品回收预测成为实施逆向物流的重要前提。影响产品回收量的主要因素有产品的相对生命周期、产品的回收途径、产品的销售量、消费者的购买行为等。在过去的研究中，学者们在对产品回收预测的研究中主要是假设产品的需求和返回服从独立的泊松分布或者正态分布［2－3］。谢家平等［4］运用随机网络的相关理论构建了以生产厂商为回收主导的废旧电器产品回收随机网络预测模型。此外还有学者［5－6］对灰色系统模型进行了改进，并把模型应用到了回收量的预测中。

Markov链建模具有很强的实用性，可以被用于诸多研究领域来解决状态转移问题［7］，包括用于回收产品的库存管理［8］。于洋等［9］应用灰色Markov链改进预测方法，对铁路集装箱中心站货运量的发展趋势进行了预测。谢家平［10］通过对逆向回收产品的不同状态的界定，剖析其状态转移过程，然后根据Markov链的原理，构建了一个不同状态下的转移方程，在给定的初始状态下，预测某一时期期末所处不同状态的回收产品数量。本文在文献［10］的基础上考虑回收的产品经处理后会有2种状态:一是转换成全新的产品;二是有一定的废弃率，并根据以上考虑建立了预测模型。

1 Markov链

事物的未来发展及演变状态仅仅受事物现在状态的影响，而与过去的状态无关，则称该事物具有Markov性(也称无后效性)。有限个Markov过程的整体称为Markov链。所谓Markov链是一类时间为参数离散，状态空间为可列集或有限集，且具有Markov性的随机过程［11］，它可用数学语言表述为:在概率空间(Ω，F，P)上的随机序列{X(t)，t∈T}，其中参数集 T={0，1，2，3…}，状态空间 E={0，1，2，3…}。若 X(n)=i就说过程在时刻n处于状态i。假设每当过程处于状态i，则在下一时刻将处于状态j的概率pij是固定的，即过程在下一时刻的状态仅与当前的状态有关，而与以前的状态无关，这一过程称为Markov过程，其中pij为一步转移概率。Markov过程按其状态和时间参数是连续的或离散的可以划分为3类:

1)时间和状态都是离散的Markov过程，也称为Markov链。

2)时间连续、状态离散的Markov过程，也称纯不连续的Markov过程。

3)时间和状态都是连续的Markov过程。

本文所利用的Markov过程属于第1种情况。由于逆向物流的特征很好地符合了Markov随机过程，因此逆向物流的过程是一个比较理想的Markov过程，可以用Markov过程的相关理论对逆向物流系统的回收量进行预测。在利用Markov过程进行回收量预测时最关键的是确定产品的状态转移概率，一般可从企业长期收集的产品回收数据中总结提炼出产品各状态间的转移概率。转移概率与产品的工艺和质量密切相关，这种概率在长期内是稳定的，所以这种方法比较适用于技术成熟的产品的回收预测。在已知状态转移概率后即可对回收量进行预测。

2 废弃产品回收量预测

本文研究单一产品的回收量预测问题。假设产品的生命周期等分为4个阶段，每阶段时间长度为t，在同一时间处于各个状态的产品市场上都有，厂商每隔时间t会对市场上需要回收的产品进行回收，不需要回收的产品直接进入生命周期的下一阶段，回收的产品经维修后会有一定的废弃率和一定的维修率，且维修后产品与新产品无异，在下一阶段会以全新产品的形式进入市场。产品的状态间存在如图1所示的转换关系。

图1 产品的状态转换Markov链示意图

图1中 si(i=1，…，5)为产品不同的状态，其中s1为全新状态，s5为废弃状态，即不可再利用的状态。处在状态s1的产品经过时间t后需要回收的概率为1－p1，其中可修复的概率为p5，废弃的概率为1－p1－p5，其余产品状态经过时间t后转换概率如图1所示。当产品处在状态s5时，表示产品已经报废不可再利用。状态s5到达了吸收态，也就是产品一旦到达该状态便被“吸住”不再转移。所以对图1所示的产品状态的转移概率矩阵可表示为

用pij表示矩阵P的第i行第j列的元素，则pij表示产品由状态si经过时间t后转移到sj的概率，且

2.1 回收预测条件假设

1)厂商生产的产品有一定的使用寿命。

2)每隔时间t记为一期，厂商在每一期期末对市场上需要回收的产品进行回收，回收再制造后的产品与新产品无异，即产品进入状态s1，且在下一期进入市场。

3)每一期始点处市场需要的产品数量已知，且全部被满足。若在上一期期末回收的产品满足不了市场的需求，厂商将投放一批新生产的产品;若上一期期末回收的产品大于市场的需求量，厂商可以自行决定对多余的再制造产品的处理方法。

2.2 废弃产品回收量预测

假设企业首次使用本模型时市场中处于各种状态的产品数量用行向量表示为，在第 k(k=1，2，…)期期初市场的需求量为qk，在第k(k=1，2，…)期期末经企业回收后修复成全新产品的数量为，则在第k(k=1，2，…)期期初企业需要生产的新产品数量为若，则企业需要投放一批新产品;若，则说明企业在上一期期末经回收后再制造的产品数量大于市场的实际需求量。=(，0，0，0，0)第 1 个数字是的一维行向量。有了上述符号的定义及状态转移概率矩阵可得产品的状态转移方程:

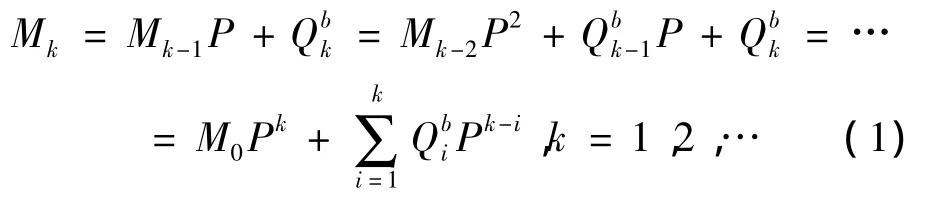
由式(2)可得第k期需要回收的产品数量为

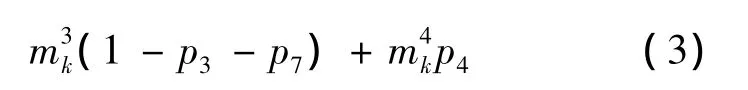
其中报废的数量为

将式(5)代入式(1)得到第k期时市场上各种状态的产品数量的行向量

由式(3)～(5)即可得到企业在每一期需要回收的产品数量、报废的产品数量和需要生产的新产品数量。

3 实例分析

假设企业在进行预测的期初市场中处于各种状态的产品数量为 (2 000，4 500，5 000，6 000，0)，状态转移概率分别为(0.90，0.75，0.60，0.80，0.05，0.15，0.25)，市场在每一期开始时需要的产品数量分别为 2 000、4 500、5 500、5 000、4 500、4 200。根据这些数据，可以预测在第5期期末企业需要回收的产品数量、报废的产品数量和第6期是否需要生产全新产品及其生产量。首先根据给出的状态转移概率可得产品的状态转移概率矩阵

把数据带入式(6)，使用Matlab编程计算得到在第5期市场中各种状态的产品数量为:(4 500，4 500，3 712.5，1 822.5，16 023.38)，所以由式(3)得第5期需要回收的数量为 4 882.5，由式(4)得报废的数量为2 689.88，由式(5)得第6期需要生产的数量为2 007.38。

4 结束语

逆向物流中产品回收数量的不确定性对产品的生产计划、库存管理与回收网络的建立都有重要的影响。本文应用Markov链把产品的状态数量和时间的预测有机地结合在一起，实现了对逆向物流回收量的预测。

［1］Thierry M，Salomon，van Nunen J A，et al.Strategic Issues in Product Recovery Management［J］.California Management Review，1995，37(2):114 －135.

［2］Toktay L B，Wein L M，Zenios S A.Inventory Management of Remanufacturable Products［J］.Management Science，2000，46(11):1412 －1426.

［3］Bayindiret Z，Nesim Erkip，Refik G.A Model to Evaluate Inventory Cost in a Remanufacturing Environment［J］.International Journal of Production Economics，2003，81/82:597－ 607.

［4］谢家平，吉少华.基于随机网络的废弃产品回收预测模型［J］.当代经济管理，2008(2):40－43.

［5］赵鹏，雷涛.基于灰色系统理论的汽车报废量预测［J］.工业技术经济，2011(4):31 －35.

［6］刘文杰 ，方志耕.IGM(1，1)－TNF模型在产品回收预测的应用［J］.控制理论与应用，2007(3):459－464.

［7］White D J.A Survey of Applications of Markov Decision Processes［J］.The Journal of the Operational Research Society，1993，44(11):1073 － 1096.

［8］Chinget W K.An Inventory Model with Returns and Lateral Transshipments［J］.Journal of the Operational Research Society，2003，54:636 － 641.

［9］于洋，杨学斌.基于灰色马尔可夫链改进方法的预测方法［J］.统计与决策，2008(13):53 －55.

［10］谢家平，葛夫财.基于Markov链的逆向物流回流预测［J］.科技进步与对策，2007(10):37 －40.

［11］刘金甫，孙洪祥，王军.应用随机过程［M］.北京:清华大学出版社，2006.

［11］陈冬梅，邱屹峰，逄兆勇.基于逆向物流的城市固体废弃物回收［J］.重庆工商大学学报:自然科学版，2008(4):398－402.