基于多层线性模型的GDP影响因素分析
李春红,韦泽多,卢玉桂
(广西大学数学与信息科学学院,南宁 530004)
随着科技的进步和社会的发展,科技对GDP的贡献越来越大。科技投入与经济增长的关系一直是科技界、经济学界广为关注的问题之一。国内不少学者从不同角度对科技投入与经济增长进行了研究。文献[1]利用简单线性回归方法,研究科技投入与GDP能耗之间的关系。文献[2]从自回归角度研究科技投入对GDP的拉动效应。由于区域因素的影响,各个省份的科技力量有所不同,其对经济发展的影响有很大的差异,因此根据我国总体情况得出的结论并不适用于各个省份。本文利用多层线性模型,分析我国31个省份2003—2008年经济增长趋势,揭示各省科研经费利用率、科技人员比例等基本科技力量和经济发展的互动关系。多层模型能够同时分析各个层次上的数据,估计数据在各层次上的变异,并能通过已知变量预测各层次上的变异值,因此比传统模型更有优势[3-5]。
1 多层线性模型
1.1 模型介绍
多层模型的基本原理:将因变量中的变异分解为2部分,即同一群体内的个体差异和不同群体之间的个体差异。该模型克服了传统统计方法以单一形式表示残差和忽视个体内在相关性的缺点,提供了残差在个体以及各层次上的信息,将个体的组群效应考虑在内,从而可得到更加准确的结果。常见的多层线性模型是2层结构的模型,一般形式为:
层1(个体)
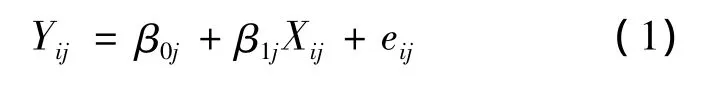
层2(群体)

合并模型可以表示为

其中:Yij为研究对象j的第 i次的结局变量;β0j为截距,其含义是第j个观测对象的平均数;β1j是回归斜率,其含义是第j个观测对象的变化速率;eij是误差项(假设其服从正态分布eij:N(0,σ2)),其含义是第i个观测对象在第j个观测时间中的测量值Y不能被自变量X所解释的部分。方程(1)与一般的回归方程很相似,区别在于它的截距和斜率不是常数,而是随机变量,不同观测对象具有不同的截距和斜率,它们可能受到第2层变量的影响。
γ00是方程(2)的截距,可以被理解为自变量Wj为0时观测对象在因变量Y上的平均数。如果该系数的统计检验显著,意味着因变量的初始值不等于0。通常纵向研究中的研究者并不关心这一系数。
γ01是方程(2)中自变量Wj的回归系数,可以被理解为自变量Wj对方程(1)中因变量Y初始值的影响大小。追踪研究中,如果对该系数的统计检验达到显著,意味着不同自变量水平的观测对象在观测起点上的初始值有显著差异。
u0j是方程(2)中的残差,可以被理解为方程(1)中因变量Y初始值未被自变量Wj所解释的部分。如果对相应方差的统计检验达到显著,意味着模型中需要引入新的变量来解释因变量初始值上的变异。
γ10是方程(3)的截距,可以被理解为自变量Wj为0时观测对象的变化速率。在纵向研究中通常把它看作基础变化速率。如果对该系数的统计检验达到显著水平,则认为基础变化速率不等于0。
γ11是方程(3)中自变量Wj的回归系数,可以被理解为自变量Wj对观测对象变化速率的影响大小。这一系数是纵向研究中最受关心的结果,可用于探索哪些因素能解释不同个体在变化速率上的差异。如果对该系数的统计检验达到显著性水平,意味着自变量Wj是导致个体变化速率差异的重要原因。
u11是方程(3)中的残差,可以被理解为方程(1)中因变量Y变化速率未被自变量Wj所解释的部分。如果相应方差的统计检验达到显著,意味着模型中需要引入新的变量来解释变化速率上的变异。
1.2 参数估计
在模型(1)中,只假设截距和斜率是随机变量。但一般情况下,模型既有随机斜率,又有固定斜率。固定斜率是不会随观测对象的变化而变化的,因此,更一般的多层模型常常分为随机和固定2部分。用矩阵形式来表述,就得到模型[6]:

其中:Y是结局变量;β是固定系数部分组成的向量;X是对应设计矩阵;u是随机系数部分组成的向量;Z为相应的设计矩阵;向量e代表水平1残差。它们都是模型(1)的矩阵形式,并且有以下假设:

其中:G是随机系数向量u的协方差矩阵;R是残差向量e的协方差阵;V是Y的协方差阵。于是得出似然函数:

再分别对u和β求导,并令结果为0,最后求得u和β的估计:

由此可推出γij等参数的估计。
2 数据描述与处理
本文的数据来源于2003—2008年的《中国统计年鉴》和《中国科技统计年鉴》。涉及的变量如下:
结局变量:lnGDP(生产总值)。它是从2003—2008年我国31个省的地区生产总值的自然对数。这是为了消除异方差性,对原始数据进行的对数转换。
层1解释变量:T(时间)。因为每年测量一次各地区的生产总值,数据搜集时间间隔大致相等,所以可将2003—2008年6个年度的时间分别编码:-5、-4、-3、-2、-1、0。如此编码后,方程截距项就是31个省第6年(2008年)的生产总值的平均值。
层2解释变量:W1(经费利用率);W2(科研人数比例)。W1为2008年各省RD经费占其科技经费筹集总额的百分比。W2为2008年各省科研人数占该省总人口数的比例。
3 GDP影响因素分析
通过研究lnGDP随时间的平均发展趋势,确定GDP与时间呈简单线性关系,而不是二次或更高阶。于是,确定基本模型为线性模型。
3.1 带随机截距的多层线性模型
线性回归模型最简单的扩展是用随机截距代替其固定截距,从而得到以下随机截距多层线性模型:

该模型是为了评价各省GDP的初始水平是否有差别以及数据是否存在层次结构。用spss18整理数据,然后用HLM6.06进行计算,结果如表1所示。

表1 带随机截距的多层线性模型结果
3.2 带随机截距-斜率的多层线性模型
在随机截距模型中,假定每个省GDP初始值不同,但随着时间的变化斜率是相同的,然而实际情况中,各省GDP的发展随着时间变化的斜率是不同的,因此,更符合实际情况的模型应是随机截距和随机斜率模型,模型如下:

组合模型:

计算结果见表2。

表2 带随机截距-斜率的多层线性模型结果
从表2结果可以看出,τ∧00没多大变化,τ∧11=0.000 42(p<0.001),统计显著,表明各省 GDP的发展存在显著差异。
3.3 科技因素的评估模型
为了评价各省科技因素W对GDP的影响,将W1和W2解释变量加入水平2中,得到如下模型:

通过HLM6.06计算,结果见表3。

表3 科技因素评估模型结果

其中:W1(科技经费利用率)对GDP的影响显著,表明科研经费利用率每提高1%,可带动GDP增长0.072 284%;W2(即科技人数比例)对GDP影响不显著,是因为在模型中与科研经费利用率相比,科技人数比例对GDP的影响较弱;W1和W2与时间T没有交互作用,表明GDP每年的增长速率受 W1和 W2的影响较小。而通过对2003—2008年间各省科研经费利用率的研究发现,这些年来各省科研经费利用率几乎没什么变化,这是W与T没交互作用的主要原因。
4 结束语
在以往有关科技和经济的研究中,都是从数量上的变化对其进行研究。本文尝试着从效率的角度分析了科研经费利用率和科技人数比例对经济的影响。利用多层线性模型从纵向角度进行研究,结果表明:科技经费利用率对GDP的影响显著,利用率提高 1%,可带动 GDP增长0.072 284%;科技人数比例对GDP的影响不显著;科研经费利用率对经济的促进作用要显著于科技人数比例对经济的作用。另外,W1和W2与时间T没有交互作用,表明每年的经济增长速率受W1和W2的影响较小。以上结果提示我们,在加大科技投入的同时应努力提高其经费利用率,这样,科技投入对经济的拉动作用才更加显著。
综上所述,多层线性模型适用于经济问题中的纵向研究。
[1]赵志坚.我国科技投入对GDP拉动效应的实证分析[J].经济数学,2008:25(1):58 -63.
[2]李勇敢.科技投入与GDP单位能耗的关系研究[J].创新科技,2010(11):14-15.
[3]葛建军,韩龙.我国第三产业利润率的行业差异分析——基于分层线性模型与最小二乘法的比较[J].贵州财经学院学报,2010(2):56-61.
[4]王济川,谢海义,姜宝法.多层统计分析模型:方法与应用[M].北京:高等教育出版社,2008.
[5]张雷,雷劈,郭伯良.多层线性模型应用[M].北京:教育科学出版社,2003.
[6]Littell R C,Milliken G A,Stroup W W,et al.SAS for Mixed Models(Secend Edition)[M].Cray,NC:SASInstitute Inc,2006:734 -756.
——与非适应性回归分析的比较

