动载荷时域半解析识别方法

陈 帅，杨智春，李 斌，党会学

(西北工业大学 航空学院，西安 710072)

动载荷识别属于结构动力学第二类逆问题研究范畴，主要包括动载荷值的识别及载荷作用部位的识别两方面。

动载荷识别的方法大致可分为频域方法和时域方法两种。目前，动载荷识别的频域方法已趋于成熟，而时域识别方法的问题甚多，为此许多学者在动载荷的时域识别方面开展了许多有意义的工作，例如:基于函数逼近的动载荷识别方法［1－4］、基于模态空间变换与Duhamel积分的动载荷识别方法［5－9］、逆系统动载荷识别方法［10－12］、SWAT 动载荷识别方法［13］以及其它方法［14－16］等。然而，这些方法都存在值得完善的地方，其根源在于动载荷识别这类逆问题在数学上的不适定性:完全依赖于数值方法进行动载荷识别，可能会过多地降低该问题的内在物理约束，而使得其求解条件恶化［5，8－9，17］;相反，仅靠理论分析进行解析求解必然会提高计算的复杂度且降低识别效率，同时受模型简化(包括物理简化与数学简化)方法优劣的影响较大。为提高动载荷识别效率并避免单纯采用数值方法或解析方法等进行动载荷识别的不足，本文结合离散数据拟合与模态空间转换及模态叠加原理，提出一种动载荷时域半解析识别方法，并通过数值仿真与试验验证此方法的可行性。

1 基本方程

1.1 模态坐标函数识别方程

对一个N自由度系统，假设已知其n(n≤N)个自由度的响应，进行模态截断时保留m阶模态，模态坐标函数采用前s阶基函数进行拟合。

对N自由度系统，其物理坐标函数x(t)与模态坐标函数q(t)的转换关系为:

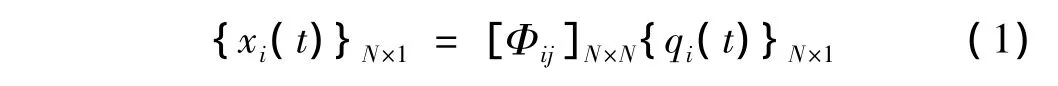
即:

其中:［Φij］N×N=［φ1φ2… φN］，列向量 φ1，φ2，…，φN分别为结构第 1，2，…，N 阶振型，满足 Φij=φj(i)即振型 φj的第 i个分量作为矩阵［Φij］N×N的第 i行第 j列元素。

若已知结构n个自由度的响应，为表述方便，假定已知前n个自由度的响应，则结构物理坐标x(t)与模态坐标q(t)的转换关系缩减为:

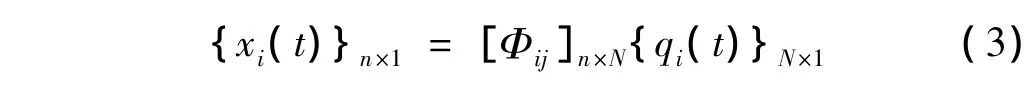
其中:矩阵［Φij］n×N由矩阵［Φij］N×N的前 n 行元素构成。当响应已知的n个自由度并不对应于前n个自由度时，则矩阵［Φij］n×N由矩阵［Φij］N×N中已知自由度对应行的元素构成，并进行重新编号，其它响应的处理方法类似。

进行模态截断，保留m阶模态，则结构物理坐标x(t)与模态坐标q(t)的转化关系进一步缩减为:

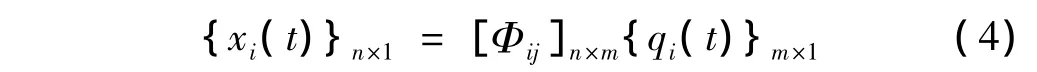
即:

选取一组基函数 T1(t)，T2(t)，…，Tr(t)，…对模态坐标函数q1(t)，q2(t)，…，qm(t)进行最小二乘拟合。

令{Ti(t)}={T1(t)，T2(t)，…，Tr(t)，…}T，并据精度要求截取基函数前r阶进行拟合，则:

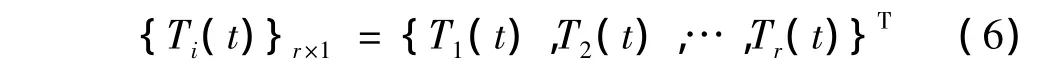
模态坐标函数拟合模型为:

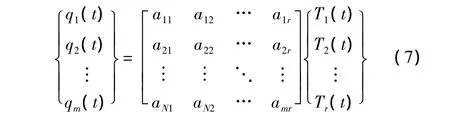
即:

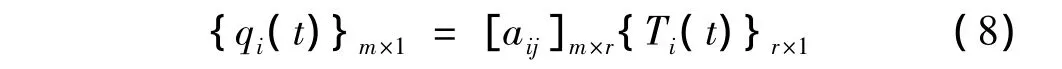
联立式(4)与式(8)，得:

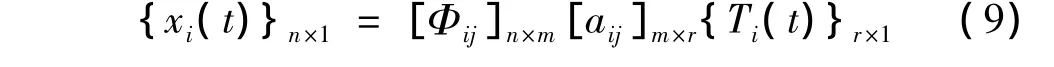
同理，截取基函数 T1(t)，T2(t)，…，Tr(t)，…的前r阶对给定n个自由度的响应x1(t)，x2(t)，…，xn(t)进行最小二乘拟合。其时域响应的拟合模型为:

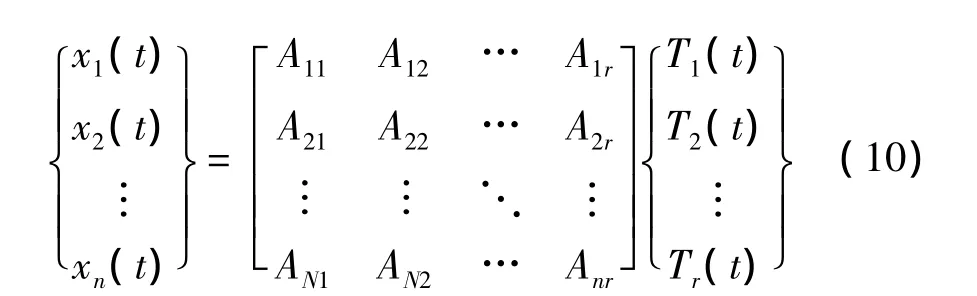
即:

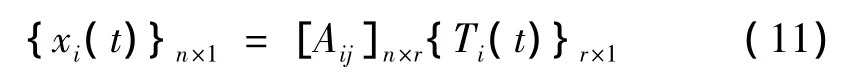
联立式(9)与式(11)，得:

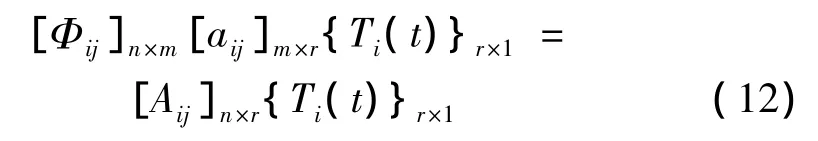
由于{Ti(t)}r×1不恒为零，故要使式(12)在任意时刻t均成立，则应有:

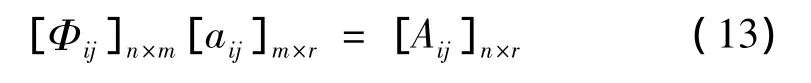
式中:［aij］m×r为待求解的模态坐标函数系数矩阵;［Φij］n×m可由结构固有特性分析获得，也可直接由结构模态试验测试得到;而［Aij］n×r则需利用离散数据曲线拟合方法获得。

利用式(13)求解［aij］m×r，得:

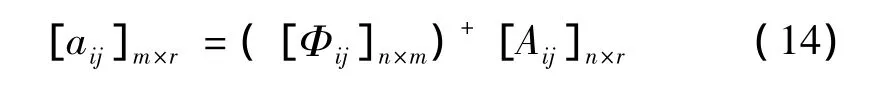
式中(［Φij］n×m)+满足:

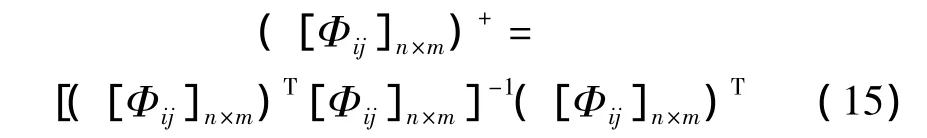
1.2 动态响应识别方程

由坐标变换与模态叠加原理，得:

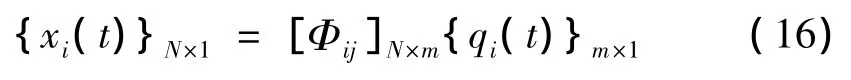
联立式(8)和式(16)，得:

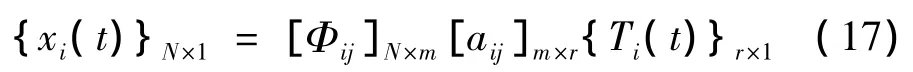
将式(14)代入式(17)，得:

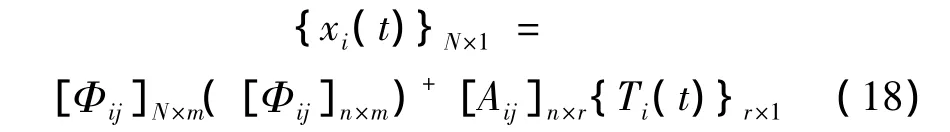
将式(15)代入式(18)，得:

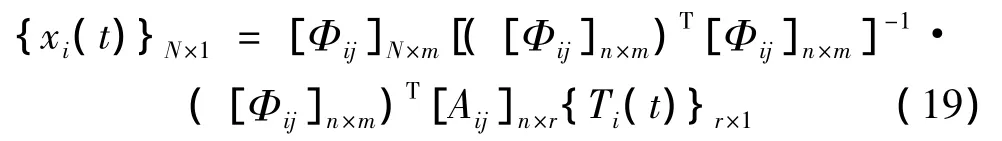
由此便求出由保留模态叠加得到的各自由度时域位移响应函数。对已知某些自由度速度响应或加速度响应的情况，类似的有:

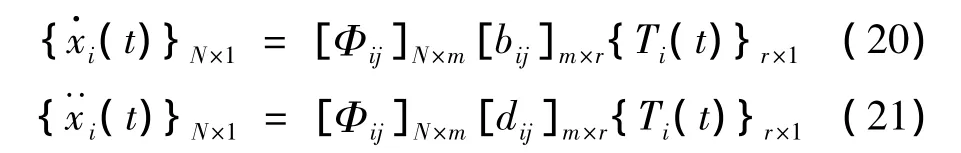
其中:［bij］m×r与［dij］m×r分别为模态速度函数系数矩阵与模态加速度函数系数矩阵。

1.3 动态载荷识别方程

对多自由度系统，其动力学控制方程为:

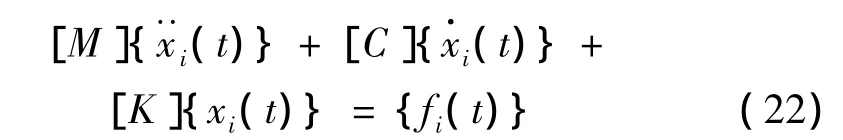
设式(22)描述的运动方程是对结构用有限元方法进行离散化后的方程，并假定用粘性阻尼;而实际上，本文提出的方法并不仅仅针对此种形式表示的结构运动方程，该方法的使用条件为线性系统，即满足模态叠加原理。

按照第1.2节方法识别出位移响应{xi(t)}N×1，速度响应与加速度响应中的任意一种响应后，即可利用这三者间的积分与求导关系及初始条件，得到其它两种形式的响应［18］，而后将其代入运动方程，最终识别出结构各自由度的动态载荷{fi(t)}N×1。

2 数值仿真

图1为典型的20自由度无阻尼质量弹簧系统，其参数及外载荷为:

① 质量:m1=m2=…=m20=1kg;

② 刚度:k1=k2=…=k20=1×104N/m;

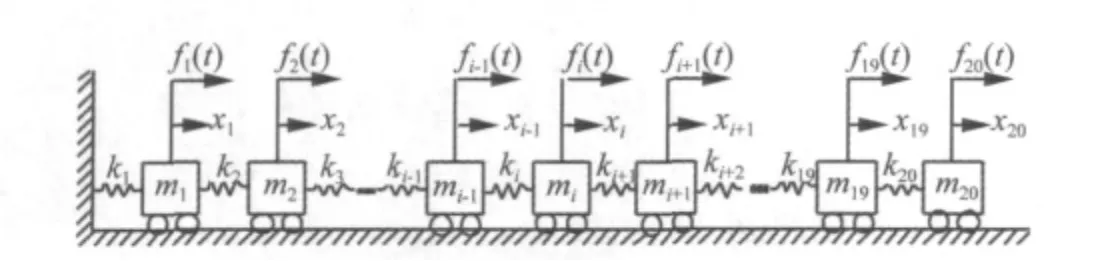
图1 20自由度的无阻尼质量弹簧系统Fig.1 Undamped mass-spring system of20 DOFs

对图1结构按照如下两种工况施加外激励:工况一 单点载荷激励(单位:N):

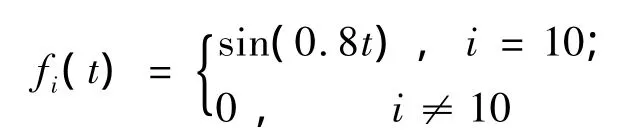
工况二 多点载荷激励(单位:N):

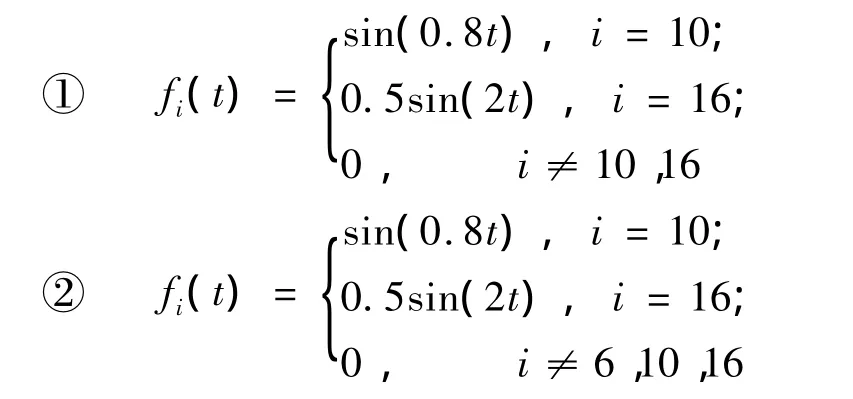
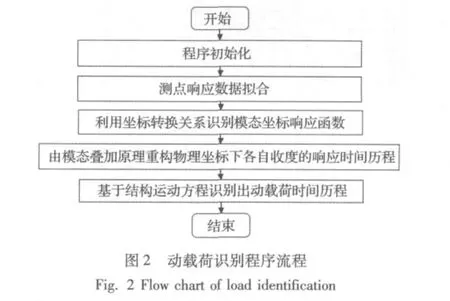
针对上两种工况，利用MSC.NASTRAN计算求解，分别得到该两工况下的时域位移响应，并以此为输入(已知响应)进行动载荷识别。在此采用代数多项式1，t，t2，…，tr，…作为基函数，用最小二乘法进行曲线拟合。不过其基函数并不局限于代数多项式，实际问题中可据需要选择较优的基函数，但其方法的实质并未改变。利用MATLAB软件编程，实现了第1节中的动载荷识别方法，该程序的具体流程如图2所示。

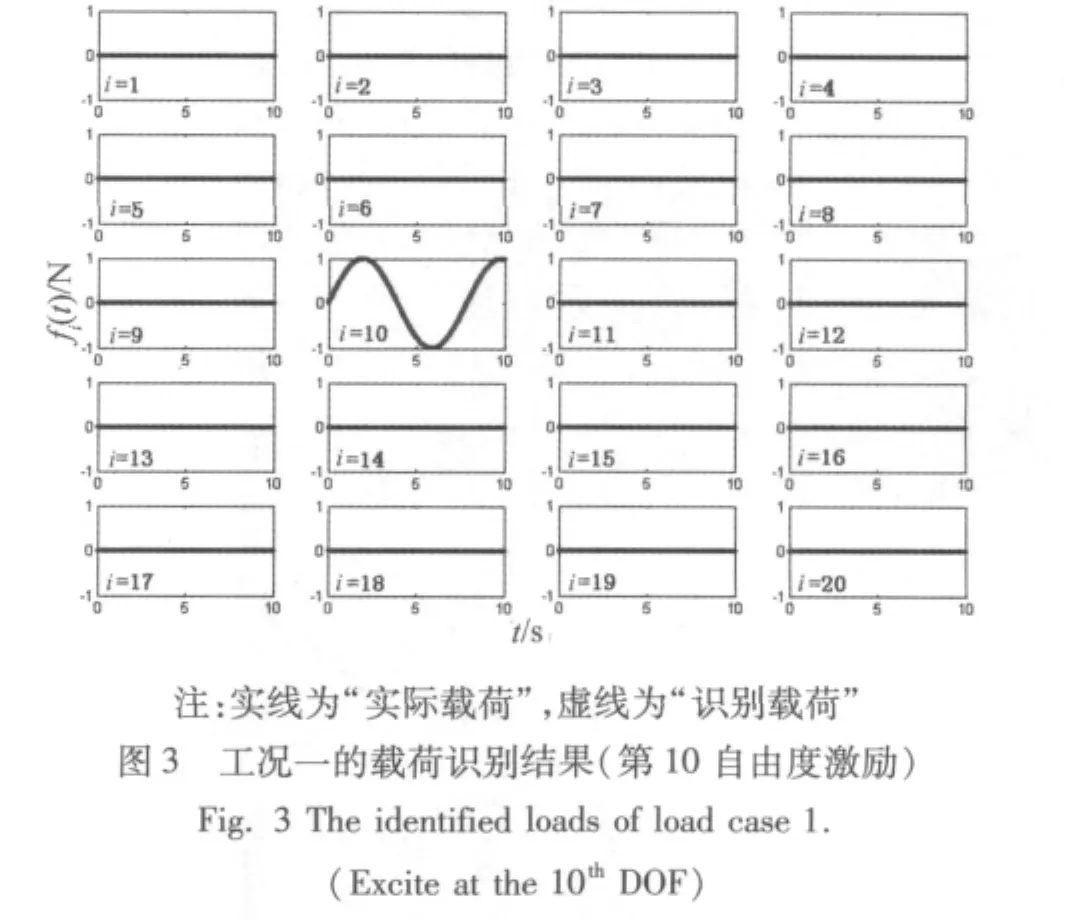
利用编写的动载荷识别程序，可得到本节中各工况下的动载荷识别结果，如图3～图5所示。数值仿真结果表明:

(1)不管是单点载荷激励(工况一)还是多点载荷激励(工况二)，其动载荷的识别结果均与实际载荷吻合较好，进而在一定程度上通过数值仿真论证了该方法的可行性;

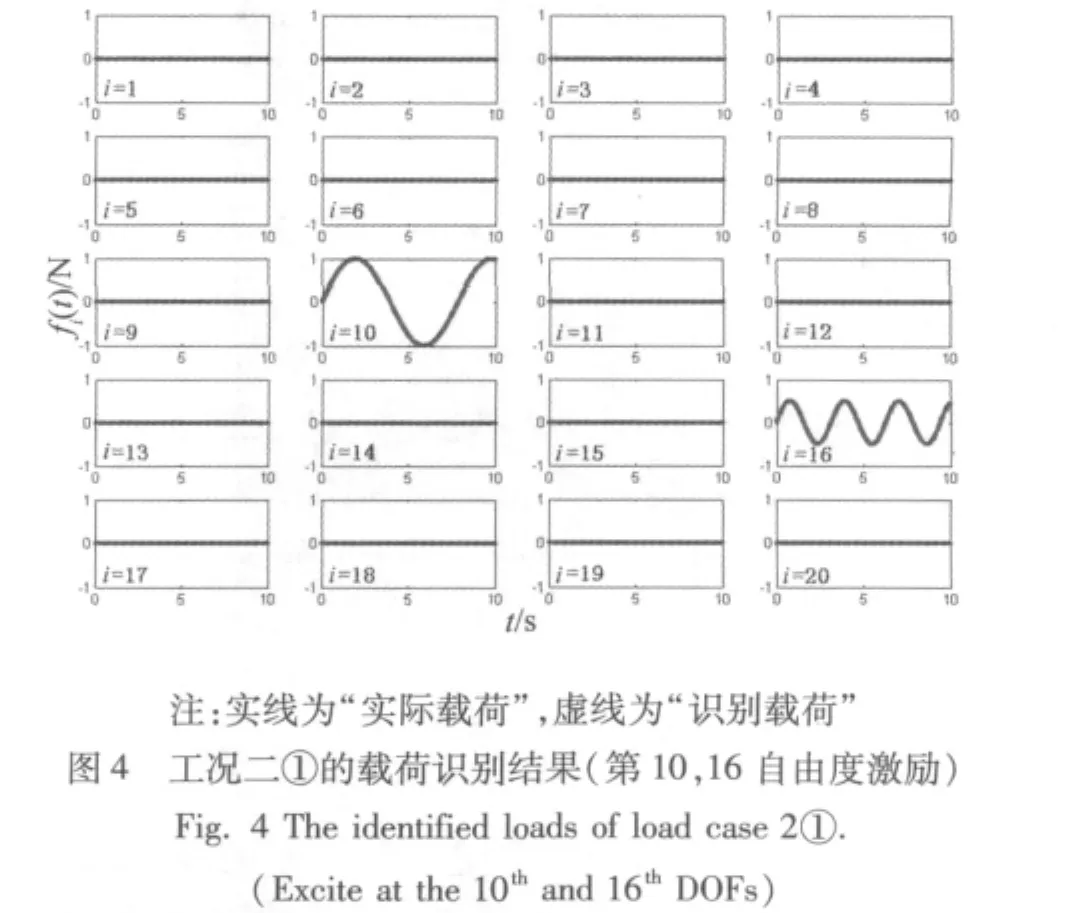
(2)该方法可以较准确地识别载荷的作用位置，因而可用来进行动载荷加载位置识别，特别是对一些具有局部动载荷激励的结构，可用它来进行动载荷的初步定位，进而为确定后续分析中需要详细分析的结构部件或部位提供有效的选择依据;

(3)由于该方法可识别出各自由度上的时域动载荷，因而利用结构有限元方法中的分布载荷与结点载荷之间的转换关系，可进行结构的时域分布动载荷识别。

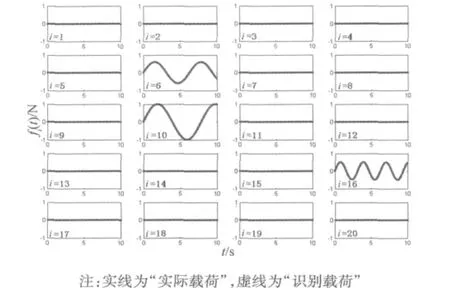
图5 工况二②的载荷识别结果(第6，10，16自由度)Fig.5 The identified loads of load case 2②.(Excite at the 6th，10th and 16th DOFs)

为进一步分析该方法的抗噪能力，针对工况二①的情况，对计算得到的动响应分别人为地增加0%，5%，10%，15%，20%，30%，50%，80%，100% 的随机噪声和高频正弦噪声，并以此为输入识别出其动载荷时间历程，如图6、图7所示。

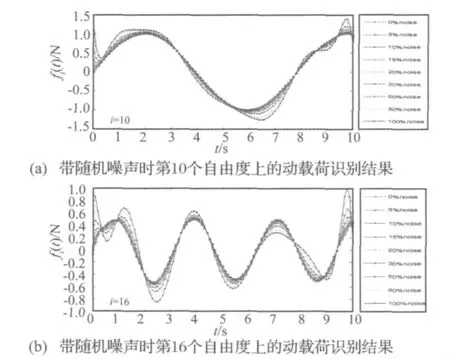
图6 随机噪声下的动载荷识别结果Fig.6 The identified loads with random noise

其中，噪声水平采用定义:

由图6、图7可见，虽然随着噪声水平的增加，其动载荷识别精度有所降低，然而即便是存在某一有用信号完全被噪声淹没的情况，其识别结果仍能具备可接受的精度，且在较低噪声水平下其识别结果比较满意，显然此方法具有良好的抗噪声能力。

3 实验分析

3.1 模型简化与动力学建模

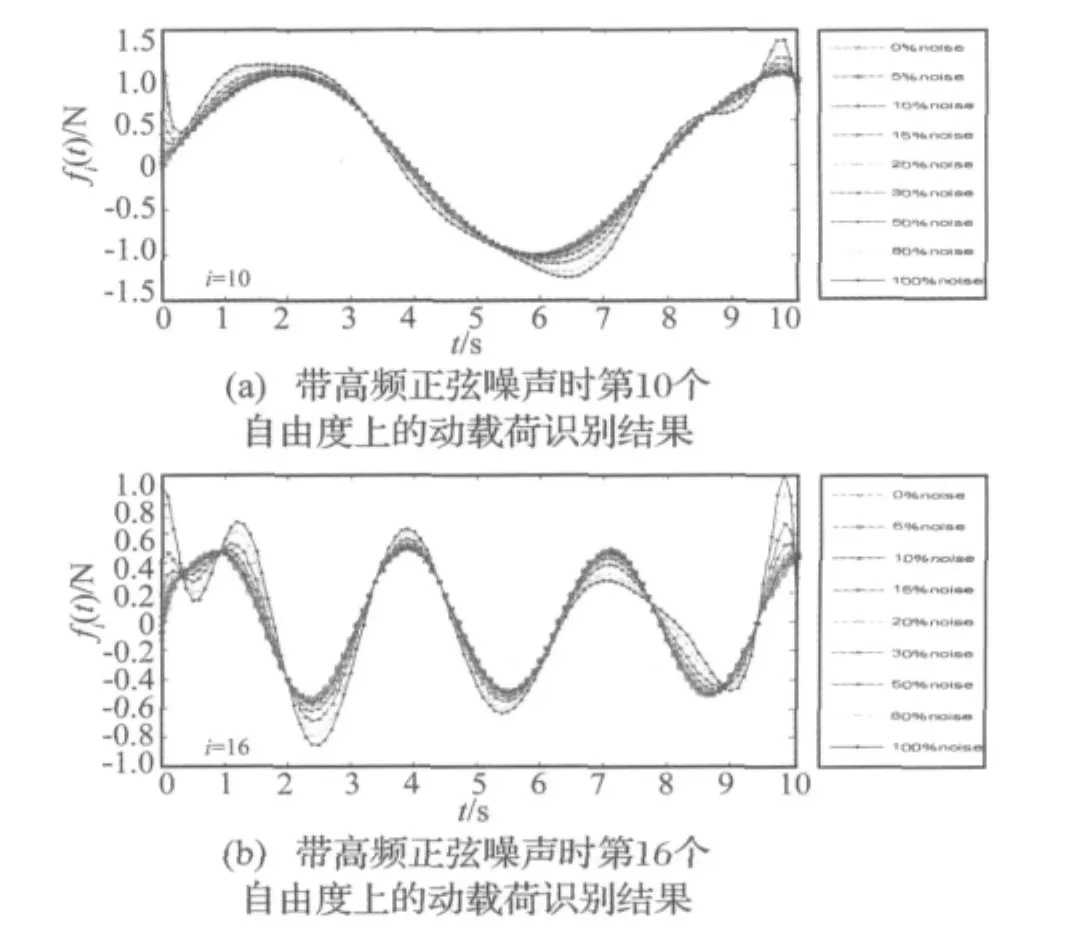
图7 高频正弦噪声下的动载荷识别结果Fig.7 The identified loads with sine noise of high frequency

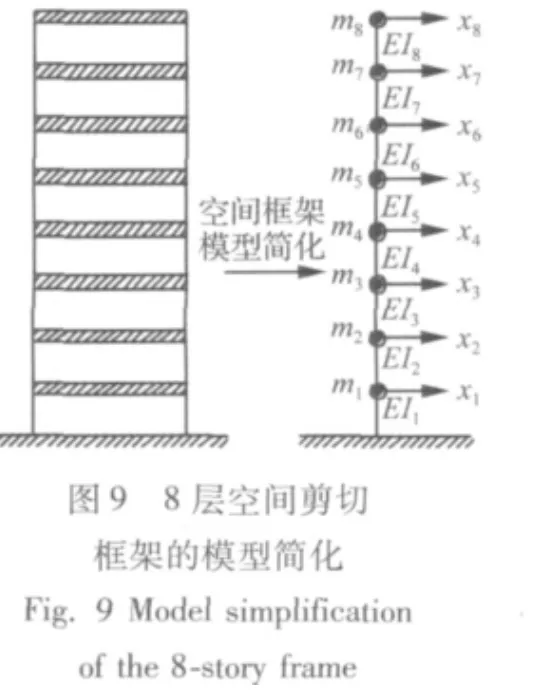
为进一步验证该方法的可行性，设计如图8所示的8层空间剪切框架结构，并对该结构的时域动载荷进行识别。根据该框架的结构特点进行模型简化:① 每层的质量都集中在层间隔框上;② 刚度集中在层间支柱上;③每两层之间有4个支柱，每个支柱由3根截面为 0.139 m ×0.027 m×0.001 m的扁钢层叠而成，其 y方向(宽度方向)的弯曲刚度远大于x方向(厚度方向)的弯曲刚度，只需要考虑其x方向的运动;④ 由于响应测试时间很短且该结构的阻尼较小，因而模型简化时忽略阻尼的作用。

按上述模型简化方法，可得到8层空间剪切框架简化模型如图9所示。

由文献［19］中提出的基于固有频率向量的模型修正方法，得修正后的刚度矩阵与质量矩阵分别为:

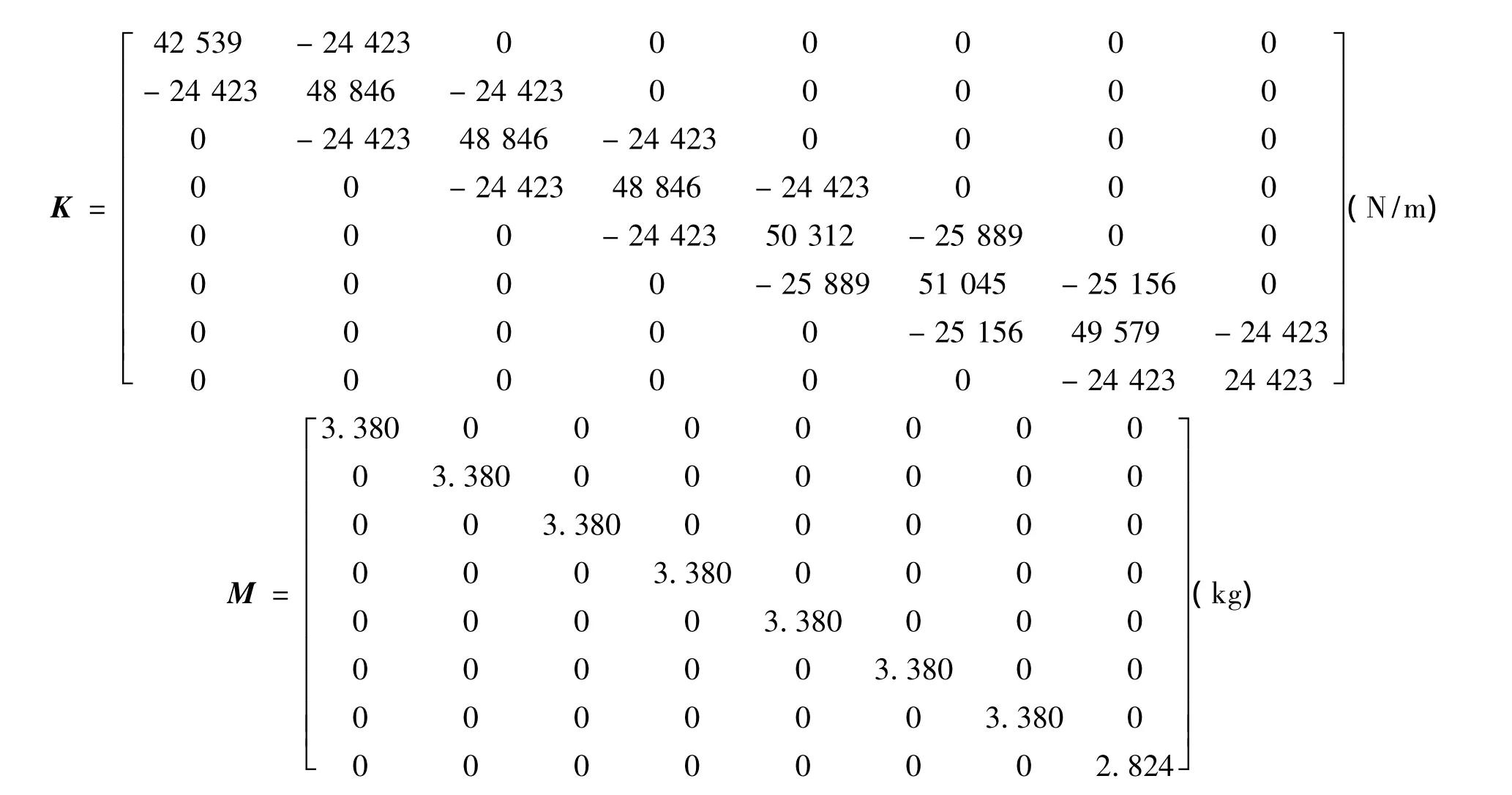
在第一层结构上施加水平方向正弦激励载荷为f1(t)=sin(6πt)(N)，而在其它各层上不进行激励，即当i≠1时 f1(t)=0(N)。

3.2 载荷识别与结果对比分析

针对上述工况，通过试验测试得到该工况下的时域加速度响应，以此作为输入进行动载荷识别。同样，采用基函数多项式 1，t，t2，…，tr，…进行测试动响应拟合，结果如图10所示。

利用MATLAB7.0软件编程，实现了第1节中的动载荷识别方法，得到动载荷识别结果，如图11所示。由图可见，除了少数自由度(第5层)外，基本上也能较好地识别出结构的动载荷。虽然其识别结果存在一定偏差，但基本上也能满足载荷识别要求;同时其误差主要在于载荷识别时使用的是简化模型而非完全真实模型，试验中空间框架仅被简化为8自由度模型，得到的动力学模型简化程度较高，说明对模型简化的优劣必然会对载荷识别的结果产生影响，因而必须在载荷识别前尽可能合理地建立结构的动力学模型。此外，试验测试误差、噪声干扰与拟合基函数类型及阶数的选择也会对载荷识别结果产生一定的影响。

因本算例中结构自由度较少，其动响应可通过测试获得，已知信息较充分，故载荷识别结果很好;但考虑实际结构自由度较多且无法测试获得全部动响应，因此为分析响应测点位置的选择对载荷识别结果的影响，任意选择三组测点进行加速度响应测试:① 第1，2，3，5，6，8 自由度，② 第 1，2，4，6，7，8 自由度，③ 第1，3，4，5，7，8 自由度;分别将所选测点处的测试加速度为输入进行载荷识别，得到的动载荷识别结果如图12所示。

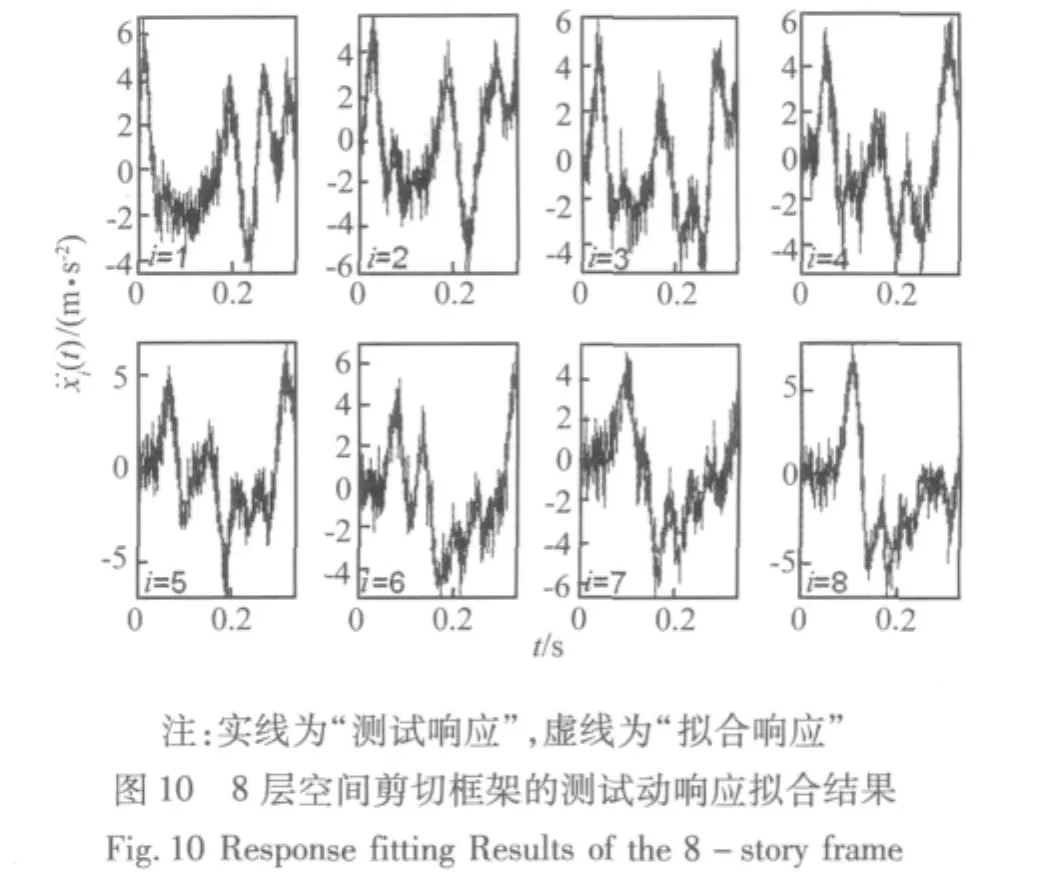
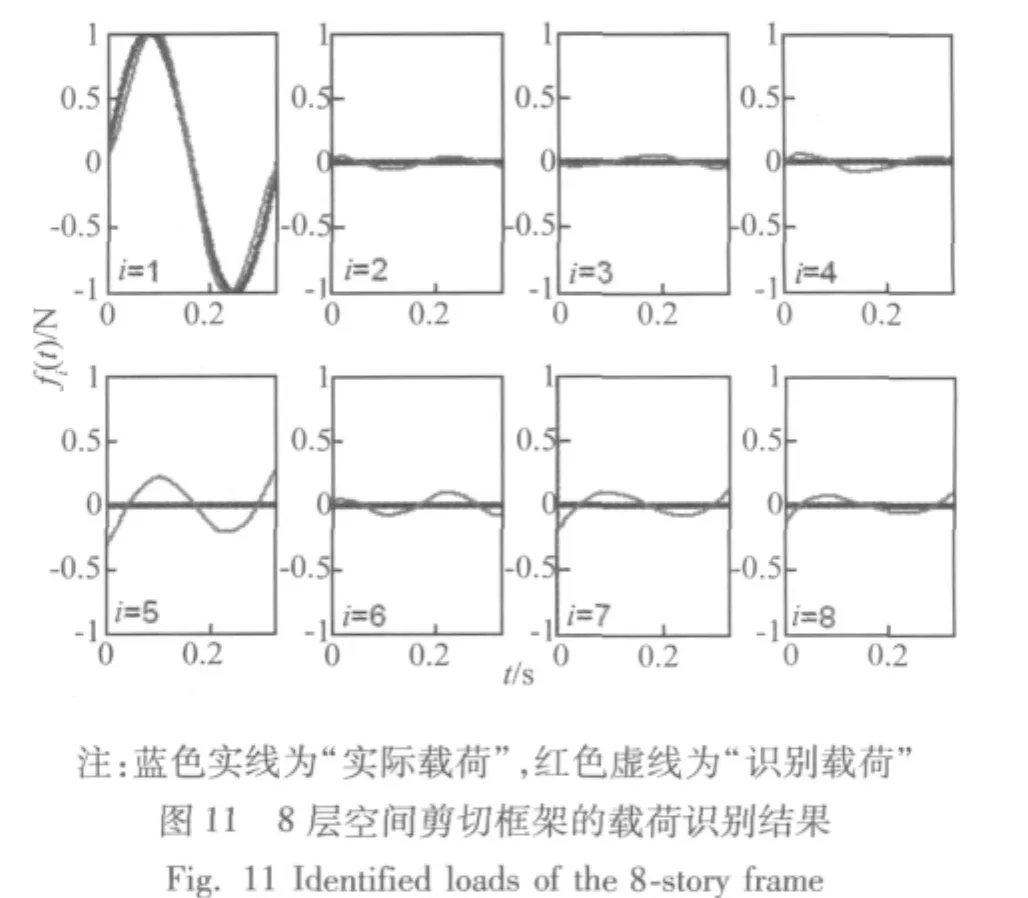
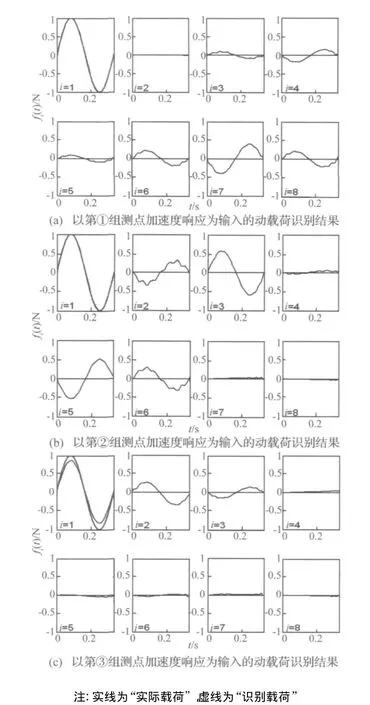
图12 响应测点不够时8层空间剪切框架的载荷识别结果Fig.12 Identified loads of the 8-story frame without enough testing points of response

由图12可见，在第③种输入情况下除少数自由度上的载荷识别误差相对较大外，其它自由度的载荷识别结果较好;而在第①种、第②种输入情况下，与其他相比载荷识别精度较低。结果表明，当测试响应不全(即已知信息缺失)时，载荷识别精度会降低，甚至产生较大误差，此问题主要是由于在约束不足的情况下使用［Φij］n×m的广义逆阵进行未知自由度响应重构所得到的是最小二乘解，且考虑到测试中存在噪声与误差，而各自由度测得的有用信号成分与干扰信号成分(噪声成分及测试误差成分等)的比例各不同，显然所选测点组的有用信号成分比例越大，其获得的动载荷识别精度越高;同时，识别结果的好坏与响应测点位置的选择有关，合理地布置测点能改善识别精度，因此需要采用优化方法进行专题研究。实际应用中，测试响应不全的问题在数学及物理上只凭借测试有限自由度的响应通常都是无法彻底解决的，依靠现有的各种方法得到的动载荷仅为工程可用解(本例中是最小二乘解)，是一种在有限约束下的等效载荷，而并非一定是真实解。要得到真实的动载荷则必须根据实际情况增加相应约束，考虑到结构本身具有的滤波作用，并非所有成分载荷都能引起显著的结构响应，因而在实际应用中识别出一组相对较优的工程可用载荷也同样具有重要意义。

4 结论

为提高动载荷识别效率并避免单纯采用数值方法或解析方法进行动载荷识别的不足，本文结合离散数据拟合与模态空间转换及模态叠加原理，提出了一种动载荷时域半解析识别方法。

以数值仿真响应为输入的动载荷识别结果表明:无论是单点载荷还是多点载荷，该方法均能较好地实现结构动载荷大小与作用位置识别;同时，它还具有较好的抗噪声干扰能力;此外，还可利用结构有限元方法中的分布载荷与结点载荷之间的转换关系，进行结构时域分布动载荷识别，即具有一定的拓展潜力。而以试验测试加速度响应为输入的动载荷识别实例结果表明:该方法对动载荷识别的优劣程度，受模型简化优劣程度、响应测点布置等因素影响，合理简化模型与响应测点选择是比较关键的。此外，试验测试误差、噪声干扰与拟合基函数类型及阶数的选择也会对载荷识别结果产生影响。

［1］张 方，秦远田，邓吉宏.复杂分布动载荷识别技术研究［J］.振动工程学报，2006，19(1):81－85.

［2］秦远田，张 方.具有连续分布梁模型动载荷的识别技术研究［J］.振动与冲击，2005，24(2):126－128，133.

［3］张 方，朱德懋.动态载荷时域识别的级数方法［J］.振动工程学报，1996，9(1):1－8.

［4］王彦卫，赵 玫.一种新的动态载荷识别方法［J］.噪声与振动控制，2003，3:11－13.

［5］初良成，曲乃泗，邬瑞锋.动态载荷识别的时域正演方法［J］.应用力学学报，1994，11(2):9－18.

［6］蔡元奇，朱以文，刘礼华.动态载荷识别中的模态确定方法研究［J］.振动工程学报，2006，19(4):543－547.

［7］张运良，林 皋，王永学，等.一种改进的动态载荷时域识别方法［J］.计算力学学报，2004，21(2):209－215.

［8］Jiang X Q，Hu H Y.Reconstruction of distributed dynamic loads on an euler beam via mode-selection and consistent spatial expression［J］.Journal of Sound and Vibration，2008，316:122－136.

［9］Jiang X Q，Hu H Y.Reconstruction of distributed dynamic loads on a thin plate via mode-selection and consistent spatial expression［J］.Journal of Sound and Vibration，2009，323:626－644.

［10］魏星原，宋 斌，郑效忠.载荷识别的逆系统方法［J］.振动、测试与诊断，1995，15(3):35－43.

［10］蔡元奇，朱以文.基于逆向滤波器的动态载荷时域识别方法［J］.振动工程学报，2006，19(2):200－205.

［12］饶柱石，施勤忠，荻原一郎.基于逆系统分析法的多输入－多输出系统动态载荷的优化估计［J］.振动与冲击，2000，19(2):9 －12，16.

［13］路敦勇，吴 淼.动态载荷识别的SWAT方法研究［J］.振动与冲击，1999，18(4):78－82，94.

［14］毛玉明，郭杏林，赵 岩，等.基于灵敏度分析的结构动态载荷识别研究［J］.振动与冲击，2010，29(10):1－3.

［15］赵玉成，袁树清，李瞬酩，等.动态载荷的小波正交算子变换识别法［J］.机械强度，1998，20(2):127－130，133.

［16］毛玉明，郭杏林，赵 岩，等.基于精细计算的动载荷反演问题正则化求解［J］.动力学与控制学报，2009，7(4):308－312.

［17］刘恒春，朱德懋，张久厚.振动载荷识别的奇异值分解法［J］.振动工程学报，1990，3(1):24－33.

［18］胡以怀，周秩尘.载荷识别中振动响应的简易获取［J］.武汉交通科技大学学报，1994，9(3):247－250.

［19］王 乐，杨智春，李 斌，等.基于固有频率向量的模型修正方法［J］.西北工业大学学报，2008，26(1):93－98.