超音速弹翼非线性颤振分析与控制

贾尚帅，丁 千，刘 炜

(1.天津大学 机械学院力学系，天津 300072;2.中国航天科工集团公司 二院二部，北京 100854)

随着现代飞行器性能的提高和设计技术的发展，气动弹性研究变得愈加重要。对于气弹动力学稳定性问题(颤振分析)，已经由最初经典的线性颤振分析逐步拓展出非线性颤振分析等新的内容和分支，非线性颤振系统可以表现出丰富的动力学行为，常常出现极限环、分岔、混沌等复杂非线性现象［1］，这些现象会直接导致飞行器结构的破坏，造成极大的安全隐患。因此非线性气动弹性颤振分析与主动控制成为重要的研究领域［2］。

非线性气动弹性领域主要研究气动非线性和结构非线性。其中结构非线性主要包括立方非线性、间隙非线性和迟滞非线性。郑国勇等［3］基于活塞理论研究了带有立方非线性俯仰刚度二自由度机翼系统在典型参数下的稳定极限环颤振及混沌响应。Abbas等［4］用数值方法系统的研究了超音速、高超音速下沉浮和俯仰同时具有间隙和三次刚度非线性的双楔形翼面的非线性气弹问题。赵永辉等［5］分析了亚音速、不可压缩流作用下带有操纵面间隙非线性的翼段结构的气动弹性响应。目前对非线性颤振主动控制问题的研究大都局限于连续的立方非线性［6－7］，关于间隙等不连续非线性系统如何实现颤振主动控制研究相对较少，文献［8］对间隙不连续非线性系统的颤振主动控制进行分析，但并未考虑气动力非线性的影响。

本文基于三阶活塞理论，充分考虑结构间隙非线性和非线性气动刚度的影响，分析超音速弹翼的颤振特性，并基于微分几何法和二次型最优控制进行主动控制，研究系统的气动弹性稳定性。

1 非线性气动弹性模型

1.1 非线性结构模型

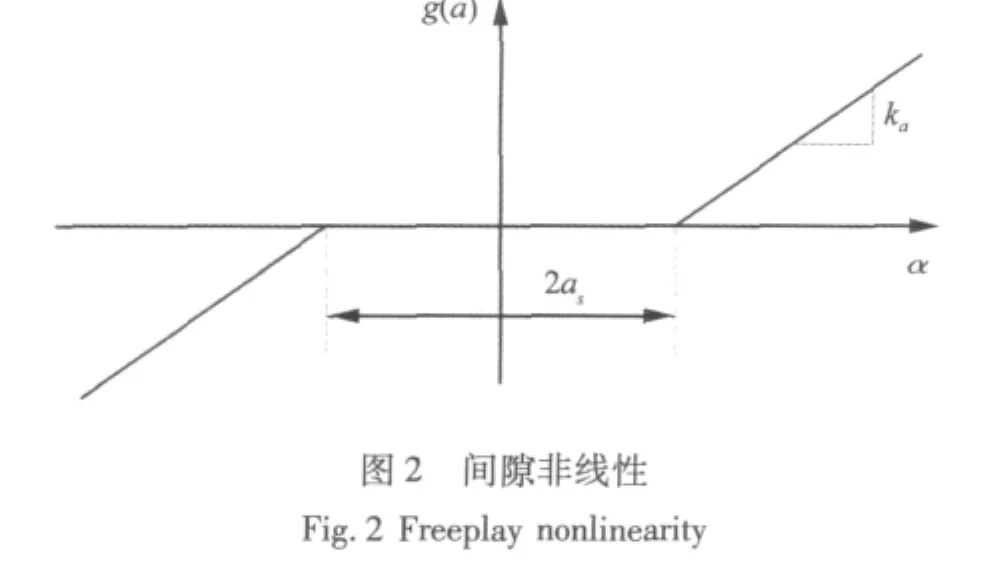
对于间隙非线性的研究，大都是针对具有沉浮和俯仰的两自由度二维翼段，如图1。俯仰自由度的间隙非线性施加如图2所示。

利用拉格朗日方程得到翼段的气动弹性运动微分方程:

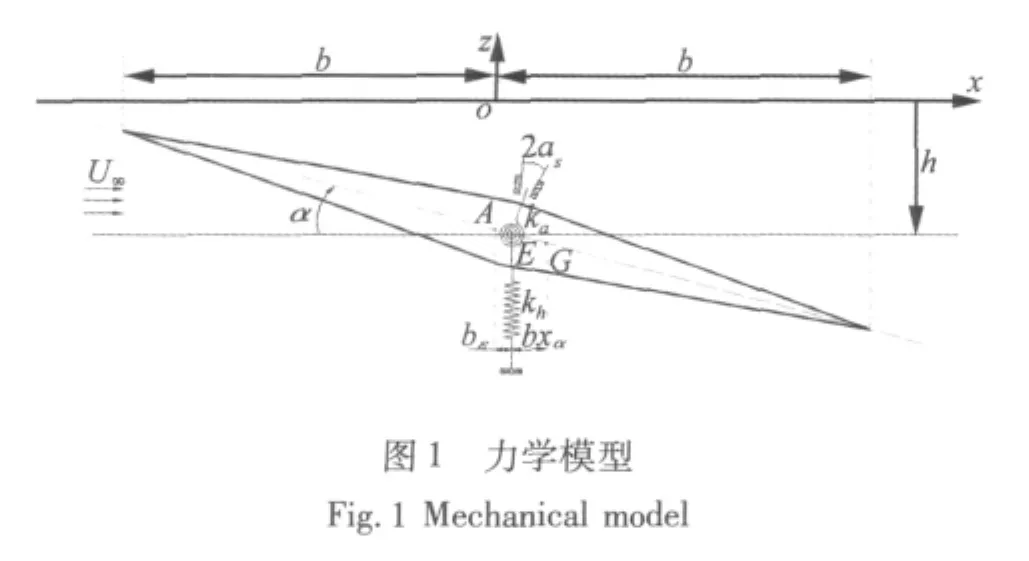
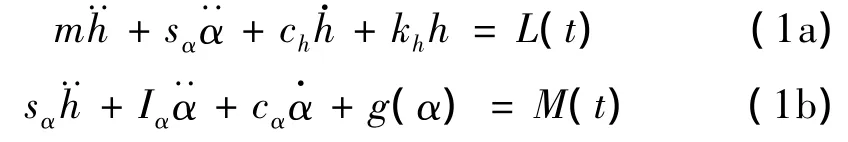
其中:h为弹性轴沉浮位移，向下为正;α为翼段俯仰角，抬头为正，m，sα，Iα分别为单位展长弹翼的质量、对弹性轴的质量静矩及对弹性轴的质量惯性矩，ch，cα分别为弹翼的沉浮与俯仰阻尼系数，kh，kα为沉浮与俯仰刚度，g(α)为扭簧扭矩，L，M为气动升力与力矩。b为半弦长，2αs为扭转间隙，bχα为重心G到弹性轴E的距离，bε为中心A到弹性轴E的距离。

1.2 超音速非定常气动力

采用三阶活塞理论能较好地体现气动力的非线性效应［9］，主要考虑非线性气动刚度影响:

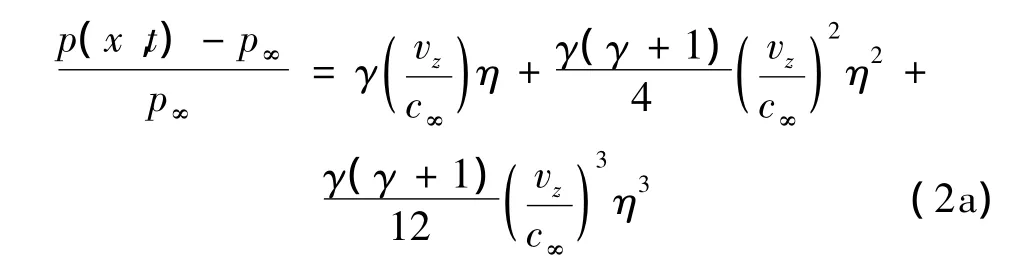
上下翼面任意点的下洗速度:

其中:

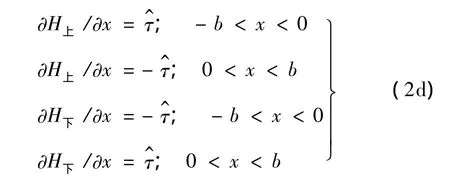
式中:γ为比热比，η为空气动力修正因子，p∞，c∞分别为自由来流压强及声速，vz为垂直于来流翼面某点处的下洗速度，U∞为自由来流速度，H(x)为翼型函数，τ^为翼型斜率。

上下翼面压力差:

综合式(2)将Δp向弹性轴E点简化，得空气升力与气动力矩:

1.3 无量纲非线性气动弹性模型

无量纲化的动力学方程为:

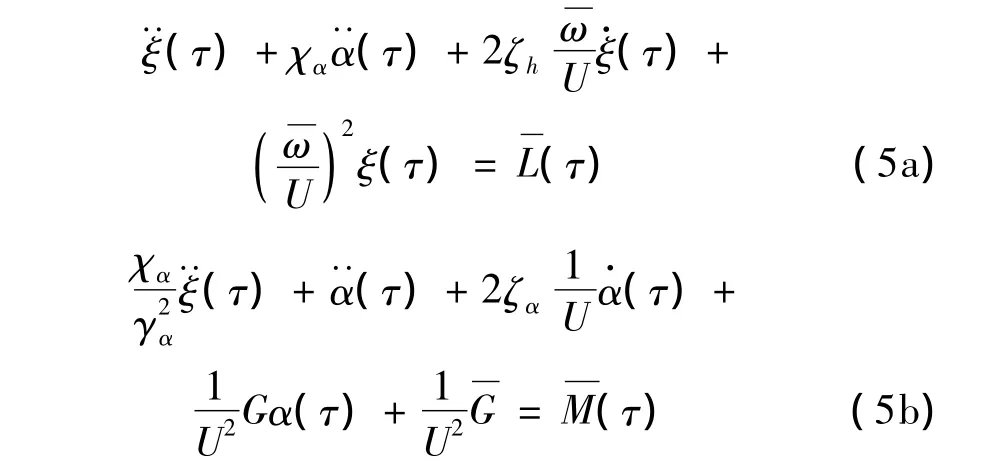
其中:

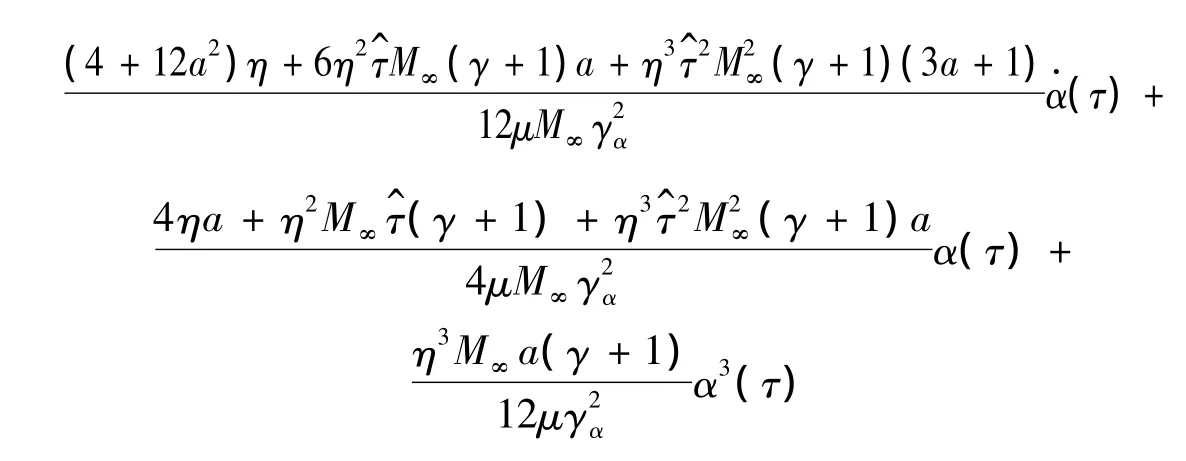
2 颤振分析

2.1 分岔点及分岔确定

弹翼颤振是在结构的弹性力、惯性力与气动力耦合作用下，因气动弹性失稳而产生的自激振动，是一种典型的Hopf分岔。超临界Hopf分岔是当飞行速度超过失稳速度(分岔点)后产生的、幅值缓变的极限环振动，危害性相对较小。亚临界Hopf分岔则是在速度还未达到分岔点时，由于较大的环境扰动而产生的、幅值较大的极限环振动，极限环振动会引起结构疲劳，危害性较大。

其中:U为无量纲飞行速度，并且:

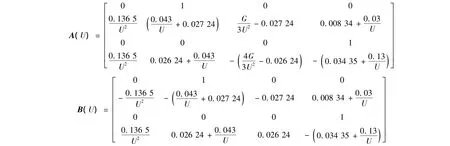
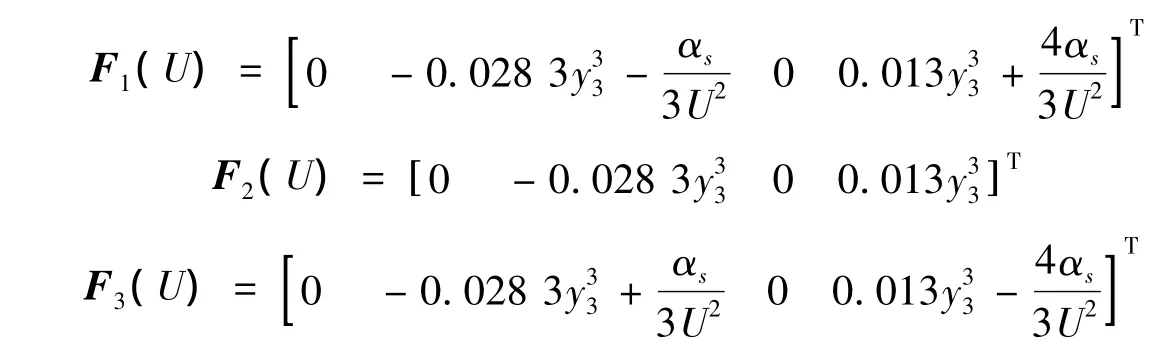
系统参数取值如表1所示。

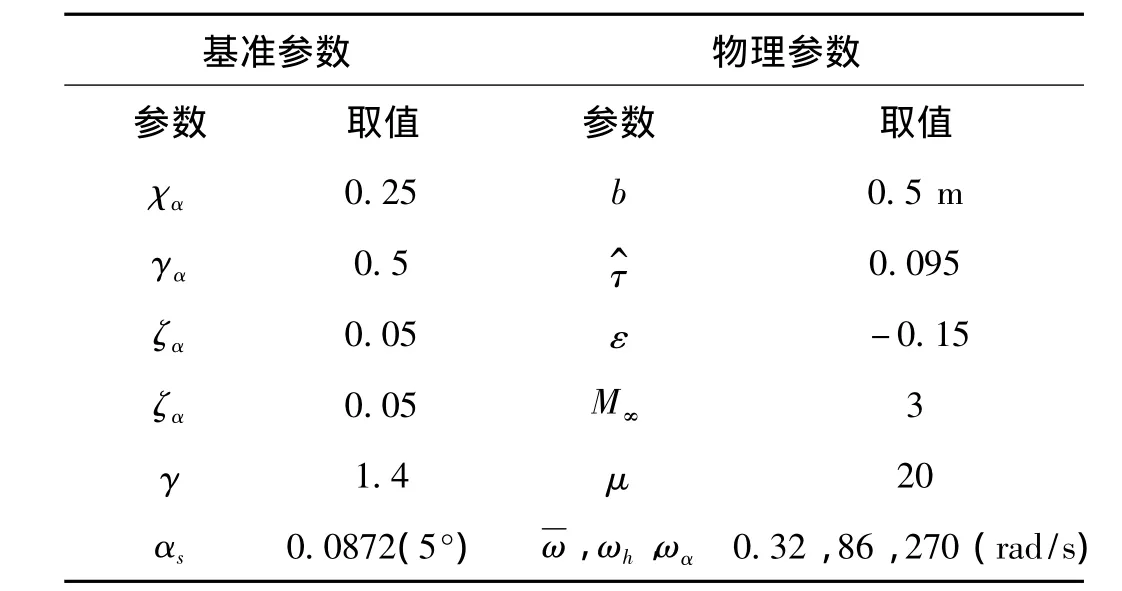
表1 系统参数Tab.1 System parameters

翼段方程(6b)描述系统受到最小扭簧扭矩作用的运动，其平衡点O(0，0，0，0)的稳定性最弱。显然，O点的Jacobi矩阵即B(U)，其特征多项式为Det(B－λI)=0，可写成方程:

其中:

当来流速度增大至U=Uhopf，系数满足b0＞0及条件:

式(7)有一对纯虚根及一对负实部特征根。根据Routh-Hurwitz定理，当U＞Uhopf时系统的平衡点失稳，产生自激周期振动，Uhopf成为临界颤振速度。

由表1中的模型参数计算，可得系统平衡点失稳的临界颤振速度Uhopf及对应的特征根:

式(7)的特征根为± 0.1607i，－ 0.1532，－0.0125。

2.2 亚临界颤振特性分析

根据等效线性化理论［10］，中心型间隙模型描述:

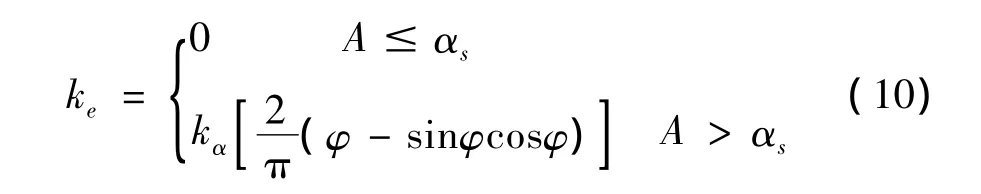
其中:φ =cos－1(αs/A)，A 为俯仰方向的振幅，kα为无间隙俯仰刚度，ke为俯仰等效刚度，如图3所示。

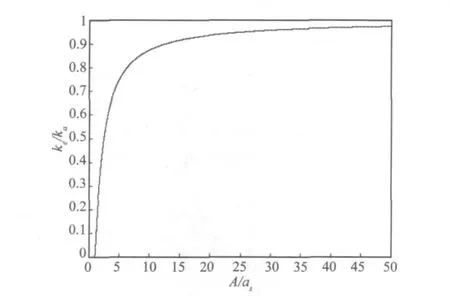
图3 俯仰刚度Fig.3 Pitch stiffness

间隙翼面俯仰刚度ke在超过间隙后由零值迅速增加，而后缓慢趋向于无间隙刚度kα，正是这种刚度上的变化，使得系统与不具有间隙的弹翼颤振不同，其表现为典型的非线性亚临界颤振的特性。进一步分析可以得到亚临界分岔点，对应最小颤振速度为:

此时所对应的ke/kα=0.12，相应的弯扭频率比为ωh/ωe=1/1.09，正是这种频率上的重合使得亚临界点的颤振速度变的很低。

3 基于微分几何法的非线性颤振控制

3.1 控制器设计

基于式(6b)是导致系统出现极限环振动的原因，对于分段非线性系统(6)，可以进行分段非线性控制，针对系统的状态方程(6b)，设受控的非线性系统为:

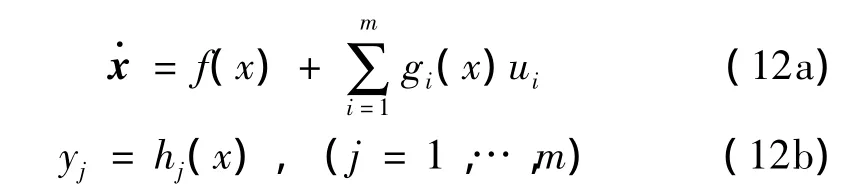
考虑输入与输出数相等的情况，取m=2的多输入多输出控制系统:

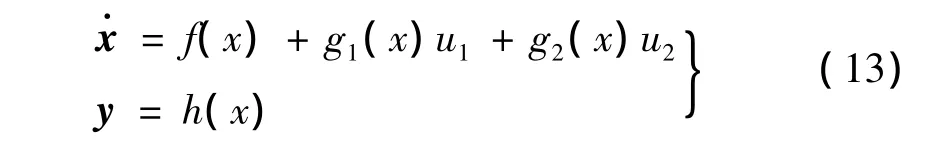
其中:

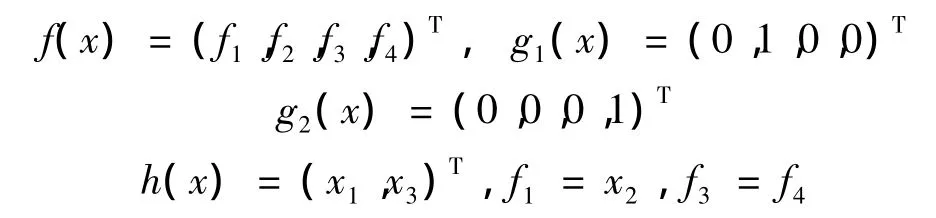
应用微分几何法，通过非线性状态反馈与坐标变换，将非线性系统精确线性化:

其中:

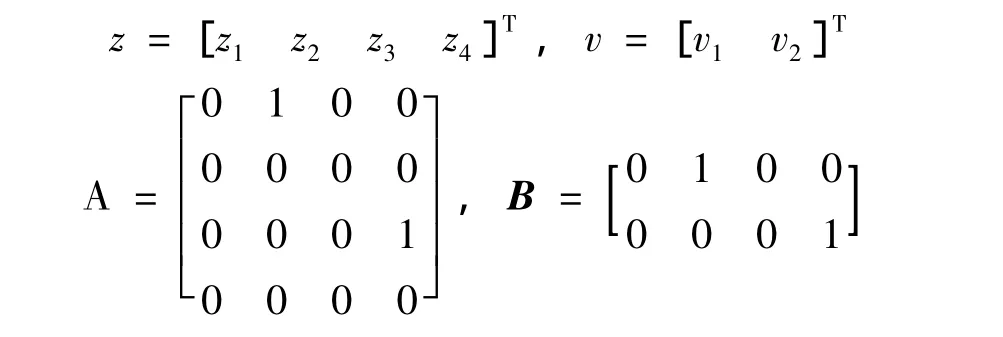
人为输入v作为线性极点配置控制器的输入，可保证整个系统的稳定性。

3.2 基于二次型最优控制

定义系统二次型性能泛函为:

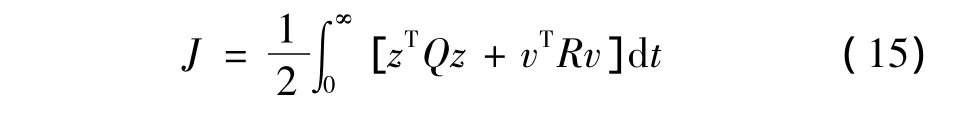
式中:Q，R分别为对状态变量与输入变量的加权矩阵，Q为半正定矩阵，R为正定矩阵。

二次型最优控制即对系统(14)确定最优控制输入规律，即:

式中:K为状态反馈增益矩阵，使二次型性能指标最小。反馈增益矩阵可表示为:

P应满足黎卡提代数方程:

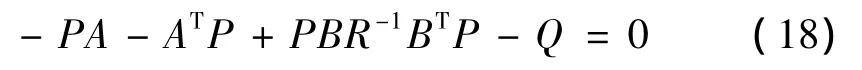
最优控制率为:

4 仿真结果

令状态权矩阵 Q=δQdiag(Q11，0，Q33，0)，控制权系数R=δRI，其中I为2×2的单位矩阵，Q11和Q33为对应沉浮位移和俯仰角度权重，δQ和δR为对应状态权矩阵Q和控制权系数R的性能指标系数。分别取Q11=10－6，Q33=10－4，δQ=10，δR=1 时，可以得到受控制系统的临界颤振速度:

图4～图8为原系统与受控系统的时间响应、相图及分岔点与控制参数的变化曲线。图4为U=1.6时，原系统和受控系统均稳定收敛到零点，相比而言受控系统的响应时间更短。图5为U=1.7时，原系统发生颤振，产生极限环，但此时受控系统仍然收敛到零点。图6为U=2.0时，原系统与受控系统均为极限环振动，而受控系统的振幅比原系统的振幅减小。图7为U=1.28时，在较大扰动下，原系统对应亚临界颤振而受控系统稳定收敛。图8为改变状态权矩阵和状态权系数时，对系统临界颤振速度的影响，随着δQ的增大系统的临界颤振速度和亚临界分岔点均有所提高，而对应减小δR能够得到相同的结果。

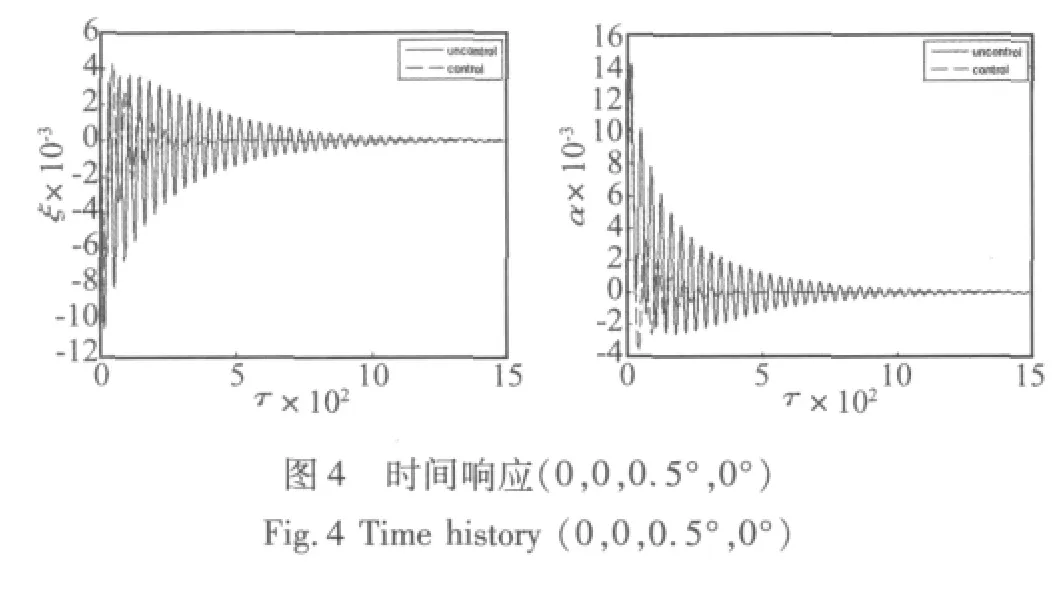
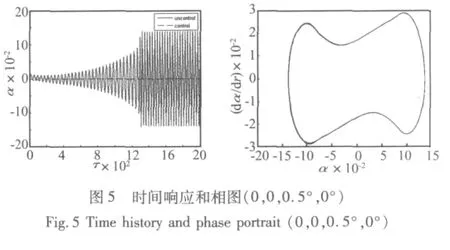
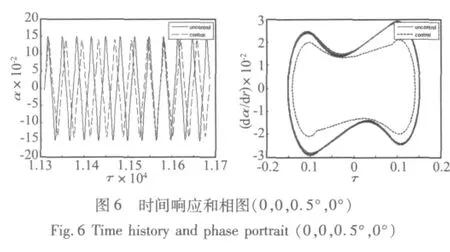
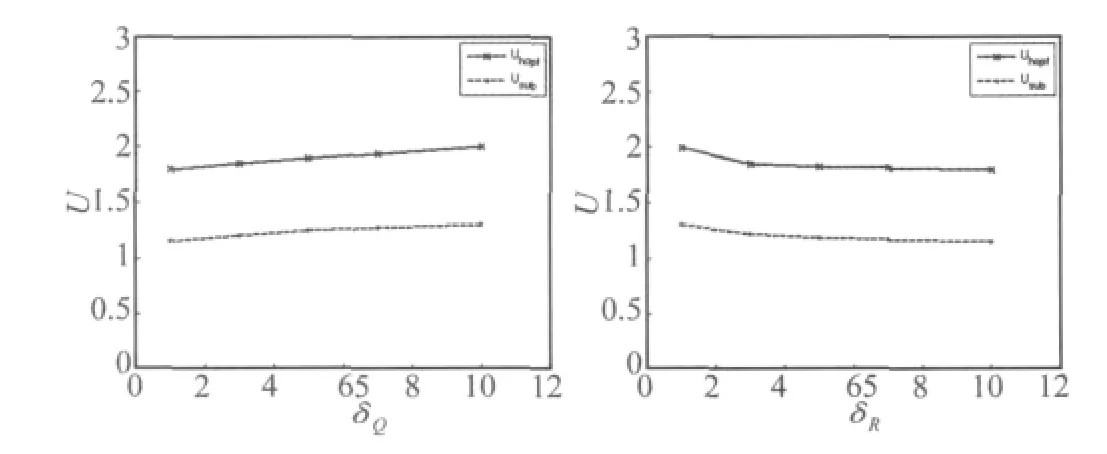
图8 分岔临界速度与控制参数Fig.8 Bifurcation critical speed vs.control parameters

5 结论

研究超音速含间隙弹翼的颤振特性及控制，应用基于微分几何法与二次型最优控制相结合的方法，设计非线性控制器。研究结果表明:

(1)超音速含间隙弹翼的颤振在考虑非线性气动刚度的影响下为典型的亚临界颤振;

(2)基于微分几何法和二次型最优控制相结合的非线性控制器，不会改变系统亚临界颤振特性，但可以提高系统的临界颤振速度，减少颤振结构疲劳破坏;

(3)通过调节Q，R的性能指标系数能改变系统的响应特性，提高含间隙弹翼的气动弹性稳定性。

［1］Lee B H K，Price S J，Wong Y S.Nonlinear aeroelastic analysis of airfoils:bifurcation and chaos［J］.Progress in Aerospace Sciences，1999，35:205 －334.

［2］Mukhopadyay V.Historical perspective on analysis and control of aeroelastic responses［J］. Guidance Control Dynamic，2003，26:673 －684.

［3］郑国勇，杨翊仁.超音速流中结构非线性二元机翼的复杂响应研究［J］.振动与冲击，2007，26(12):96－100.

［4］Abbas L K，Chen Q，Donnell K O，et al.Numerical studies of a non-linear aeroelastic system with plunging and pitching freeplays in supersonic/hypersonic regimes［J］.Aerospace Science and Technology，2007，11(5):405 －418.

［5］赵永辉，胡海岩.具有操纵面间隙非线性二维翼段的气动弹性分析［J］.航空学报，2003，24(6):521－525.

［6］丁 千，王冬立.用规范型直接法研究立方非线性机翼的颤振［J］.飞行力学，2005，23(3):85－88.

［7］Bhoir N，Sigh S N.Control of unsteady aeroelastic system via state-dependent riccati equation method［J］.Journal of Guidance，Control，and Dynamics，2005，28(1):78 －84.

［8］李道春，向锦武.间隙非线性气动弹性颤振控制［J］.北京航空航天大学学报，2007，33(6):640－643.

［9］Librescu L，Marzocca P，Silva W A，et al.Supersonic/hypersonic flutter and postflutter of geometrically imperfect circular cylindrical panels［J］.Journal of Spacecraft and Rockets，2002，39(5):802 －812.

［10］胡寿松.自动控制原理［M］.北京:科学出版社，2001.