基于单元残余能量灵敏度的结构损伤识别

吴合良，谢居静，熊 造

(1.湖南省大岳高速公路建设开发有限公司，岳阳 414000;2.湖南中大设计院有限公司，长沙 410075)

灵敏度分析研究模型输出受各种输入变化的影响及模型本身受输入信息的影响。由于其诊断性和预测性，故将灵敏度分析看做建模与模型分析的先决条件［1］。作为分支，结构动态特性灵敏度分析，也是结构优化设计的主要研究内容之一。目前，结构动态特征灵敏度分析主要集中在结构自振频率及振型的灵敏度分析上，而对由基本模态参数衍生出的指标的灵敏度分析相对较少。研究表明，衍生出的指标对结构参数更为敏感［2］。近年来，基于能量指标的结构损伤识别方法得到广泛关注，如模态应变能、残余能量、能量传递比、伪比能等。Shi等［3－4］采用模态应变能的变化率作为结构损伤指标，在梁结构与平面刚架结构的损伤定位及损伤程度判别方面的研究有些成效;Alvandi［5］指出应变能指标无论对单一损伤工况或多点损伤工况的损伤位置识别结果均优于其它指标，并且在含噪声情况下损伤定位结果的稳定性最好。由于求解应变能时必须用到完整的振型，应变能法仍摆脱不了需要进行振型扩展的不足。Huang等［6］提出了能量传递比(ETR)进行损伤定位的指标。Law等［7］认为在同样能量输入条件下结构损伤前后的总能量守恒。单元应变能的增加，意味着单元动能的减少，以单元应变能与动能之比(能量商)作为指纹比单独使用单元应变能对损伤更为敏感。利用损伤前后单元能量商的变化可实现损伤定位。黄方林等［8］定义了一种与结构故障有关的特征参数—残余能量，推导了各自由度对残余能量贡献的表达式，通过计算故障发生后每一自由度对残余能量的贡献识别故障位置。刘文峰等［9］提出了广义应变比能概念，利用广义应变比能可以定位损伤，在测试数据充分的情况下可大致判断损伤程度。陈晓强等［10］利用小波包对结构损伤后的的动应变测试信号进行分解，选取合适的频段重构，再计算其提出的“平均伪比能”(APSED)与“平均伪比能变化率”(APSEDR)指标识别结构的损伤位置及损伤程度。

残余能量的灵敏度研究还未见相关文章发表。开展此项研究，对进一步完善结构动态特征灵敏度分析的基本理论意义重要，可为结构优化设计、有限元模型修正及结构损伤识别等的应用研究提供支撑，应用前景良好。

1 基于单元残余能量灵敏度的结构损伤识别方法

单元残余能量反映了结构的固有特性，当结构局部出现损伤时，将引起局部材料力学性能的变化，从而使结构动力特性发生相应的改变。残余能量是结构振型与频率的函数，能够反映结构的损伤信息。据此，本文分析了单元残余能量对结构刚度变化的灵敏度，提出了基于单元残余能量灵敏度分析的方法进行结构损伤定位与损伤程度的识别。

1.1 损伤系数

一般结构单元损伤定义为单元刚度降低，忽略质量变化。

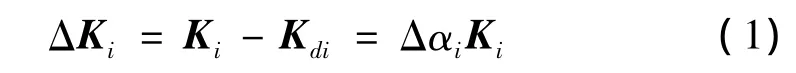
式中:ΔKi为第 i单元损伤对整体刚度矩阵贡献的减少量;Ki，Kdi为第i个单元损伤前后对整体刚度矩阵的贡献，由单元刚度矩阵扩阶后得到;Δαi为单元损伤系数，表征i单元的损伤程度。

损伤后结构整体刚度矩阵的变化可由单元刚度矩阵的改变集成得到:

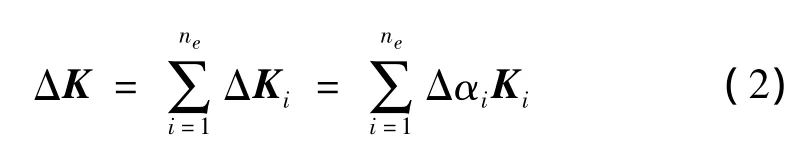
式中:Δαi∈［0，1］，当 Δαi=0，表明单元无损伤;当Δαi=1，表明单元刚度完全丧失。

单元损伤后的总体刚度矩阵为:

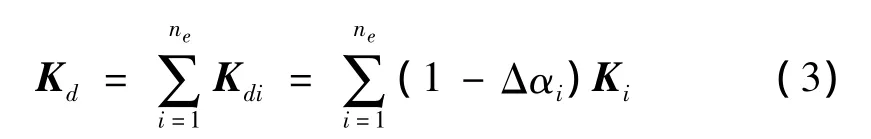
式中:ne为结构单元总数。

1.2 损伤方程组

由式(3)可知，结构损伤后的总体刚度矩阵Kd是单元损伤系数Δαi的函数，因此结构损伤后的模态参数必然是Δαi的函数，而结构的固有特性能够反应在残余能量中，因此设，对损伤后的第r阶模态参数下的j单元残余能量变化按下式作一阶变分:

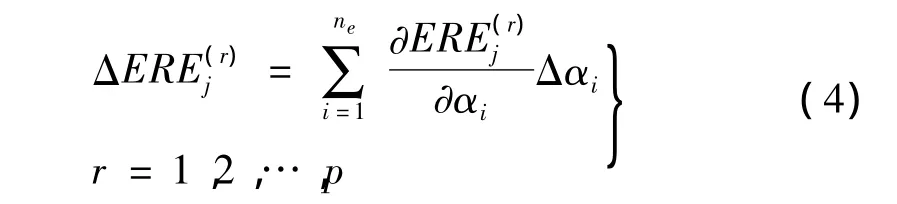
由文献［8］，对无阻尼系统，第r阶模态下j单元的残余能量定义为:

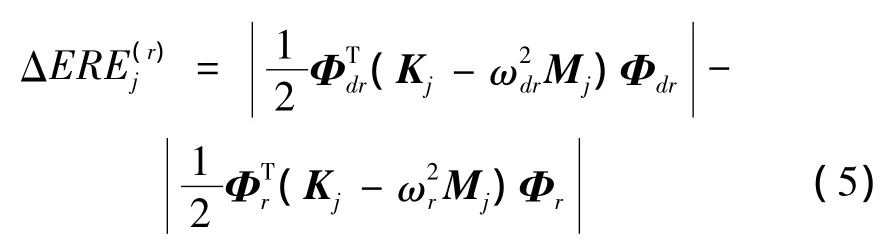
令:

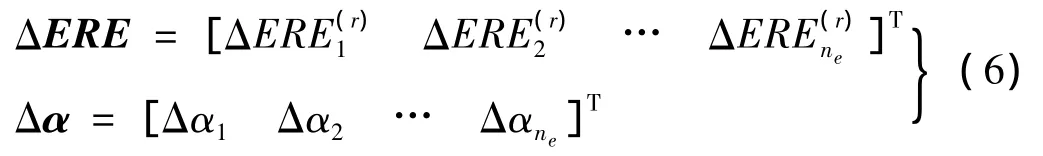
式(4)可写成矩阵形式:

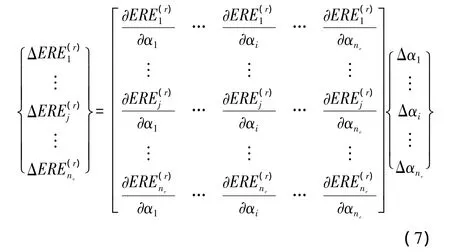
写成紧凑的矩阵形式为:

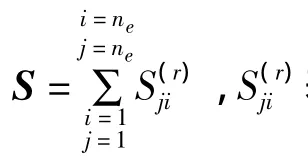
1.3 灵敏度系数矩阵构建

根据文献［11］，灵敏度系数S矩阵可由结构有限元模型计算得到，其计算过程如下:

(1)建立结构的基准有限元模型;

(2)获取未损伤结构第r阶模态频率及振型(因为低阶模态参数较易获得，一般选用第一阶模态参数);

(3)用有限元模型模拟结构损伤。令第i单元具有己知大小的损伤Δαi，其余单元无损伤，提取结构第r阶模态频率及振型，计算结构损伤后残余能量的变化量;

(5)改变i，重复以上几个步骤，最终可获得S矩阵。

1.4 损伤方程组求解

本文通过求解损伤系数向量识别损伤位置及损伤程度，由式(8)求解损伤系数向量Δα，有:

2 数值仿真研究

2.1 数值模型描述

考虑一等截面简支梁(为Euler－Bernoulli梁)，梁长 4.2 m，横截面积 A=0.075 ×0.15(m2)，惯性矩 I=2.11 ×10－5(m4)，弹性模量 E=1.495 GPa，容重 ρ=1154kg/m3。基于MATLAB平台，利用有限元方法将该梁划分为21个单元，22个节点，42个自由度。

2.2 损伤识别

图1 简支梁数值模型Fig.1 Simply supported beam mode

考虑简支梁4种损伤工况，包括单损伤及多损伤，分别记为C1、C2、C3、C4。单元损伤程度通过折减单元刚度模拟。损伤工况如表1所示。本例采用结构第一阶模态参数，利用MATLAB编程求解相应的损伤方程组，得到各工况损伤状态。损伤识别结果见表1、图2。

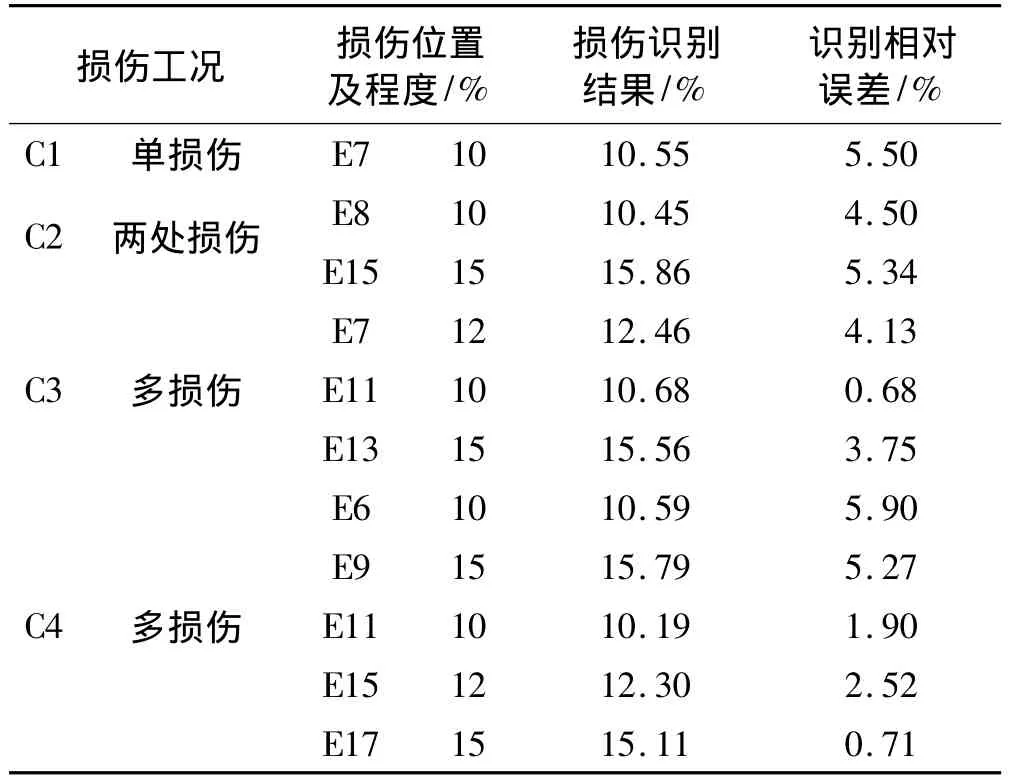
表1 简支梁损伤工况及识别结果Tab.1 Damage cases and identification results of simply supported beam

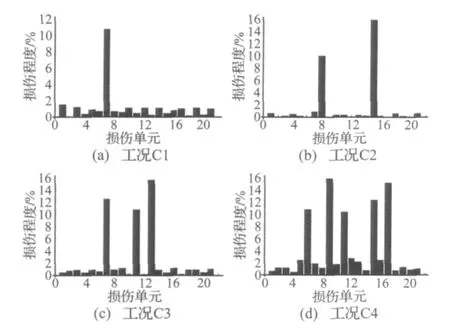
图2 损伤识别结果Fig.2 Damage identification results

由表1、图2看出，无论是单损伤还是多损伤，本文提出的方法均能有效地识别出损伤位置及损伤程度，识别精度较高，各工况下的损伤程度识别相对误差均在6%以下。

3 结论

本文在定义单元残余能量基础上进行其损伤系数灵敏度分析，提出了基于单元残余能量灵敏度分析的结构损伤识别方法，建立了结构损伤识别方程组。通过解方程，求得损伤系数向量，便可同时识别结构的损伤位置及损伤程度。仿真结果表明，本文提出的方法对各损伤工况不但能准确定位，而且能有效识别出损伤程度，损伤精度较高。因此，基于单元残余能量灵敏度的结构损伤识别方法有一定的应用前景。

［1］Saltelli A，Chan K，Scott E M.Sensitivity analysis［M］.NewYork:John WilY＆Sons，Ltd，2000.

［2］颜王吉，任伟新.基于代数算法的单元模态应变能灵敏度分析［J］.振动与冲击，2010，29(4):34 －39.

［3］Shi Z Y，Law S S，Zhang L M.Structural damage localization from modal strain energy change［J］.Journal of Sound and Vibration，1998，218(5):825 －844.

［4］Shi Z Y，Law S S，Zhang L M.Structural damage detection from modal strain energy change［J］.Journal of Engineering Mechanics，2000，126(12):1216 －1223.

［5］Alvandi A，Cremona C.A ssessment of vibration-based damage identification techniques［J］.Journal of Sound and Vibration，2006，292(1/2):179 －202.

［6］Huang T J，Liang Z，Lee G C.Structural damage detection using energy transfer ratio(ETR)［J］.Proceedings of 14th IMAC，1996:126 －132.

［7］Law S S，Shi Z Y，Zhang L M.Structural damage detection from incomplete and noisy modal test data［J］.Journal of Engineering Mechanics ASCE，1998，124(11):1280 －1288.

［8］黄方林，顾松年.用残余能量法诊断结构故障［J］.机械强度，1996，18(4):5 －8.

［9］刘文峰，柳春图.利用广义应变比能进行结构损伤识别的数值研究［J］.机械强度，2003，25(2):159－162.

［10］陈晓强，朱宏平，閤东东.基于伪比能的结构损伤识别［J］.振动与冲击，2008，27(2):29－33.

［11］王 真，程远胜.基于时间序列模型自回归系数灵敏度分析的结构损伤识别方法［J］.工程力学，2008，25(10):38－43.