陀螺系统时间有限元方法

隋永枫，高 强，钟万勰

(1.大连理工大学 工业装备结构分析国家重点实验室，大连 116023;2.杭州汽轮动力集团中央研究院 博士后科研工作站，杭州 310022;3.西安交通大学 动力工程及工程热物理博士后流动站，西安 710049)

动力学方程的时程积分是经常面对的课题，差分法数值积分是最常采用的方法［1］。在物理与力学中大量的保守体系可用Hamilton体系描述。冯康［2］指出，保守体系的差分格式应当保辛。保辛即保持保守体系结构特性。但常用的差分格式并未考虑保辛;应当指出，通常的差分格式不保辛并非错误，而是逼近真实解不够好。保辛的优点就是更好的逼近。基于变分原理的有限元是自动保辛的［3］，。根据结构力学与最优控制的模拟理论［4］，空间坐标有限元方法应用广泛［5］，它也可以用于时间坐标。事实上，Zienkiewicz［6］已提出时间坐标有限元法，但并未要求保辛。动力学有作用量变分原理，故其有限元可基于此变分原理。从变分原理导出的时间有限元矩阵也有对称性，即也是保辛的。

陀螺系统的时程积分问题可用很多方法求解，如:Runge-Kutta方法、Newmark方法及Wilson方法等，这些方法中有些只有在选取特定参数下才具有保辛特点，而以上方法均未提及保辛的内容。本文将时间有限元方法应用于陀螺系统的时程积分问题，保持了陀螺系统的结构特性，更好地逼近了陀螺系统的性态，特别对系统的长期时程分析具有很好的效果。

1 陀螺系统

如文献［4］中所述，陀螺系统拉格朗日函数为:

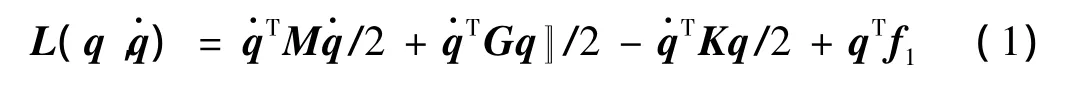
其中:q为n维广义位移向量。由此导出动力方程:

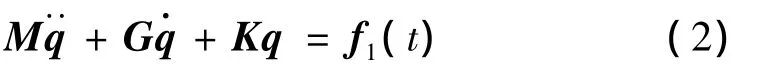
其对应的变分原理见(3)式，(4)式为对应的初值条件。

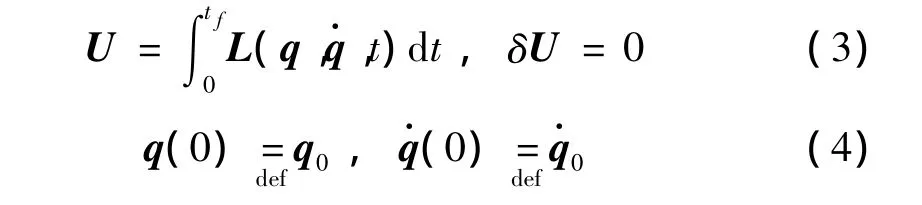
其中n×n的对称阵M，K分别为质量阵与刚度阵，G为反对称陀螺阵，此为保守系统方程。

2 陀螺系统有限元列式

图1 时间单元Fig.1 Time element

与位移有限元分析方法推导原理类似，在一时间区段(ta，tb)内(图1)的作用量函数(单元变形能)为:

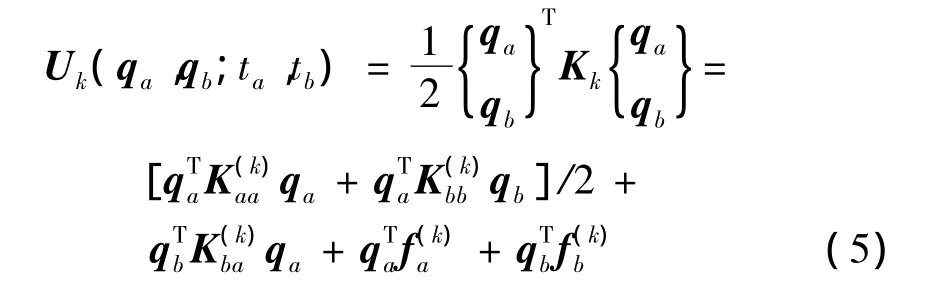
其中:

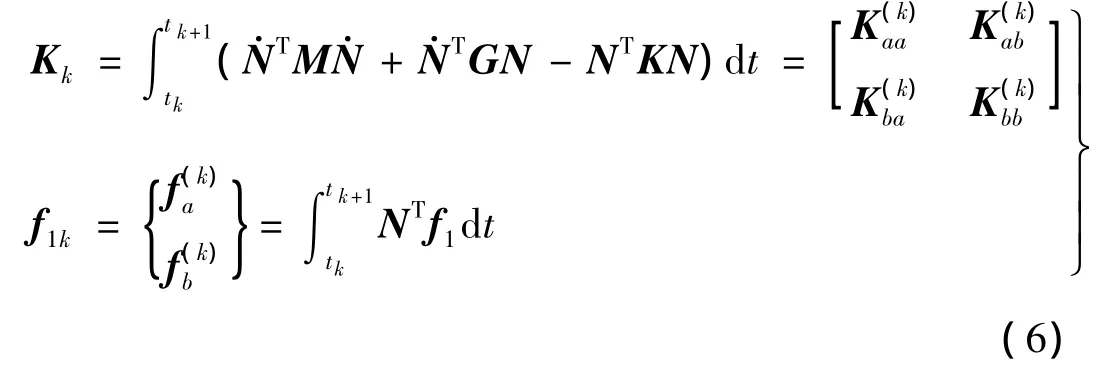
式中:Kk即为时间单元刚度阵对称阵，f1k为时间单元节点上等效外力，N为形函数矩阵。

引入动量(对偶)向量:

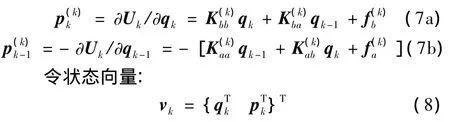
由最小作用量原理，联合式(7a)、式(7b)与式(8)可导出:

其中:

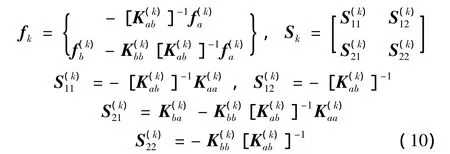
3 稳定性分析［7－8］

积分算法的稳定性只依赖于逼近算子的本征值，假定λi是n维传递矩阵S的谱半径，定义:

则当且仅当ρ(S)≤1时算法才是稳定的。

陀螺系统传递算子矩阵S的本征问题表达为:

根据辛矩阵特点及式(12)可得:

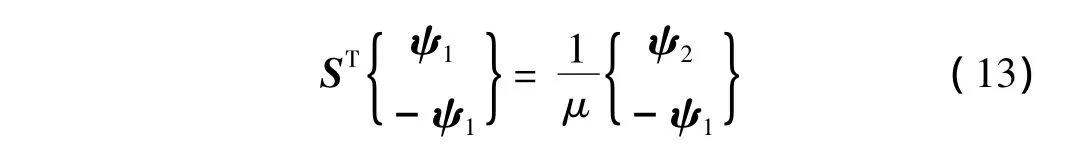
式(13)说明1/μ仍是ST的本征值，而S与ST应有相同的本征值，故知μ与其倒数1/μ必同时是辛矩阵S的本征值。

综上可知，本文算法的稳定性准则为传递辛矩阵S的谱半径必全为1。

4 形函数矩阵

在时间单元 (ta，tb)区段的进行插值，每个对应的系统自由度是相互独立的，本文各自由度的插值函数相同，即:

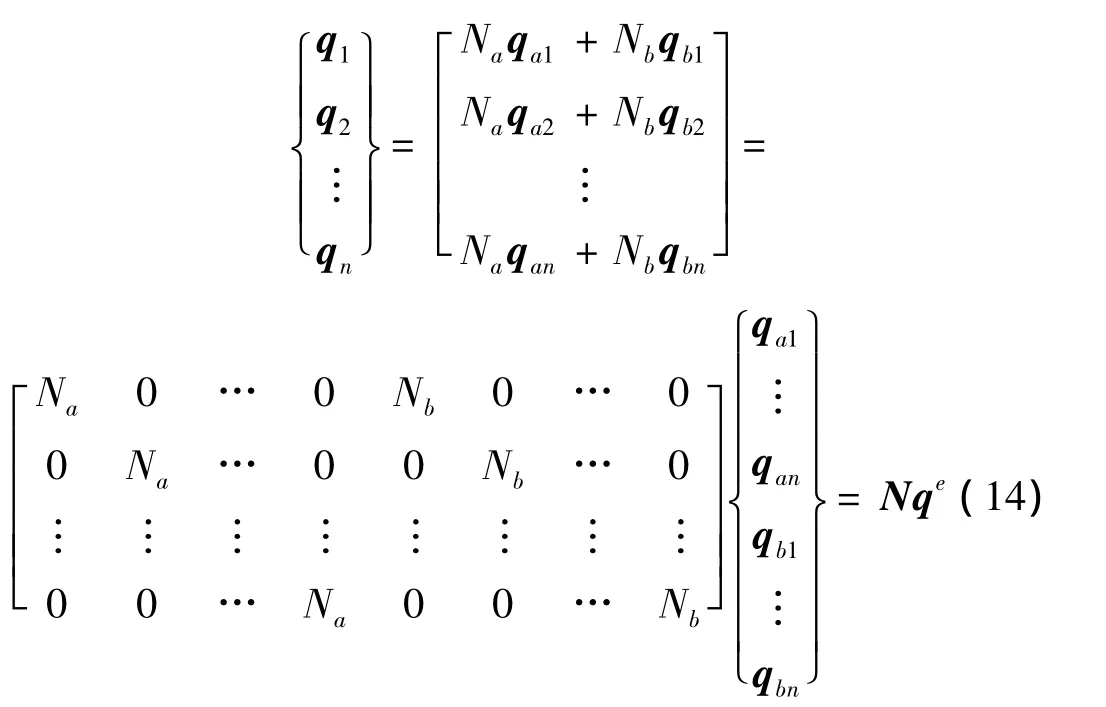
以两个自由度陀螺系统为例，讨论时域有限元形函数的选取。取一次线性时域响应模式，即一维Lagrange多项式插值，有:

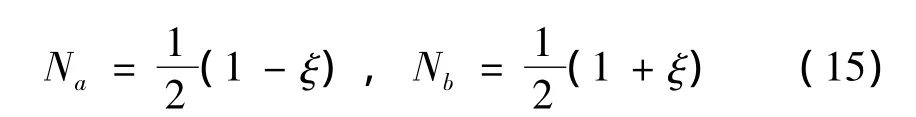
其中:

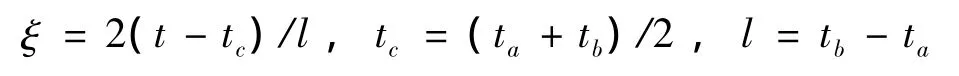
则:

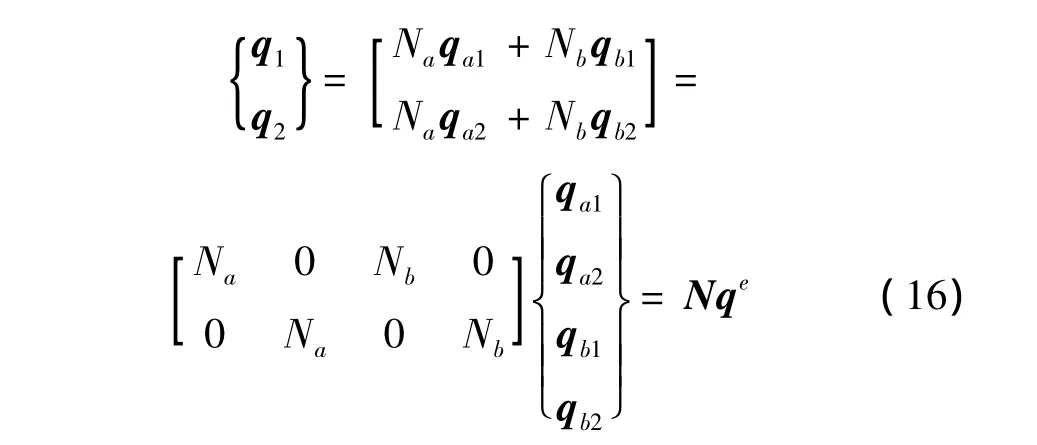
将(14)式代入(6)式可得时间单元的刚度阵:

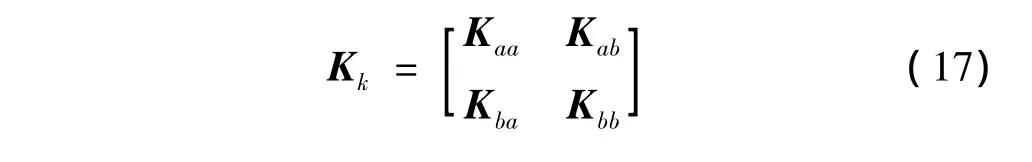
其中:

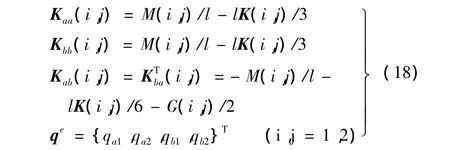
5 非齐次外力项处理

同上节，以两点线性插值形函数为例，通过(6)式计算系统的节点外力列式。如果外力f1=f0与时间无关，系统的节点外力可解析求出，对单自由度系统，外力式可表示为:

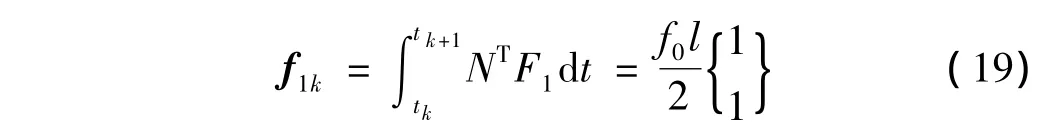
如果外力f1=f0(t)与时间有关:① 当外力f0(t)为可积分函数(如正弦，余弦，多项式和幂指数等形式)时，则节点外力列式可解析求解。② 当外力f0(t)为不可积分函数时，可用数值积分方法(如高斯积分，柯茨积分等)求解［9］。

6 例题

本节给出两自由度无阻尼自由陀螺振动系统，该方程能方便得到解析解，便于比较。

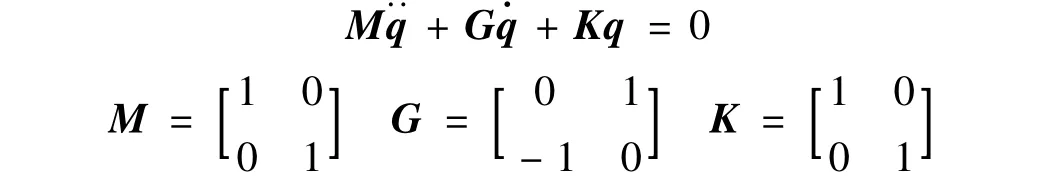
初值为:

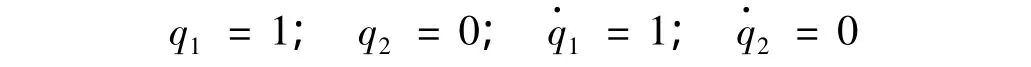
本文解析解为:

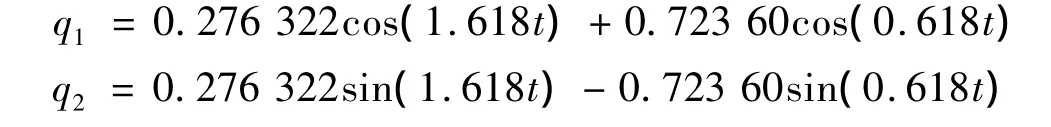
Δt=0.15 s时，可得系统时间单元刚度阵及相应的传递辛矩阵，如下。可以证明该辛矩阵本征值的模均为1，满足本文算法收敛性条件。

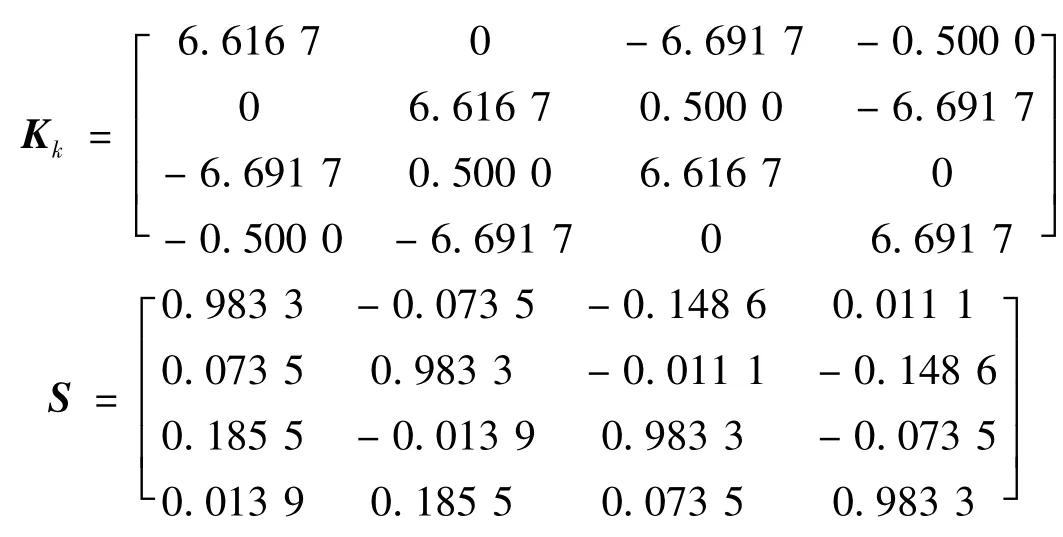
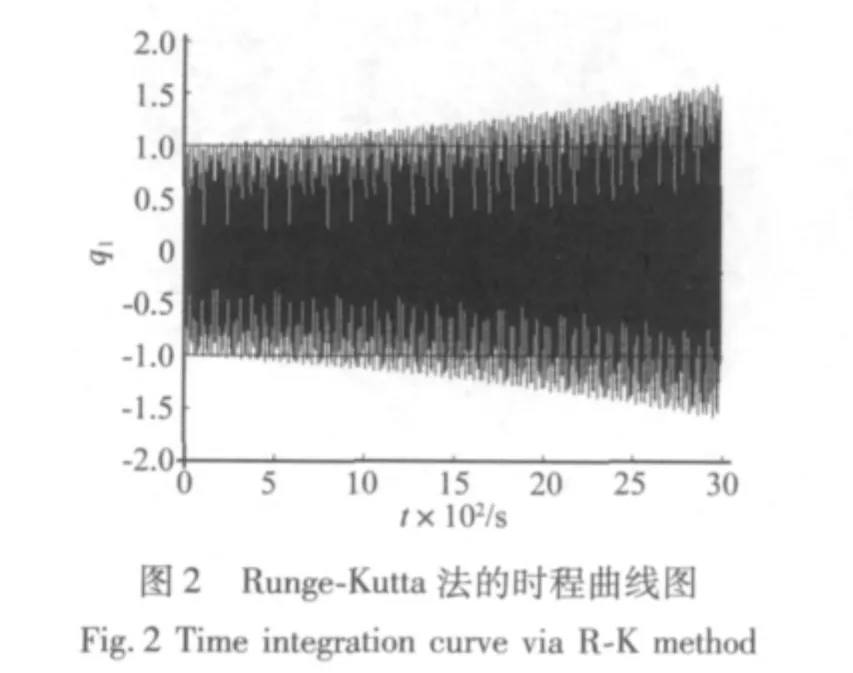
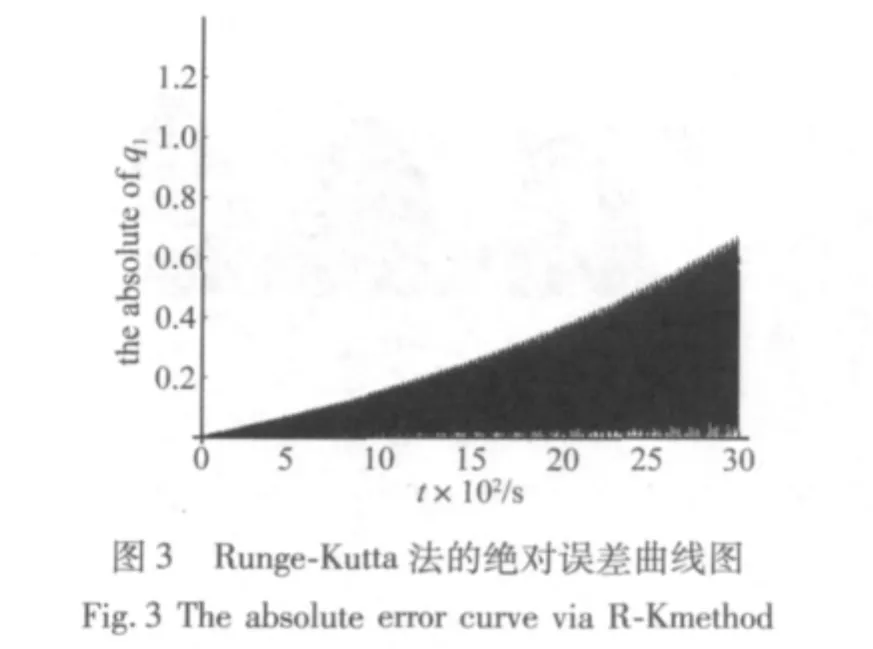
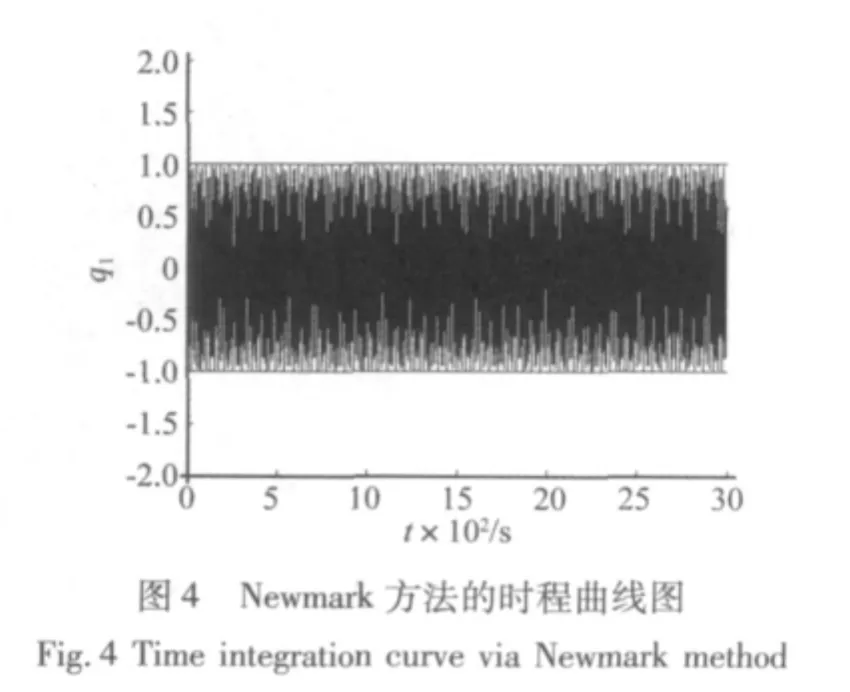
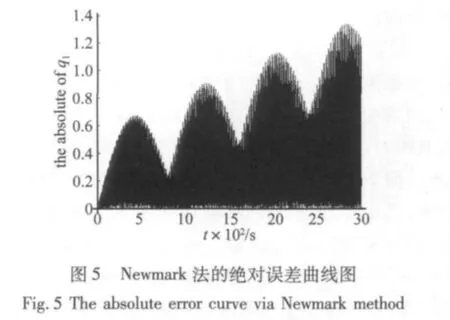
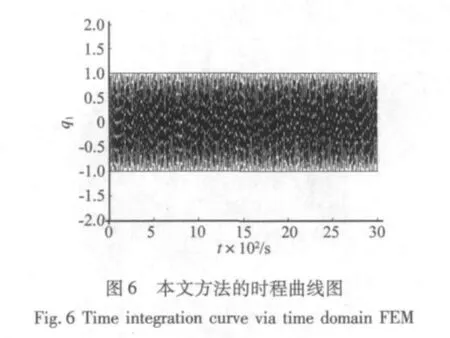
图2～图7分别为应用Runge-Kutta法、Newmark法及本节方法(TDT)求得3000 s内系统的时间历程曲线及对应的绝对误差曲线图。其中Newmark法的参数为 α =0.25，δ=0.5，图2、图4 及图6 中两横线分别为精确解的包络线。从图2和图3可以看到，Runge-Kutta法的解在积分时间过长时超出了边界，振幅是发散的，其绝对误差将发散到无穷大，算法不稳定。图4及图6表明Newmark法与本文方法(TDT)与精确解包络线吻合的很好，可知这两种方法的振幅并未发散，保证了该保守系统总体的能量守恒，算法上无耗散［2］。而图5和图7的绝对误差曲线图表明，Newmark法与本文方法(TDT)的绝对误差是由于相位的误差导致的，振幅不发散，绝对误差呈周期性扩大。在计算长时间历程曲线时本节方法的计算精度稳定，优于Newmark法。

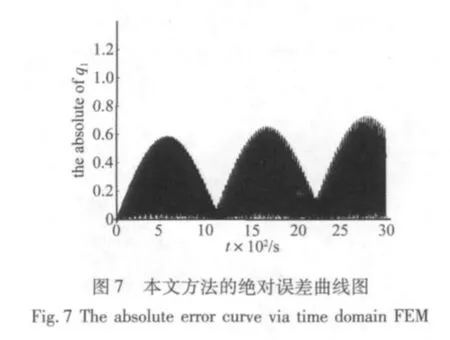
7 结论

综上所述，由于时域有限元方法是保辛的，所以无论是长期时程分析还是短期时程分析，算法都能很好地保持原系统的性态。而振幅保持不变则表明了本文算法没有产生能量耗散，虽然Newmark法的振幅也无明显变化，但其绝对误差呈相对较快速地扩大趋势，而本文方法的绝对误差呈周期性变化且在相当长的时间步长内无明显扩大。通过算例证明，在同等条件下，本文方法的计算精度高于Runge-Kutta法、Newmark法，具有很好的应用前景。

［1］Press W H，Teukolsky S A，Vetterling W T，et al.Numerical recipes in c［M］.Cambridge Univ.Press，1992.

［2］冯 康，秦孟兆.Hamilton体系的辛计算格式［M］.杭州:浙江科技出版社，2004.

［3］钟万勰.分析结构力学与有限元［J］.动力学与控制学报，2004，2(4):1 －8.

［4］钟万勰.应用力学对偶体系［M］.北京:科学出版社，2002.

［5］Oden J T，Belytschko T，Babuska I，et al.Research directions in computational mechanics［J］.Comput. Methods Appl.Mech.Engrg，2003，192(7 －8):913 －922.

［6］Zienkiewicz O C，Taylor R.The finite element method.5-th ed［M］.NY:McGraw-Hill，2000.

［7］Bathe K J，Wilson E L.Numerical methods in finite element analysis［M］.Prentice-Hall，Inc.，1976.

［8］Richtmyer R D，Morton K W.Difference methods for intialvalue problems(2nd Edition)［M］.New York:John Wiley and Sons ，1967.

［9］隋永枫.转子动力学的求解辛体系及其数值计算方法［D］.大连:大连理工大学，2006.