不等线间距铁路桥梁曲线布置新方法

(北京铁路局天津工程项目管理局，天津 300241)

1 双线铁路桥梁曲线布置方法

铁路桥梁位于曲线上时，为了使梁上受力接近均衡，一般对于梁与梁，梁与台按折线布置，是采用将梁中心线设在1/2中矢或曲线相切的曲线布置方法。双线桥梁在曲线上布置时，通常以一线按单线桥梁在曲线上的布置方法进行，故单线桥的曲线布置方法和原则也适用于双线桥梁。

双线桥梁的曲线布置根据不同的条件，通常采用以下两种方法:

1)扇形布置法。同跨各线梁的纵向中心线互相平行，各墩横向中心线及桥台挡碴前墙线，与相邻梁跨纵向中心线的交角平分线及桥台挡碴前墙线一致，呈扇形布置。扇形布置方法的优点是设计简单，施工方便，但受到适用于全桥线间距相等条件的限制。

2)平行布置法。各跨各线梁的纵向中心线不是互相平行，各桥墩横向中心线及桥台挡碴前墙皆平行于基准线(即中墩计算线，为相邻两梁跨交角平分线或特定的某一方向)，使各墩横向中心线形成平行布置。当两线线间距变化较大或线间距虽然相同，但桥梁所在曲线的半径较小时，可采用这种方法进行曲线布置，但平行布置方法的不足使设计和施工均较复杂。

2 不等线间距铁路桥梁曲线布置新方法

笔者在进行津秦沈铁路电气化改造施工图设计时曾遇到过不等线间距曲线布置的情况，鉴于双线桥采用扇形布置法或是采用平行布置法的曲线布置均不同程度存在这样和那样的问题，于是结合工程实际摸索出一套不等线间距铁路桥梁曲线布置新方法。

2.1 基本思路

在布置线间距不同的弯道时，笔者采用的方法的基本思路是把内外两条曲线当作两条单线，分别进行曲线布置，在交点距满足其最小梁缝要求的条件下，再通过两线桥墩台处交点横向连线和拨角来确定两线的相对位置。

曲线布置新方法基于双线桥墩的情况，如果两线间距变化很大，超出双线墩的常规宽度范围，采用两个单线桥墩的基础平面位置若重叠而设计考虑设置共用基础时，也可用本文介绍的新方法进行桥梁曲线布置。至于共用基础的横向中心线的位置，可通过两线的横向交点距和其与曲线的夹角确定。

2.2 计算的步骤(左线在外侧的情况)

1)先把内侧线(右线)按实际曲线资料推算实际里程。2)确定一控制墩台里程后，内侧线(右线)按单线进行曲线布置，计算出其满足梁缝要求的最小交点距、偏距和偏角。3)将求得的内侧线(右线)的桥墩横向中心线与外侧线(左线)相交，求出连线在内外侧曲线间的距离(即从内侧线计算的线间距)和外侧线各段的曲线长和各交点的相应里程。4)最后由外侧线的各交点距，单独进行曲线布置，分别求出其偏距、偏角。

施工放线时，可先把内外侧两曲线按两单线实际放出，再从右线按图纸上所示计算线间距(从内侧线计算)校核左线交点位置，确认无误后即可施工。

3 与扇形布置法的比较

扇形布置的计算规则是一律以现场定桩的左线为计算线，右线布置无论在左线的内侧还是外侧，均系根据左线按线间距推得。当左线在内侧时，先进行左线曲线布置，再通过线间距求得右线。当左线在外侧时，要先右线估算最小梁缝增值根据线间距推算到左线，然后正式计算左线的曲线布置，计算偏角、偏距和交点距，最后根据线间距再计算到右线。

用扇形法进行不等线间距曲线布置有着很多缺陷和不便:

1)计算另一条线的梁缝增值及核算梁缝增值时需考虑的线间距影响而增大或减小时，由于两条曲线不是平行线，当两线间距变化较大时，不是简单的几何关系，计算起来非常麻烦。

2)当左线在外侧时的计算，由于两次采用的线间距的标准是不统一的，直接导致的后果是初算右线(内侧线)最小梁缝是满足规定值的，可是通过左线(外侧计算线)再次计算的右线最小梁缝值可能就要比初算时的小了，当线间距变化较大时，可能导致最后计算的右线梁缝为负值，这样还需通过调整交点距离后进行复算，非常麻烦，也很容易出错。

所以当线间距不等时，尤其当左线(计算线)在外侧时，笔者认为不适宜采用扇形布置法。

笔者采用的新方法类似扇形布置，但都是以内侧线为计算线(不管内侧线为左线还是右线)，内侧线切线的垂直线来确定线间距。当左线为内侧线时，原理和扇形布置的原理是一样的。当右线为内侧线时，由于右线系线路纸上定线，且又无具体位置，存在内业断链，作为计算线时需重新推算实际里程，施工时也要实际放出该桥范围内的曲线位置。

笔者认为新方法较之扇形布置法的主要优点在于:

1)通过内侧线交点距和线间距即可求得外侧线的交点距，避免了扇形布置通过梁缝增值和线间距来求外侧线梁缝增值后再复算内线梁缝的繁琐;2)内侧线求得的交点距只要满足规定值，那通过线间距求得的外侧线交点距就更加满足规定值了，避免了扇形布置由于出现负梁缝而需要进行复算的不便。

4 与平行布置法的比较

平行布置的原理是各桥墩横向中心线及桥台挡碴前墙都平行于基准线(即中墩计算线，为相邻两梁跨交角平分线或特定的某一方向)，使各墩横向中心线形成平行布置。各墩横向中心线及桥台挡碴前墙线分别与各线两梁跨纵向中心线交角平分线之夹角β成不等角，β角与桥孔数有关，孔数越多，距离基准线越远的墩台β值越大，这样会导致墩身截面尺寸需要加大，墩台需要特殊设计，使设计和施工均变得非常复杂，如图1所示。

图1 平行布置法

笔者采用的新方法，内侧线的各墩横向中心线及桥台挡碴前墙线与各线两梁跨纵向中心线交角平分线为重合的一条线，没有β角的出现，故最后计算出的交点距在满足规定值的条件下要小于平行布置方法计算的交点距，特别在孔数多的时候，不存在需要加大墩身截面尺寸的情况，如图2所示。

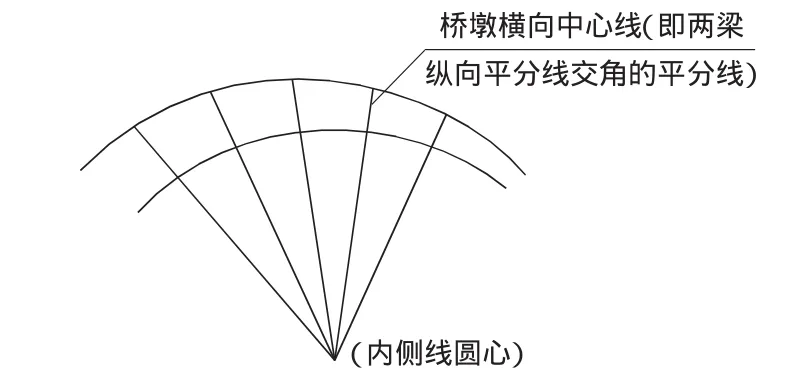
图2 新方法

5 实例分析

某6-16 m低高度先张法预应力混凝土梁羊肠河大桥，全桥位于缓和曲线和直线上，双线线间距从小里程台尾处4.8 m左右向大里程台尾处4.5 m左右变化。

5.1 计算资料

不等线间距双线桥，内侧线为右线，外侧线为左线(现场定桩线)，曲线左偏，纵断面均为平坡。

右线曲线半径R=3000 m，缓和曲线ls=100 m，曲线长L=321.53;ZH 点里程:K144+915.10，HZ 里程:K145+237.21;左线曲线半径R=3000 m，缓和曲线ls=100 m，曲线长L=334.86;ZH点里程:K144+834.84，HZ 里程:K145+237.21。

线路专业提供线间距见表1。

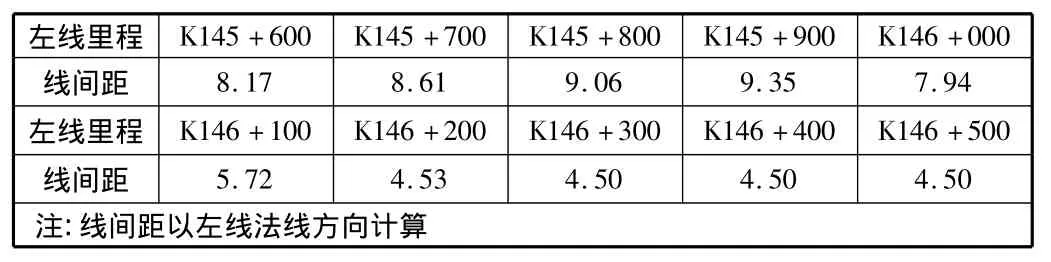
表1 线间距表

5.2 桥跨布置

5.15 m(小里程桥台)+6 ×16 m+5.15 m(大里程桥台)，控制墩台为5号墩，左线里程:K145+237.92。

5.3 计算步骤

1)计算右线实际里程。因为左右线缓直点里程相同，且线间距都为4.5 m，表明缓直点后两线直线段为平行线，故此里程都是一一对应的。因为直线上没有内业短链，故右线缓直点即为右线实际里程，可以从缓直点往小里程方向的直缓点推算。

可认为右线HZ里程为K145+237.21=右K145+237.21，右线 ZH 里程为(右 K145+237.21)－321.53=右 K144+915.68。

2)右线先按单线桥在曲线上的布置方法进行，控制墩为5号墩，因为位于直线上故里程为右K145+237.92(与左线对应)。

右线单线布置具体计算可按常规曲线布置进行，这里不再详述。

算得右线第1孔～第6孔梁满足最小梁缝要求的最小交点距分别为:16.60 m，16.56 m，16.56 m，16.56 m，16.56 m，16.56 m。

3)在右线各交点处作曲线的法线，与外侧曲线相交，求出两线横向交点距(即从内侧计算的线间距)和在左线上的对应里程。此项计算可通过编制相关电算程序求得，也可在CAD图中实际放线来求得(具体计算原理，由于篇幅有限不再赘述)。

4)最后，在确定左线各梁跨最小梁缝规定的交点距条件下，再计算出左线相应的偏距和偏角，曲线布置结果如图3所示。

图3 羊肠河大桥曲线布置图

6 结语

本文采用把内外两条曲线当作两条单线，分别布置，在交点距满足其最小梁缝要求的条件下，再通过两线间距和拨角来连接两线的相对关系的不等线间距曲线布置的新方法，适用范围广，灵活、简捷、方便，在双线铁路、多线铁路和增二线铁路桥梁曲线布置设计中具有很好的实用价值。

［1］铁道第三勘察设计院.桥梁设计通用资料［M］.北京:中国铁道出版社，1994.

［2］TB 10002.1-2005，铁路桥涵设计基本规范［S］.