一类广义Radon变换的反演*

蔡 洋，王金平

(宁波大学理学院，浙江 宁波 315211)

X射线计算机断层成像技术(X-ray CT)，作为一种重要的医学诊断手段和新型的无损检测技术， 由于其独特的成像优势，在医学和工业领域发挥着越来越大的作用，已成为医学和工业界诊断检测的主流技术之一。Radon 正逆变换对公式是 CT 重建最基础的数学理论， 不论是从医学诊断、图象处理和信号分析诸领域的实际应用还是从数学理论研究等方面,这一领域取得了丰富的成果,特别如Natterer F,Davison M,Bortfeld T和 Oelfke U等[1-7]。具体地，他们利用算子的奇异值分解理论，得到了Radon变换的反演公式，值域性质。近年来，针对不同的系统几何配置，研究者已提出多种重建算法[8- 9]。从重建方式而言， 可以把这些算法分为基于逆求解公式(Inverse formula)的解析法如Novikov R和基于统计模型的迭代法两类[10-12]。解析算法主要通过对成像模型进行分析，获得其相应的数学求逆公式来实现，具有实现简单、运算速度快的优点。单光子计算机断层成像(SPECT)是核医学的一种非侵入的诊断技术，投影数据用数学表达式刻画就是著名的衰减Radon变换。

相应地，图像重建就是求其逆变换，FBP-型反演公式分别由 Novikov R和 Natterer F得到。 广义Radon变换是Radon变换的推广和多种情形的表示，衰减Radon变换是其一种情形之一(见文[13-14])。 作为一个线性算子，广义Radon变换是通过某种特殊的测度，以在超平面上的积分的形式作用于n维欧几里得空间上的函数上。在此文中，我们记ω为单位球面Sn-1上的一个点， 即ω∈Sn-1，再有s∈R1，广义Radon变换定义为

(1)

此处 Φ(x,ω) 为(1-2)μ,这里 <,>表示Rn上的点积。当μ=0 时，(1)式即为Radon变换。

下面引入标准的奇异值分解方法：

假设R是从希尔伯特空间H到K的连续线性算子，并且RR*:K→K有一个完全的特征函数系gi,i=1,2,…,与之相联系的特征值系为λi,i=1,2,…,且λi>0。 若令

,i=1,2,…

(2)

Hgi

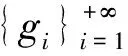
(3)

这里 <,>H表示H上的内积。同样对于给定的g∈K,‖Rf1-g‖的最小范数解f1可由下式得到

(4)

Φ(x,ω)=(1-2)μ,H=L2(Ωn,Wn),

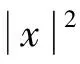
1 辅助结论及相关引理

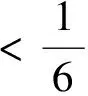
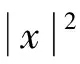
H→L2(Sn-1×[-1,1],(1-s2)μ-n/2)=K

(5)

是连续线性算子。

证明因为

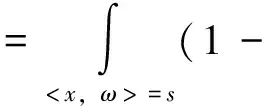
故得到

进一步有

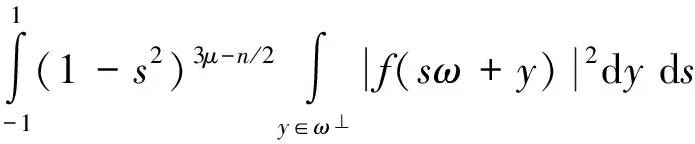
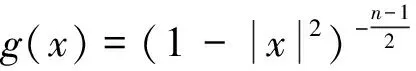
≤C1‖f‖Wn‖g‖≤+∞

于是可得结论，证毕。

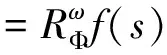
·Bω(gW1)(x)

(6)

其中Bω是满足下式的背投影算子

(Bωg)(x)=g()(1-2)μ

(7)

我们有以下算子

∶L2(Ωn,Wn)→L2([-1,1],W1),

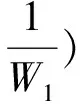
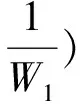
这里IWn表示点乘Wn，“*”表示算子的共轭。易证IWn与IW1是希尔伯特空间上的同构算子，因此从上面这些算子可以得出

·Bω·IW1

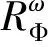
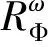
ω

(8)

其中Gω(s)=G(ω,s)，s∈[-1,1],ω∈Sn-1,x∈Ωn。则RΦ是从H到K的连续线性算子。

证明对于∀f∈L2(Ωn,Wn)，那么

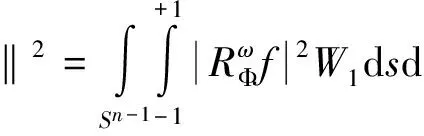
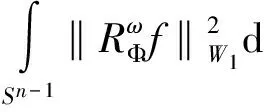
即说明RΦ是H→K的有界线性算子，由于H和K均为希尔伯特空间，从而RΦ是H→K的线性连续算子。而根据共轭算子的定义(8)式很容易得到。

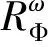
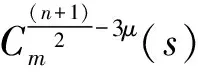
通过坐标的旋转我们可仅需考虑ξ=(1,0,…,0),ω=(cosθ,sinθ,0,…,0)时的情况，由(6)，(7)式得到

因此

(ξ,s)=

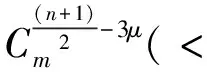
这里利用了

参看文[1]。

引理5 对m=0,1,…，令Vm是引理1中所述K的子空间，且Vm中元素有形式G(ω)Tm(s),这里G(ω)∈L2(Sn-1) 则有

(i){Vm}构成了K的正交子空间系；

(iii)

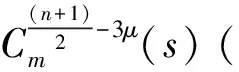
对于(ii)，(iii)，令G(ω)Tm(s)∈Vm，则

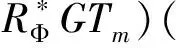
后一等号由引理4得到。

2 主要结论及定理

证明由[1]知，Funk-Hecke定理可表述如下：

对于[-1,1]上的连续函数F(t)，成立

<ξ,ω>)Yl(ξ)dξ=

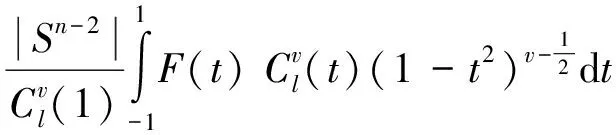
由Funk-Hecke定理及引理5中的结论有

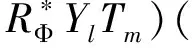
λlmTm(s)Yl(ω)

证毕。

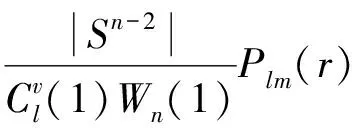
其中

Plm(r)=rlqml(r2)=

qml(r)是关于r的最高阶为m-l的多项式。

证明直接计算得

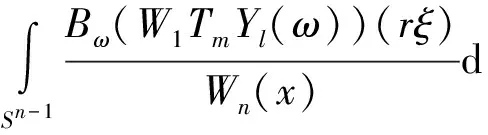
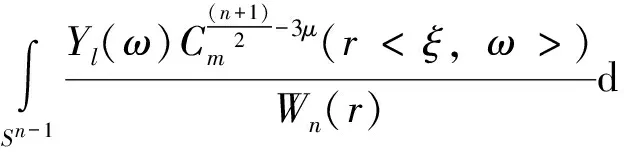
利用Funk-Hecke定理得到原积分为

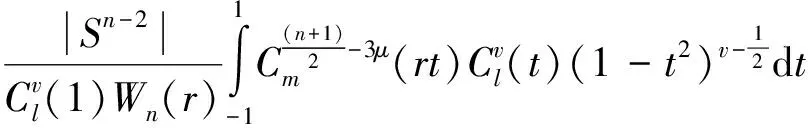
我们记

和

则下式成立：

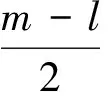
进一步作代换u=r2，得到

,

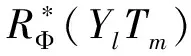
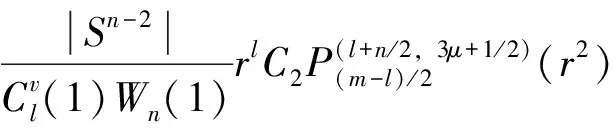
为了方便，记

glmk(ω,s)=Tm(s)Ylk(ω),

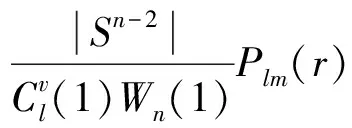
这里Nn-1(l)为n维球面调和函数空间中阶为l的球面函数的个数。从而根据标准的奇异值分解法，对于∀f∈L2(Ωn,Wn),有

这样就可以根据要求采用截断方法得到对图像函数的一种逼近和近似重建。

参考文献：

[1]NATTERER F.The mathematics of computerized tomography [M].Reprint of the 1986 original.Classics in Applied Mathematics,32.SIAM,Philadelphia,PA,2001.

[2]NATTERER F.Inversion of the attenuated Radon transform [J].Inverse Problems,2001,17(1): 113-119.

[3]DAVISON M.A singular value decomposition for the Radon transform inn-dimensional Euclidean space [J].Numer Funct Anal Optimiz,1981,3: 321-340.

[4]BORTFELD T,OELFKE U.Fast and exact 2D image reconstruction by means of Chebyshev decomposition and backprojection [J].Phys Med Biol,1999,44: 1105-1120.

[5]MAASS P.The x-ray transform: singular value decomposition and resolution [J].Inverse Problems,1987,3: 729-741.

[6]WANG J P,DU J Y.A note on singular value decomposition for Radon transform inRn[J].Acta Mathematica Scientia,2002,22B (3): 311-318.

[7]胡良根.渐近半压缩映象的收敛性定理[J].宁波大学学报: 理工版,2008,21(4): 514-519.

[8]XIAN J,LI S.General A-P iterative algorithm in shift-invariant spaces [J].Acta Math Sinica,English series,2009,25(4): 545-552.

[9]XIAN J.Weighted sampling and reconstruction in weighted reproducing kernel spaces [J].J Math Anal Appl,2010,367(1): 34-42.

[10]NOVIKOV R.An inversion formula for the attenuated X-ray transformation [J].Ark Mat,2002,40: 145-167.

[11]LI T,WEN J,HAN G,et al.Evaluation of an efficient compensation method for quantitative fan-beam brain SPECT reconstruction [J].IEEE Trans Med Imaging， 2005,24(2): 170-179.

[12]FINCH D.The attenuated x-ray transform: recent developments,in inside out: Inverse problems and applications [C]∥MSRI Publications,47,Cambridge Univ.Press,Cambridge,2003,47-66.

[13]XU Y,TISCHENKO O,HOESCHEN C.Approximation and reconstruction from attenuated Radon projections [J].SIAM Journal on Numerical Analysis,2007,45: 108-132.

[14] XU Y.A new approach to the reconstruction of images from Radon projections [J].Adv Appl Math,2006,36: 388-420.