船闸阻抗影响下的内河航线非线性配船模型

林珈伊，陶桂兰

(河海大学港口海岸与近海工程学院，南京 210098)

0 引言

航线配船主要是解决多型船在多条航线上的合理配置问题.不同类型的船舶放在同一航线上营运，其经济效益不同，同一类型的船舶在不同航线上营运，其经济效益也不同.对于一个经营大范围多条航线运输的大型航运企业，船队中往往拥有多种类型的船舶(如不同尺度、不同吨级、不同航速等).如何将这些船分配在自然条件不同的多条航线上运行，使船队总利润最大化，是一个复杂的问题.

目前，航运企业使用的航线配船方法主要是线性规划法［1］，通过现有的特定运算程序用计算机求解，能方便快速地得到最优航线配船方案.但是，有学者发现，在航道和港口日益繁忙的情况下，将原问题简化为单纯的线性模型，即假定船舶每航次所需时间为常数而将年货运成本和运量固定下来，所得的结果往往偏离实际，有必要考虑建立受航次时间变动影响的非线性配船模型.［2］基于此，本文研究内河航道上因船闸服务能力限制造成的船舶航次时间延误情况［3］，即船闸处的时间阻抗变动，并建立船闸阻抗影响下的内河航线非线性配船模型.

1 船闸阻抗分析

航道上修建船闸后，会影响船舶的航行时间，因为船闸的通过能力会限制单位时间的过船量.在内河运输需求不断增长的今天，很多船闸的服务水平已达到饱和，所以每一艘船经过船闸的总时间阻抗不仅包括一次过闸时间，还应考虑过闸前的排队待闸时间，这一时间可用排队论理论求解.

船闸的一次过闸时间

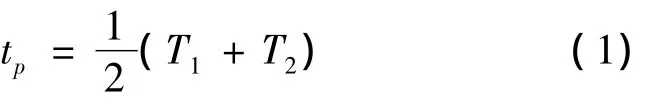
式中:T1为单向一次过闸时间，T2为双向一次过闸时间.T1和T2均由开闸门和关闸门时间、单向(或双向)进闸和出闸时间、闸室灌水和泄水时间以及船舶进闸和出闸的间隔时间组成.

排队待闸时间与已到船舶数量有关，所以需要先确定船闸单位时间到船量的概率分布情况.在船闸实际运行中，船舶到达通常是随机的，根据京杭运河施桥船闸到船概率分布统计资料［4］可以看出，某一到船艘数分组内到船艘数出现的频率比较小，描绘这种概率的数学模型通常采用泊松分布(因为与船闸到船情况类似的港口到船和道路上的车辆数的概率服从泊松分布).如果用n表示单位时间内到达的船舶数，则船闸到船概率

式中:λ为单位时间内船舶的平均到达率.通常，船闸上行和下行船舶的到达情况不同，应分别统计到船概率.

待闸时间不仅受到船率的影响，还与船闸服务时间有关.船舶过闸的服务程序一般有远程申报、过闸收费、联合调度、安排过闸等4项.根据对施桥船闸和淮安船闸的过闸服务时间频率分布统计资料［5］分析可知，虽然每艘船的过闸服务时间不同，但大多集中在某一时间区段内，只在某一均值时间左右波动，故可认为其服从一般分布.根据船闸的统计资料，可由概率论理论确定船闸服务时间的期望值 E［T］和方差 Var［T］.

在上述条件下建立的排队论模型为M/G/1模型，平均排队队长用下式［6］计算:

式中:ρ为服务强度，ρ=λ·E［T］＜1，则平均待闸时间为

一艘船经过船闸处的总时间阻抗

由式(5)可见，t是λ的函数.λ与航线上其他船队的运输船数量及本船队分配在该航线上运营的船舶数量有关，数量越多，船闸处排队等候时间越长，单船每航次的经济效益就越低.

2 建立航线配船模型

结合以上船闸交通阻抗分析可知，在λ已知的情况下可计算出t，根据船舶在船闸段以外的航道行驶时间和港口逗留时间可得每航次时间.这是建立非线性航线配船模型的基础.

2.1 航线配船的线性规划模型

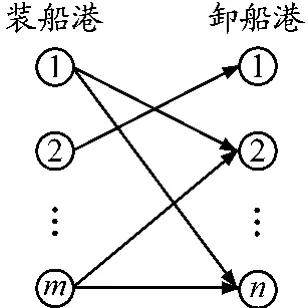
图1 船队运输网络

先假定某航运公司船队运输线路，见图1.承担运输任务的航区由若干个装船港和若干个卸船港组成，它们之间由G条航线相连.假定船舶都以简单的航次形式运货，船队现有K种类型的船舶.航线配船的规划即考虑G条航线上K种船舶的调配使用.同时，船队也必须完成各条航线上的货运任务.

根据以上条件，以船队年营运总费用最低为目标，年营运总费用z与分配在各条航线上运行的各种类型船舶数量xjh和闲置的各种类型船舶数量O之间的关系(即目标函数)为

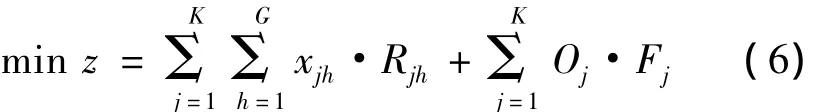
约束条件有

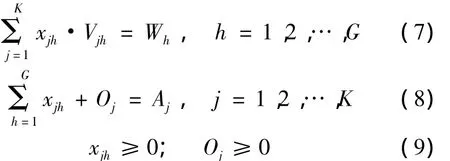
式中:z为目标函数，即年度营运总费用;xjh为决策变量，即在h航线上配置的j型船的数量;Oj为决策变量，闲置的j型船数量;Rjh为j型船在h航线上的单船年营运费用;Fj为j型船闲置一年的费用;V为j型船配在h航线上营运时的单船年运量;Wh为h航线上应完成的年运量;Aj为船队中拥有的j型船的数量;K为船型总数;G为航线总数.

2.2 非线性因素影响的航线配船模型

上述线性规划模型中的Rjh和Vjh是与xjh取值大小无关的常数，求解十分方便，然而在实际情况中Rjh和Vjh很可能与xjh相关.如前所述，对于内河航道而言，航道中通常建有若干座船闸等通航建筑物，当航线上的船舶过多时，船舶过闸往往需要排队等候，船舶数量越多，排队时间越长，航次时间也越长，这将导致单船年营运费用Rjh和年运输量Vjh随之变化.也就是说，从整个系统考虑，当航线上运营的船舶数量较多时，船舶的年营运费用和年运输量都是航次时间的函数，航次时间除了与航道里程相关外，还与船舶在船闸、港口以及其他不利于畅通行驶航段的排队等候时间长短有关，从而影响最优的配船方案.下面建立船闸处时间阻抗影响下的非线性航线配船模型.

j型船在h航线上营运的平均航次时间

式中:t1jh为h航道上j型船除去船闸段的航行时间，即船舶以自由航速航行的时间;tijh为j型船在h航道上第i座船闸处消耗的时间，可由式(5)确定;t2jh为j型船在该航线的装船港和卸船港逗留的时间(应与港口的泊位占用率有关，若到港船舶数量较多而泊位数较少时，同样也要考虑非线性影响［2］，但本文将其看作一定值，主要考虑航道上的船闸阻抗带来的非线性影响).

前文中计算船闸交通阻抗时要先确定λ，不同航线上船舶的到达与否是相互独立的，而某条航线某船闸处总的平均到达率应是该航线所有船舶到达率之和，即

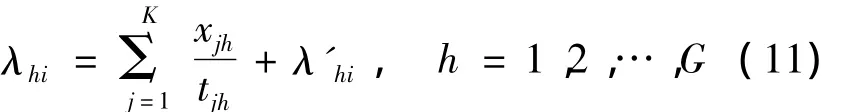
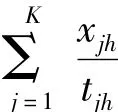
根据航次时间可得j型船在h航线上营运的年航次数

式中:Djh为j型船在h航线上的年营运时间.于是，在h航线上j型船的单船年营运成本

式中:RC，jh为j型船在h航线上营运的航次平均成本［7］;R'C，jh为与在船闸处停留时间长短无关的航次费用(如燃润料费、按挂靠次数征收的港务费、维修费、保险费、税费等);R″C，jh为与在船闸处停留时间长短有关的航次费用(如船员工资、管理费、日常开支等)，它是 tjh的函数，可表示为 R″C，jh=tjh·R‴C，jh.

在h航线上营运的j型船的单船年货运量

式中:VC，jh为j型船在h航线上营运的航次平均货运量.

可见，Rjh和Vjh都是 tjh的函数，也是xjh的函数，计算时可用迭代法求解.具体步骤如下:

(2)得计算所得的t代入式(10)，计算各型船在各条航线上的tjh，再由式(12)计算njh.

(3)再根据式(13)和(14)计算 Rjh和 Vjh，将其代入线性规划模型式(6)～(9)，可得第1次分配方案.

(4)将第1次分配结果代入式(11)右边第1项，得第2 组船队平均到达率(，，…，)，迭代m次后，若为给定误差)，则迭代终止，最后的分配方案即为最优解.

3 算例分析

图2 船队运输航线

某内河运输船队拥有500 t级和1 000 t级的运煤单船各20艘，用这些船承担运输任务的航线系统由连接一个装煤港A和两个卸煤港B1和B2的两条航线组成，见图2.AB1航线上有一座船闸 D，AB2航线上有两座船闸E和F.各条航线上其他船队的船舶到达各船闸的到船率λ'hi，船闸的服务时间E［T］和方差Var［T］以及船舶一次过闸时间tp见表1(表1中的数据以京杭运河施桥船闸到船和过船的小时流量统计为参考依据［3，5］，取一些接近施桥船闸的数据作为已知值)，各船型在各条航线上的营运参数见表2.航线AB1的年运输量需求为 200万t，航线AB2的年运输量需求为180万t.

表1 各船闸已知参数

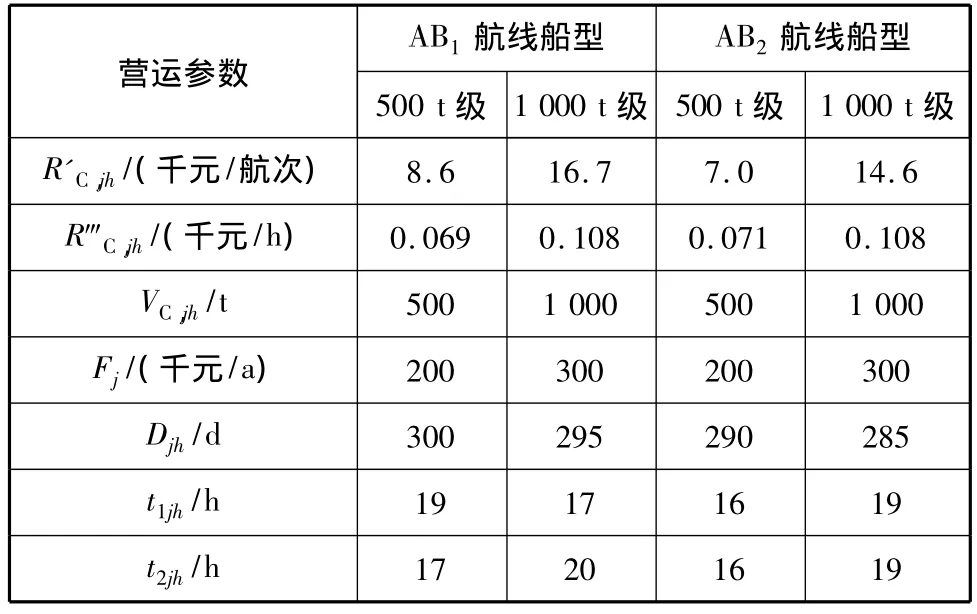
表2 已知营运参数

用MATLAB计算可得最优配船方案为:AB1航线上配15艘1 000 t级运煤船;AB2航线上配16艘500 t级运煤船和5艘1 000 t级运煤船;另外4艘500 t级运煤船闲置.

计算时假定两条航线的船队船舶初始到达率均为0.5 艘/h，即=［0.5，0.5］.经过 3 次迭代后，得到的船舶初始到达率与上一次到达率的误差已小于 0.01，即，满足精度要求;迭代8次后，误差可小于10－10.由此可见，用该模型计算本例时的迭代效率较高.迭代后得AB1航线船闸处船队船舶的到达率为0.282艘/h，AB2航线上船队船舶的到达率为0.423艘/h.

本例中，如果不考虑由于该船队在各航线上配船数量的多少所引起的各船闸处到船率的变化(即忽略本船队到达率的影响)，而将船闸处的时间阻抗作为定值，其他数据不变，则原问题就简化为年航次成本和年货运量为定值的线性规划问题.此时求得的最佳配船方案为:AB1航线上配1 000 t级船13艘;AB2航线上配500 t级船20艘，1 000 t级船3艘;其余船闲置.由此可见，用这种方法设计的分配方案与本文采用的考虑船闸处时间阻抗变动影响的非线性配船模型所得结果不同，因为它忽略本船队船舶在航线上营运后所增加的船闸处待闸时间，而本文模型考虑的因素更加全面，使计算出的年航次数、年营运成本和年货运量更接近实际情况，比单纯的线性模型更合理.

4 结束语

结合排队论理论把船舶在船闸处的待闸时间表示成到达船闸的船舶数量的函数，将航次时间作为一个随船闸时间阻抗而变的变量代入线性模型，从而建立可通过迭代求解的非线性航线配船模型.该模型考虑繁忙航线船闸处船舶由于排队等候而产生的时间延误，并从产生延误的根本原因(即过闸需求得不到满足)出发计算延误的时间长短，较真实地反映船闸处的时间阻抗，使计算所得的经济成本更合理并且接近实际可能产生的费用，而简单的线性模型则无法做到这一点.当航线上有多座船闸并且船队中待分配的同种类型船舶数量较多时，船闸处的总时间阻抗随到船量的波动会比较显著，考虑这种非线性影响十分必要.

［1］CHRISTIAN M，FAGERHOLT K，RONEN D.Ship routing and scheduling:status and perspectives［J］.Transportation Sci，2004，38(1):1－18.

［2］谢新连.船舶调度与船队规划方法［M］.北京:人民交通出版社，1997:75－86.

［3］朱俊.基于船舶流的交通时间阻抗模型［J］.武汉理工大学学报:交通科学与工程版，2010，34(3):91－594.

［4］廖鹏.京杭运河苏北段船闸通过能力研究［D］.南京:河海大学，2004:22－40.

［5］吴玲莉，张玮，廖鹏.船闸待闸时间特性分析［J］.武汉理工大学学报:交通科学与工程版，2006，30(1):99－102.

［6］孙恒荣，李建平.排队论基础［M］.北京:科学出版社，2002:116－121.

［7］赵刚，祁斌.上海电煤长江运输系统航线配船优化［J］.上海海事大学学报，2004，25(3):51－55.