船舶过闸模型的构建与应用

□ 吴嘉杨

一、船舶过闸问题描述

为了提升航道通过能力，人工制造上游调节水库，在航道上通常建设一些水利枢纽，称为船闸。船舶过闸问题即是给定船闸闸室大小，在待闸区如何选择过闸船舶从而使得待闸区中的船舶能够尽快通过大坝。

在过闸流程上进行分析基础上，船舶过闸的方式因排挡方案的不同而不同。以最为常见的最优过闸排挡方案为例，船舶过闸模型的描述如下:给定船闸闸室宽度为W，长度为L，易知 L ＞W，待闸船舶集合 S={S1，S2，L，Sm}，第 i艘船的长度为li，宽度为wi(此处船舶的长度l和宽度w均包含了横纵向安全间隔，下同)，船舶吨位为ti，船舶过闸变量zi=(1，0)，表示第i艘船是否过闸。

过闸模型目标为如何选择过闸船舶使得本次过闸的船总吨位或载货总吨位或利用率为最大值。

在此模型中，一次过闸选择的船舶是为最优配比、满足吨位最大的条件，待闸区中的某一艘船可能永远无法过闸，由此，可以以另一种思路即假设我们事先知晓了很长时间段内到来的所有船舶S={S1，S2，L，Sm}，并知晓其中任意一艘船舶Si的长度为li，宽度为wi，船舶吨位为ti。

过闸模型目标为如何选择过闸船舶使得在所有船舶都能过闸的情况下，所使用的闸次最少。

二、船舶过闸模型建立

(一)约束条件一:闸室界限约束。一般船闸闸室长度比宽度数值要大，故以船闸闸室左下顶点为原点，长宽为两条数轴建立平面直角坐标系，闸室区域可表示为RW×L，则第i艘船的左下顶点坐标在闸室坐标系中表示为(xi，yi)，在闸室内所占区域为Rwi×li。船舶停靠在闸室内必须满足船舶的四个数学顶点必须在闸室内，即:0≤xi≤xi+ziwi≤W且0≤yi≤yi+zili≤L。

(二)约束条件二:闸室界限约束。第i艘船舶内任意一点在闸室坐标系中可表示为(ui，vi)∈Rwi×li，易知对于每一艘船舶 li＞ wi，故 xi＜ ui＜ xi+ziwi且 yi＜ vi＜ yi+zili。将闸室内的每一艘船舶投影到坐标轴上，船舶之间的相对关系位置可以分为五种情况讨论，分别为第j艘船舶在第i艘船舶上方，第j艘船舶在第i艘船舶下方，第j艘船舶在第i艘船舶左方，第j艘船舶与第i艘船舶重叠。

只要排除最后一种情况，则满足船舶两两不重叠条件。即:(2xj-2xi+zjwj-ziwi)2≥(zjwj+ziwi)或(2yj-2yi+zjlj-zjlj)2≥(zjlj+zili)2。

(三)约束条件三:闸室内船舶排列列数约束。通常为了使船舶停泊在闸室内更加安全，只允许放下两列船，则可以将船舶的两边锚定到闸室的两条边上，约束条件为xi=0 or xi+ziwi=W。

由以上约束条件根据不同的目标函数，建立模型。

模型一:目标函数为总吨位最重。

为求得最优配比模型，本目标函数只考虑船舶总吨位。故过闸最优配比方案过闸模型为。Z=max∑ziti

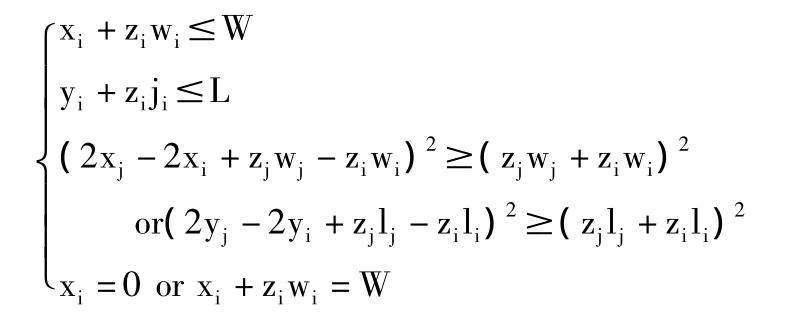
模型二:目标函数为总过闸次数最少。

对于另一种过闸模型，由于船型分布是离散的，可以根据船型，列出所需要的所有过闸模式，设共有o种，即最终需要过闸的次数为o，建立二维矩阵Bmo，对矩阵中任一元素bik(i=1，2，L，m k=1，2，L，o)的意义为第 i艘船舶是否进入第k种过闸模式，则bik=1或0。

易知任意一艘船舶至少且只能进入一种过闸模式，即∑bik=1(i=1，2，L，m)。

而对任意一个过闸模式，依然需要满足船舶两两不重叠，且船体在闸室区域内的条件，每一个过闸模式中，最多只能排两列船舶，则此模型为:min o

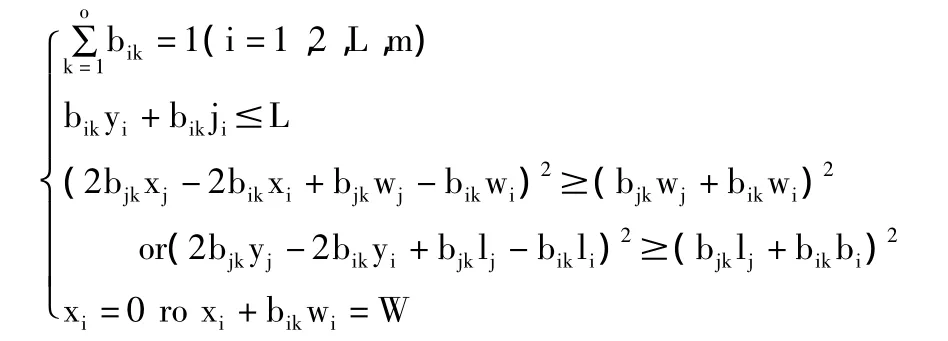
两种模型为船舶过闸问题的两种思考方向，可视为对偶模型，且均为NP-Hard模型，虽然最优解一定存在，但在二项式时间内无法找出最优解，所以模型需要用另外的方法解出，相较于二维装箱模型，船舶过闸的模型与其类似，但船舶过闸模型的目标与二维装箱模型有一定的差异，即过闸目标中加入了船舶价值系数，即船舶吨位;相较于背包模型，也有一定差异，即船舶过闸模型考虑了每一艘船的摆放位置。故本次研究中假设所有设计船型的宽度加上横向安全距离后都不大于闸室宽度的一半长，针对模型一，两列船舶排列由于互不侵占，可以对每一列进行单独计算，由此可以将这种模型转化为背包模型进行求解;针对模型二，船舶过闸模式不再是二维过闸模式，而是一维过闸模式，对模式的穷举则可以采用一维切割的穷举法列举。

三、算法介绍

(一)背包问题算法介绍。由于闸室宽度在基础资料中已经给定为定值，且此定值满足在任何情况下都可以容纳两艘任意型号船舶并排排列，而闸室内因为安全考虑最多容纳两列船舶过闸，因此可以去掉原约束条件中的所有宽度约束，原问题简化为:Z=max∑ziti∑zili≤L即为0-1背包模型。

如此，将每一艘待闸船舶看作待入背包的物品，闸室看作背包，则船舶过闸问题可以用背包问题来进行模拟。在上述对背包问题的解法当中，由于闸室长度与待闸船舶的数量均有限制，故可以采用动态规划法精确求解。

将所有待闸区n艘船舶按序排列(S1，S2，L，Sn)，则每一艘船舶Si的长度为li，载重吨位为ti，过闸系数为zi。设闸室长度为L。建立矩阵An×L，Aij的意义为将船舶序列前i艘船放入长为j的闸室当中的最大过闸重量∑zsts，cs=0，1。

对任意第i艘船来说，此次过闸只有两种情况即通过或不通过，若通过则此次过闸问题可转化为求前i-1艘船放入长为j-li的闸室当中的最大过闸重量。即Aij=Ai-1，j-li(zi=1)。

若第i艘船此次过闸不通过，则问题可转化为求前i-1艘船放入长为j的闸室当中的最大过闸重量。即Aij=Ai-1，j(zi=0)。

而此船本次过闸是否通过则取决于Ai-1，j和Ai-1，j-li+wi的大小，若Ai-1，j-li+wi大，则取此船;否则不取此船。

由此计算出的An×L矩阵后，再由后向前查找根据Aij与Ai-1，j是否相等来确定此船是否通过船闸。最后得到本次过闸吨位∑ziwi。

再根据已经确定的一次过闸时间，利用一定的概率分布条件，确定在此时间内到达船舶的吨位级别加入到本次剩余的船舶序列中，为下一次背包算法循环提供参数。

(二)线性规划算法介绍。在船队过闸问题中，由于船型组合及吨位已在基础资料中给定，要求得相对确定的闸室有效面积的最大一次过闸平均吨位，我们可以进行逆向思维，即假定有一定数量(数量较大)的待闸船舶，我们需要求得如何以最少闸次将所有船舶输送过坝，用所有待闸船舶的总吨位/最少需求次数，最终得到最大一次过闸平均吨位。即G=∑g/最少过闸次数。

于是船舶过闸问题就可以转化为一个二维切割模型，又在基础资料中已经论证船闸宽度为34 m，根据代表船型的宽度取值范围我们知道，闸室内一定能够停泊两列船舶，且船舶停靠方向与闸室长边水平。由此我们可以只计算半宽船闸内的船舶排列方式，将二维切割模型转化为一维切割模型。

参考上文中对约束条件的简化，易知原模型可以简化为线性规划模型。

对于船舶过闸问题，设计代表船型数量有限，故可以采用穷举的方式确定船舶过闸模式。

在闸室的某一特定长度(L)下，取代表船型中最短船舶长度(Wmin)，则此半宽船闸的最大船舶容纳数(K)由下式求得:K=L/Wmin

定义一种新的组合运算方法:F(m，n)。意义为在a1，a2，a3，L，amm种数量充分的物体中，取出n个物体的不同取法的数量。在船舶过闸问题中，由于绝大部分方案的过闸艘次小于最大船舶容纳数(K)，所以既有船闸类型数量确定的条件下，我们需要再加入一类船舶，此类船舶长度为0，是过闸船舶数量与最大船舶容纳数(K)相等。设入闸船舶类型数量为N，则半宽船闸过闸船舶全组合数量为F(N，K)。

易知:F(1，K)=1，F(N，1)=N，可以通过以下方法建立矩阵递归算出此半宽船闸过闸船舶组合方式的数量。F(N，K)=F(N，K-1)+F(N-1，K)

利用计算机穷举出所有半宽船闸过闸船舶组合方式后，再遍历每一种方式，舍弃不可用组合方式。剩下的组合方式F有效(N，K)即是线性规划模型中的约束条件。建立线性规划模型对原问题进行求解。

［1］张玮，廖鹏，粱应辰，宋德星．船闸通过能力计算中的若干问题研究［J］．武汉理工大学学报(交通科学与工程版)，2005

［2］王娜．背包问题的研究与算法设计［D］．昆明理工大学，2012

［3］田大肥．二维装箱问题的遗传算法求解［J］．舰船电子工程，2014