六相感应电动机调速系统的建模与仿真

屈鲁，谢卫，卢颖娟，张贻旭

(上海海事大学物流工程学院，上海 201306)

0 引言

电力电子技术的发展，使得三相感应电动机的变频调速技术得到广泛应用.但是，三相感应电动机系统可靠性不足，只要有一相出现故障，就会导致系统崩溃;并且在大功率场合下，由于功率开关器件的串并联会出现不均压和不均流等一系列问题.与三相感应电动机系统相比，多相感应电动机系统在许多方面，尤其是在大功率场合具有突出的优势.在电动机容量一定和相电流不变的情况下，随着电动机定子相数的增加，所需供电电压降低，可用低压功率器件实现大功率，避免由功率器件串并联带来的问题.此外，对于多相感应电动机系统，当其中一相或多相退出运行或缺相运行时，系统无须停机，仍然可以稳定运行，系统运行可靠性提高.目前，多相感应电动机及其调速系统在电动汽车、船舰推进、航空航天等领域的研究和实践日益增加.［1－2］

本文主要研究六相感应电动机调速系统的建模及仿真.六相感应电动机的转子绕组仍为常见的鼠笼结构，定子绕组采用两组互差30°电角度的对称三相绕组构成的六相双Y型结构.若将鼠笼形转子绕组也等效为类似的六相双Y型绕组，则六相感应电动机的物理模型可用图1表示.研究表明，采用这种绕组结构可以有效削弱转矩脉动，大幅度减小电机的损耗，提高电动机的极限容量.

1 六相感应电动机的数学模型

为便于分析，同时也满足工程实际所需的精度要求，可作如下假设:

(1)定子、转子表面光滑，无齿槽效应，气隙均匀;

图1 六相感应电动机的物理模型

(2)不计铁磁饱和、磁滞、涡流影响及导体趋肤效应;

(3)气隙磁场正弦分布，忽略磁场高次谐波的影响.

1.1 三相静止A－B－C坐标系的数学模型

根据上述假设条件，由六相感应电动机的物理模型及电磁关系，可得其在三相静止A－B－C坐标系下的数学模型［3－4］.

1.1.1 磁链方程

六相感应电动机在A－B－C坐标系下的磁链方程为

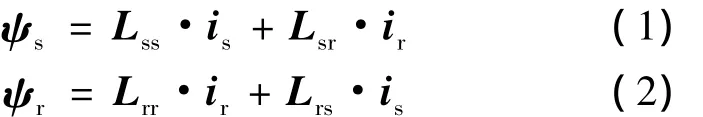
式中:ψs为定子磁链向量;ψr为转子磁链向量;is为定子电流向量;ir为转子电流向量;Lss为定子自感矩阵;Lrr为转子自感矩阵;Lsr=LrsT为定、转子互感矩阵.

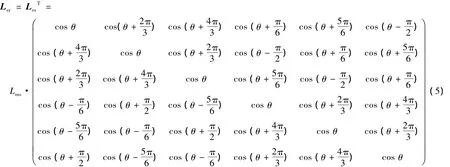
式中:Lls为定子等效两相绕组的自感;Llr为转子等效两相绕组的自感;Lms为定子与转子同轴等效绕组间的互感;θ为转子a1相与定子A1相之间的夹角.

1.1.2 电压方程

六相感应电动机在A－B－C坐标系下的电压方程为

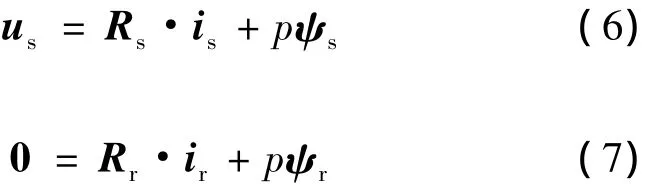
式中:us为定子电压向量;Rs为定子电阻矩阵;Rr为转子电阻矩阵.

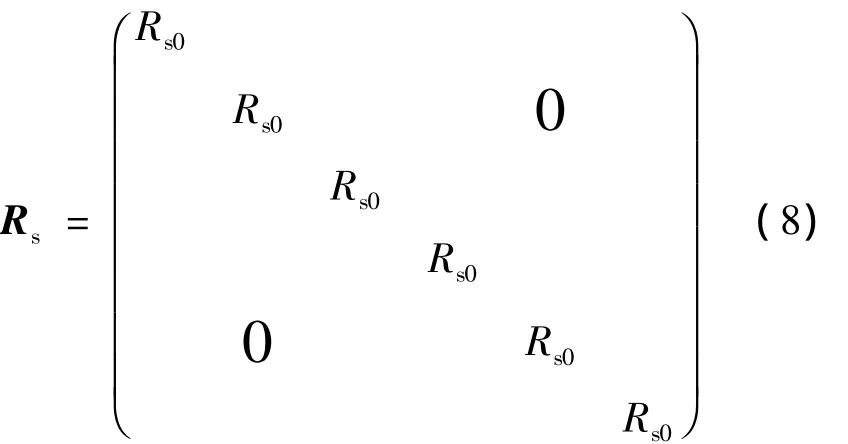
式中:Rs0是定子每相电阻;Rr0是转子每相电阻.

1.1.3 转矩方程与运动方程

六相感应电动机在A－B－C坐标系下的转矩方程为

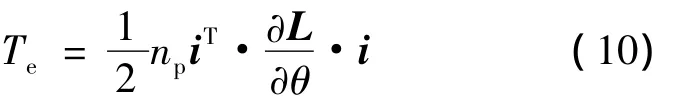
若忽略电力拖动系统传动机构中的黏滞性摩擦和扭转弹性，则六相感应电动机在A－B－C坐标系下的运动方程为

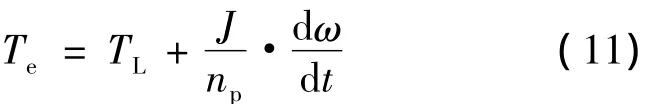
式中:TL为负载转矩;ω为转子角速度.

1.2 两相旋转d－q坐标系的数学模型

六相感应电动机在A－B－C坐标系下的数学模型是一个高阶、非线性、强耦合的多变量系统，可以通过坐标变换对其进行降阶、化简，由此建立六相感应电动机在d－q坐标系下的数学模型.满足功率不变和磁动势不变的变换矩阵及其逆矩阵［5］如下:

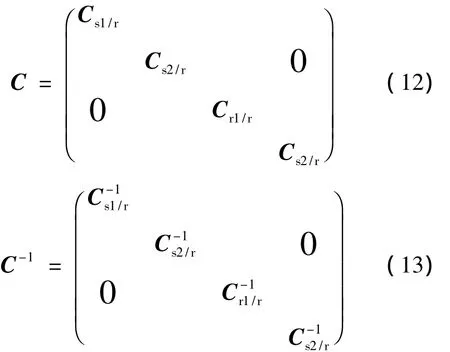
其中:

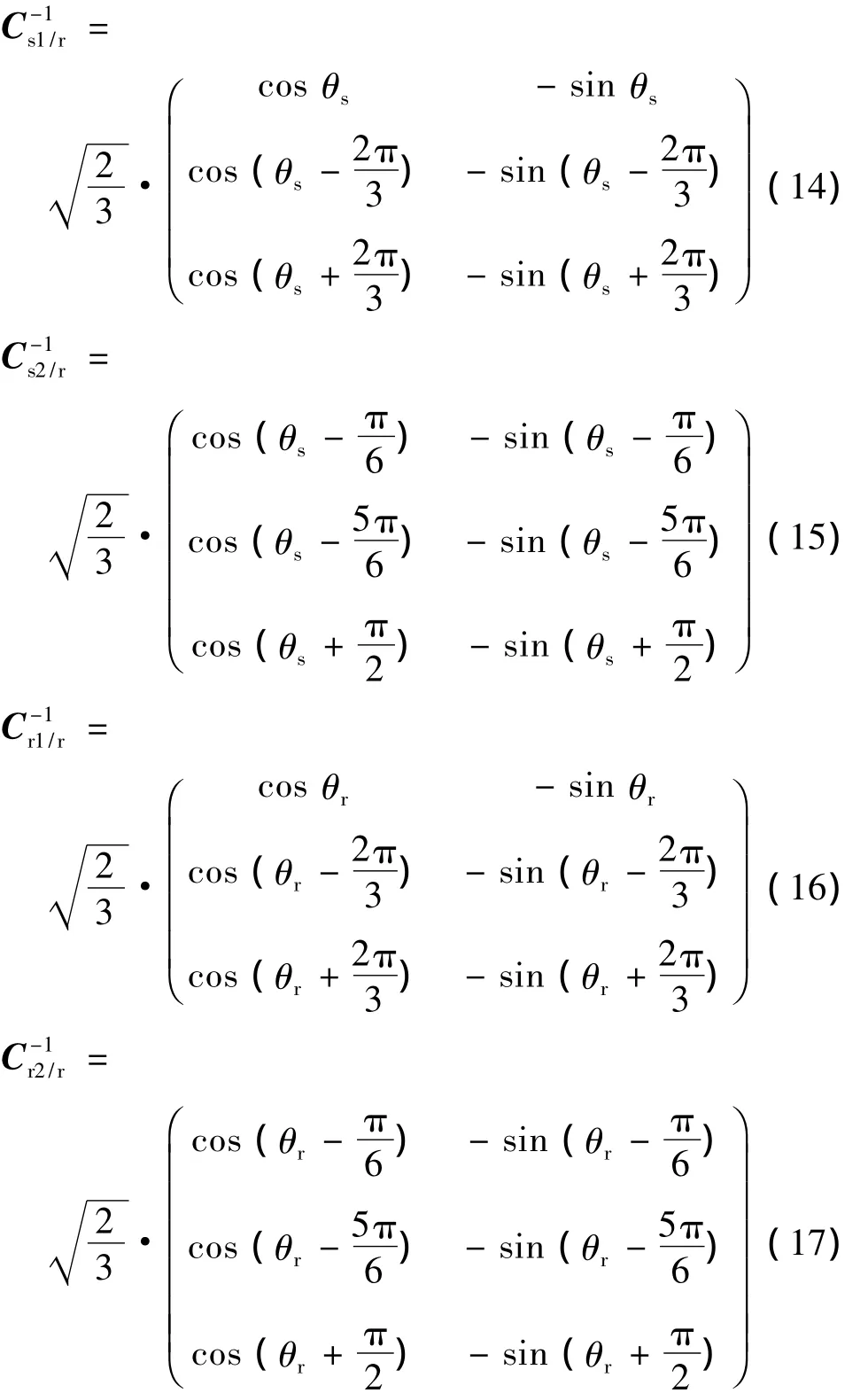
式中:θs为d轴与A1轴之间的夹角;θr为d轴与a1轴之间的夹角.

1.2.1 磁链方程

六相感应电动机在d－q坐标系下的磁链方程为

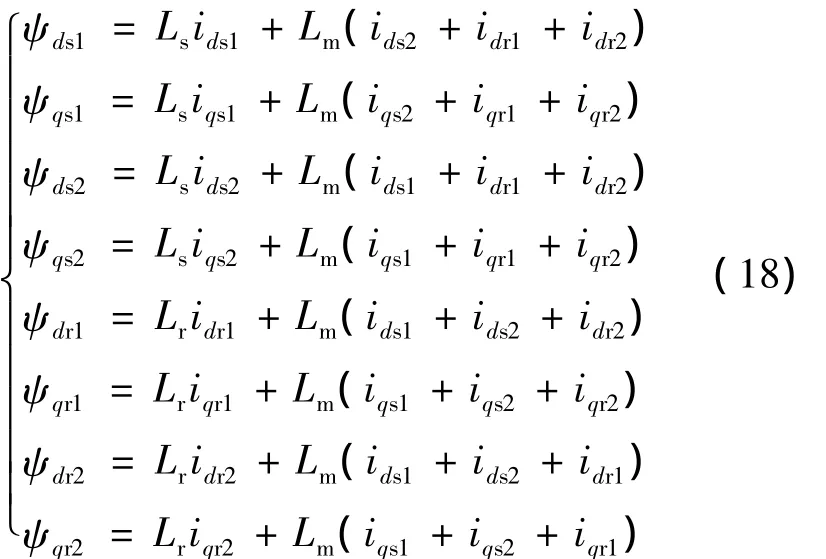
式中:Lm=1.5Lms，为d－q坐标系同轴定子与转子等效绕组间互感;Ls=1.5Lms+Lls，为 d－q坐标系定子等效两相绕组自感;Lr=1.5Lms+Llr，为 d－q坐标系转子等效两相绕组自感.

1.2.2 电压方程

六相感应电动机在d－q坐标系下的电压方程为

式中:ωdqs为d－q坐标系相对于定子A1相的角转速;ωdqr为d－q坐标系相对于转子a1相的角转速.

1.2.3 转矩方程与运动方程

六相感应电动机在d－q坐标系下的转矩方程为

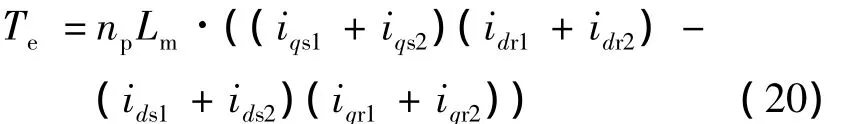
运动方程为

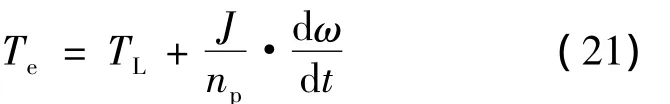
2 SVPWM技术

六相感应电动机采用电压源型逆变器供电时，定子电流谐波较大，这是因为定子绕组的阻抗较小.解决这一问题的有效方法是采用空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)技术.

六相感应电动机定子采用双Y型绕组，其中定子绕组A1，B1，C1可由图2所示的六相桥式电压源型逆变电路的(一)组逆变电路供电;定子绕组A2，B2，C2由逆变电路的(二)组供电.［6］

图2 六相桥式电压源型逆变电路

当进行SVPWM时，可采用两组相位差为30°电角度的三相对称正弦波作为调制信号和同一个三角载波信号进行调制，生成两组触发脉冲控制逆变器上器件的通断，由此产生两组相位差互为30°电角度的SVPWM波，其基本电压空间矢量分布见图3.

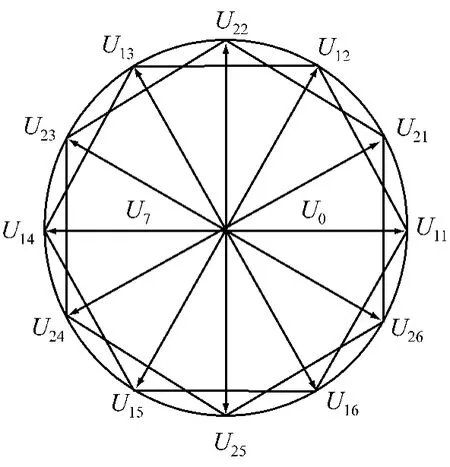
图3 六相逆变器SVPWM基本电压空间矢量分布

3 MATLAB建模及仿真

3.1 SVPWM电压源型逆变器的建模仿真

按照上述SVPWM原理，在SIMULINK环境下建立SVPWM六相电压源型逆变器的仿真模型并进行仿真，有关参数:直流电压1 000 V，正弦波频率50 Hz，三角波频率1 860 Hz.仿真所得的逆变器输出相电压波形见图4.

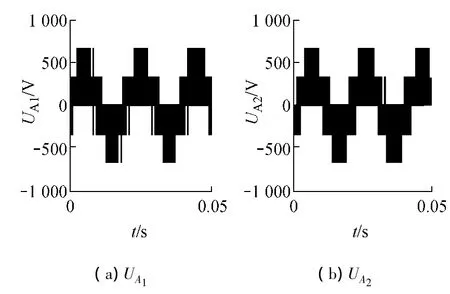
图4 逆变器输出电压UA1和UA2

3.2 六相感应电动机调速系统的建模仿真

根据六相感应电动机在d－q坐标系下的数学模型，在SIMULINK环境下建立基于两相同步旋转坐标系下的六相感应电动机仿真模型，主要包括电压、磁链和转矩等3个子模块，见图5.由SVPWM六相电压源型逆变器供电，进行电动机起动和回馈制动的仿真.

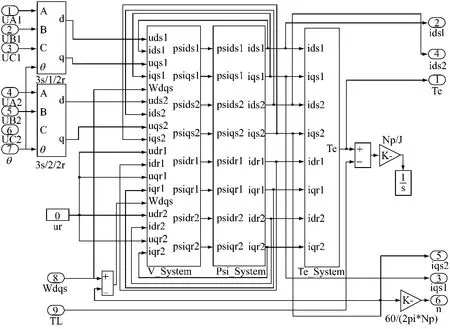
图5 六相感应电动机的仿真模型

六相感应电动机额定数据如下:np=3，f1=50 Hz，Rs=0.22 Ω，Rr=0.47 Ω，Ls=0.039 5 H，Lr=0.039 5 H，Lm=0.036 4 H，J=0.116 N·m2.3.2.1 起动仿真

令负载转矩为零，仿真结果见图6.

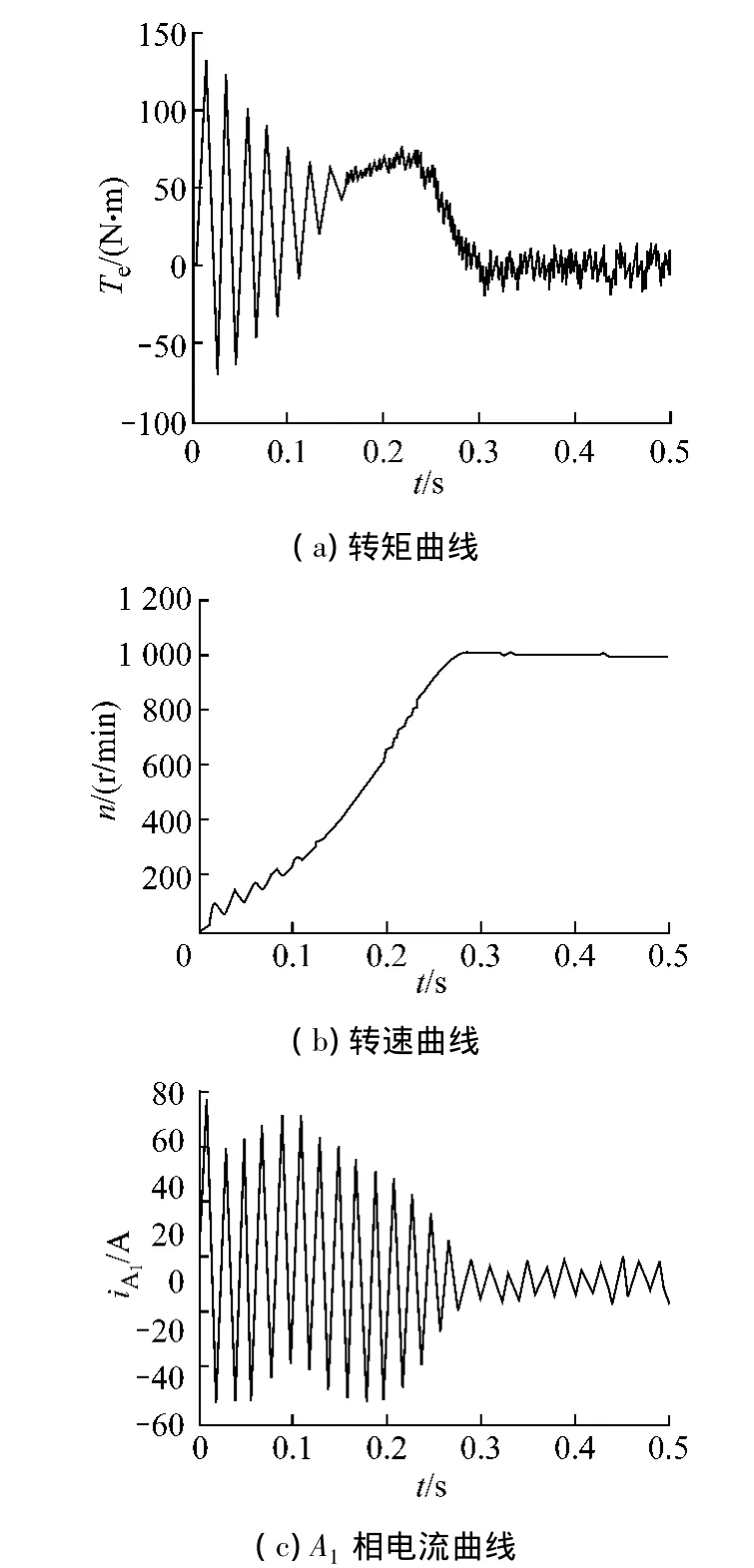
图6 起动仿真结果

由仿真结果可知，空载直接起动只需0.3 s，转速就稳定在同步转速上.

3.2.2 回馈制动仿真

当电动机空载运行0.5 s之后，将负载转矩改成负值，进入回馈制动过程，仿真结果见图7.

图7 回馈制动仿真结果

由仿真结果可知，当电机转速超过同步转速时，电机进入发电状态，向电网回馈电能，仅需0.1 s就达到稳定，动态性能好.

4 结束语

在MATLAB/SIMULINK环境下，建立SVPWM六相电压源型逆变器供电的六相感应电动机调速系统的数学模型和仿真模型，并在此基础上分别进行直接空载起动和回馈制动的动态仿真.通过仿真结果分析，可知六相感应电动机调速系统具有较好的的动态性能和稳态性能.

［1］SMIRANDA R，JACOBINA C B，LIMA A M N.Modeling and analysis of six－phase induction machine under fault condition［J］.IEEE Trans on Energy Applications，2009，4(9):824－829.

［2］金爱娟，李少龙，任永德，等.六相感应电机的SVPWM技术研究［J］.测控技术，2004，23(6):40－42.

［3］LIN Chen，FAN Yang.Unified voltage modulation method for dual three－phase induction machine［J］.IEEE Proc 3rd Int Conf Machine Learning ＆Cybernetics，2004，26(29):672－677.

［4］李山，王明渝，刘和平.基于DSP的六相感应电机矢量控制系统设计［J］.大电机技术，2005(3):23－26.

［5］陈伯时.电力拖动自动控制系统［M］.3版.北京:机械工业出版社，2003:63－270.

［6］ZHAO Y，LIPO T A.Space vector PWM control of dual three－phase induction machine using vector space decomposition［J］.IEEE Trans Industry Applications，1995，31(5):1100－1109.