c－幂零群与幂零群

冯海辉

(上海海事大学 文理学院，上海 201306)

0 引言

在有限群论的研究中，幂零群是一类重要的可解群.因此，刻画有限群的幂零性成为一个研究重点，许多学者［1－3］已经从各个不同的角度对其进行研究.特征标理论是研究有限群的一个重要工具，如文献［4］利用特征标理论给出一个群是幂零群的充分性条件:N－群是幂零群.为了研究特征标理论中的一个基本问题——一个拟本原特征标三元组在什么条件下也是一个本原特征标三元组，文献［5］借助χ－幂零群的概念给出完整的回答.有限群的χ－幂零性仅仅是某种局部的幂零性，它与群的幂零性之间有一种内在的联系，因此可以从特征标这个角度给出有限群幂零性的完整刻画.本文引入c－幂零群的概念，并且利用这个概念给出一个有限群为幂零群的充要条件.

文中的群均为有限群，所使用的符号和术语都是标准的，可参考文献［6－7］.

1 引理

1.1 χ-幂零群的定义

定义1设G为一个群，ψ为G的一个复特征标.称G为ψ－幂零群，是指对G的每个极大子群M及M的每个复特征标 φ，如果满足 φG=ψ，则有M◁G.［2］

由于幂零群的每个极大子群均正规，当G为幂零群时，对每个χ∈Irr(G)，G均为χ－幂零群.

1.2 c－幂零群的定义

定义2设G为一个群，若对每个不可约特征标 χ∈Irr(G)，G 均为 χ－幂零群，则称 G 为 c－幂零群或特征标幂零群.

显然，由前面的讨论知道幂零群一定是c－幂零群，但是反过来不一定正确，即c－幂零群不一定是幂零群.

例如:取 G=S3，Irr(G)={λ1，λ2，χ}，其中 λ1，λ2为线性特征标，χ为2次不可约特征标.显然G是λi－幂零的，i=1，2.下面说明 G 也是 χ－幂零群.因为χ为M－特征标，从而χ可以由G的某个子群的线性特征标λ诱导，设为χ=λG，其中λ∈Irr(H)，H≤G.由次数公式可得2=χ(1)=|G:H|，从而H◁G.于是G为c－幂零群，但G不是幂零群.

1.3 两个引理

引理1设N为群G的一个正规子群.［1］

(1)若χ为G的一个复特征标，且N≤Ker(χ)，则χ在G关于N的陪集上取常值，且如下定义的函数为 G/N 的特征标:(Ng)=χ(g)，∀g∈G.

(3)由(1)和(2)可知，χ∈Irr(G)当且仅当 χ^∈Irr(G/N).

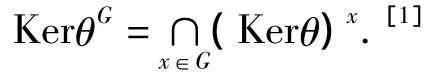
2 主要结果

首先给出c－幂零群的几个性质.

定理1设G为c－幂零群，且N为G的正规子群，则商群G/N亦为c－幂零群.

证明令=G/N.任取复不可约特征标∈Irr()，且为的一个极大子群∈Irr()满足=，其中=H/N.由引理 1 有 θG= χ，且 H 为 G的极大子群.由G为c－幂零群得H=HG◁G.从而H/N◁G/N，即◁，故为 χ－幂零群.由 χ^的任意性知为c－幂零群.证毕.

对于幂零群，若商群G/N为幂零群，则不一定有G为幂零群.对于χ－幂零群，有下面的结论:

定理2设N为群G的一个正规子群为商群G/N的一个复特征标，若G/N为－幂零群，则G为χ－幂零群，其中χ由提升得到.

证明记=G/N.设H为G的一个极大子群，θ∈Irr(H)，且 θG= χ.由引理 2 知 Kerχ≤Kerθ，故有N≤Kerχ≤Kerθ≤H.由引理1 有≤，且=其中由为幂零群知也即为的真子群，故有HG＜G为真子群.再由H的极大性知H◁G，从而由定义1知G为χ－幂零群.证毕.

设 χ1，χ2，…，χn为群 G 的全部不可约特征标，令Γ ={Kerχi|i=1，2，…，n}为 G 的不可约特征标核构成的集合.记Δ为Γ中元素在集合的包含关系下的极小元构成的集合.下面的定理给出c－幂零群的一个刻画.

定理3群G为c－幂零群当且仅当对每个不可约特征标 χ∈Irr(G)，只要 Kerχ∈Δ，就有 G/Kerχ为c－幂零群.

证明由定理1知必要性是显然的.

充分性.任取不可约特征标ψ∈Irr(G)，则存在G的一个不可约特征标 χ，使得 Kerχ∈Δ 并且Kerχ≤Kerψ.在定理2 中令 N=Kerχ，则 G 为 ψ－幂零群，从而G为c－幂零群.证毕.

下述定理给出幂零群的一个刻画条件，是本文的主要结论.

定理4群G为幂零群当且仅当对G的每个复特征标ψ，均有G为ψ－幂零群.

证明必要性.设G为幂零群，由定义2可知对G的每个复特征标ψ均有G为ψ－幂零群.

充分性.对G的每个极大子群M及M的每个复特征标φ，根据特征标的诱导定理，φG必为G的复特征标，从而由条件可知G为φG－幂零群.再根据定义2可知M◁G，因此G为幂零群.证毕.

由此可知，如果对任意不可约特征标χ∈Irr(G)均有G为χ－幂零群，还不能完全刻画群的幂零性，即c－幂零群未必是幂零群.下述定理给出一个c－幂零群在什么条件下是幂零群的充分性条件.

定理5设G为c－幂零群，Φ(G)为G的Frattini子群.若存在χ∈Irr(G)，使得χ可以从Φ(G)的某个子群的特征标来诱导，则G为幂零群.

证明设 χ=θG，其中 θ∈Irr(H)，H≤Φ(G).由Frattini子群的定义可知，对G的每个极大子群M均有H≤M.再由G为χ－幂零群可知M◁G，从而G为幂零群.证毕.

［1］CAMINA A R，CAMINA R D.Recognising nilpotent groups［J］.J Algebra，2006，300(1):16－24.

［2］COSSEY J，HAWKES T，MANN A.A criterion for a group to be nilpotent［J］.Bull London Math Soc，1992，24(3):267－270.

［3］ITÔN.On finite groups with given conjugate type I［J］.Nagoya Math J，1953(6):17－28.

［4］BERKOVICH Y，ZHMUD E.Character of finite groups:part 2［M］.New York:American Mathematics Soc，1999.

［5］冯海辉，靳平.特征标三元组的诱导子和限制子［J］.山西大学学报:自然科学版，2006，29(S):6－7.

［6］ISAACS I M.Character theory of finite groups［M］.New York:Academic Pr，1976.

［7］KURZWEIL H，STELLMACHER B.The theory of finite groups［M］.New York:Springer，2003.