粤北刘家山地区多元素分形维数谱函数及其对矿化的指示分析*

张 焱,周永章,黄 锐,李文胜,吕文超,王林峰,郑 蕾，何 翔

(1.中山大学地球科学系∥广东省地质过程与矿产资源探查重点实验室,广东 广州 510275；2.广东省地质调查院,广东 广州 510200；3.武汉地质工程勘察院,湖北 武汉 430051)

通常多重分形可描述为多个单一分形在空间的相互缠结、镶嵌,它是单一分形的推广[1-5]。有关多重分形理论前人已做过较多研究,如它可用来解释许多统计分布和空间统计分布中的疑难问题[6],可用于描述地质地球化学领域许多测度的分布规律[7-14],用于分离地球化学场中的背景与异常来描述矿化区域[15-19],也有了许多参数来表示和判断分形与多重分形方法。 综合了分离背景和异常的浓度-面积法(C-A)和分形滤波(S-A)技术并用于矿产资源定量预测的GIS软件系统(GeoDAS GIS)也已成型[20]。由于在实际的应用工作中,大多学者专注于个别成矿元素的研究,且研究区一般只集中于部分元素或矿区相对集中的区域,工作主要是偏于理论研究,与实际应用还有差距。

故本文采用统计方法与多重分形方法对比分析来研究粤北刘家山地区地球化学元素的分布规律。

1 研究区概况

刘家山铅锌矿区位于广东省始兴县城162°方向[21],平距约24 km处,面积约10 km2。 该区总体属中低山地区,水系非常发育,地形切割强烈，常形成悬崖峭壁等险峻地形，该区矿产主要有锌、铅、铜、银、钨等。北面有石人嶂、梅子窝、师姑山等中小型钨矿床; 南西面有新凉亭、寨背坑等小型铜铅锌多金属矿床(图1)。

本文收集了刘家山区域内1 573个水系沉积物样品中与成矿密切相关的12种元素含量数据,在此用于研究元素分布规律。

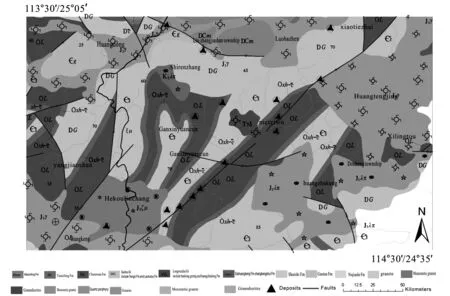
图1 研究区地质矿产略图

2 多重分形与谱分析法

多重分形所描述的是定义在某一面积或体积中的一种度量,若这种度量具有空间自相似性或统计自相似性,则可被称为多重分形。其度量值或数值的奇异性可将定义的区域分解成一系列空间上相互镶嵌的子区域,各个子区域构成单个分形.这样形成的分形同时具有分形维数和各自度量的奇异性。一系列的分形维数和奇异性构成维数谱函数。有关多重分形谱函数建立的详细过程前人已做了较多研究[1,14,22-25],计算维数谱函数的方法有多种[1,7,14],其中矩方法为最常用的方法之一,利用矩方法可计算出奇异性指数α和分形维数f(α),通过对地球化学元素的奇异性指数和分形维数进行分析研究可得知元素的空间分布模式。前人使用奇异性指数α的最大值和最小值来描述分形强度[26],使用参数R=(ΔαL-ΔαR)/(ΔαL+ΔαR)描述元素之间高低浓度的相关性[23]。

3 元素分布规律

3.1 统计法

文中采用Q-Q图来分析地球化学元素的统计频率分布特征,Q-Q图可以直观检验元素是否服从正态或对数正态分布。对该研究区几种主要元素含量进行分析结果见图2。从图2中可看出Pb、Zn元素低含量部分基本服从正态分布或对数正态分布,而高含量区却偏离正态分布或对数正态分布。实际上这些高含量值服从分形分布,研究表明,地球化学元素的背景值和异常值会满足不同的分布。分析刘家山地区其它的10种元素也得到相似的结果。

然后对该区地球化学数据进行统计聚类分析,其目的是将相似程度较大的数据划为一类,这样每个子集具有共同的特征,这一过程可通过聚类分析图实现[27]。聚类分析的结果将这12种元素分为2大类(图3):① Pb-Zn-Cu-Bi-W-Ag-As-Sb;② Mo-Hg-Sn-Be,并计算Pb、Zn、Cu三种元素与其他各元素的相关系数(表1)。从分类结果可看出该区域主要成矿元素Pb、Zn与Ag、Sb相关系数较高，可能与铅锌矿化有关；Cu与W、Bi、Ag、As相关系数较高，是寻找斑岩型铜矿床的指示。

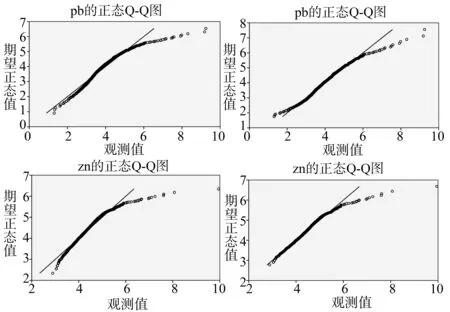
图2 刘家山地区Pb、Zn元素含量统计分析结果

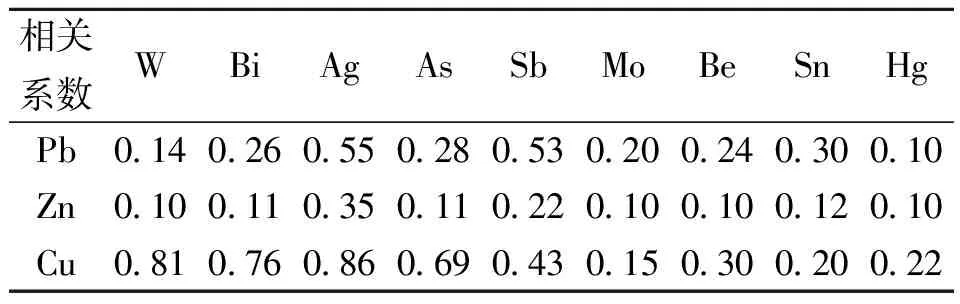
表1 相关系数矩阵

同时对其他几种元素含量分布进行研究发现Be、Sn异常分布走向最为接近,分散的异常区域沿NW对角线和正南方向分布。其它8种元素Cu、Ag、W、Sb、As、Bi、Hg、Mo异常走向与成矿主元素Pb、Zn大体一致。

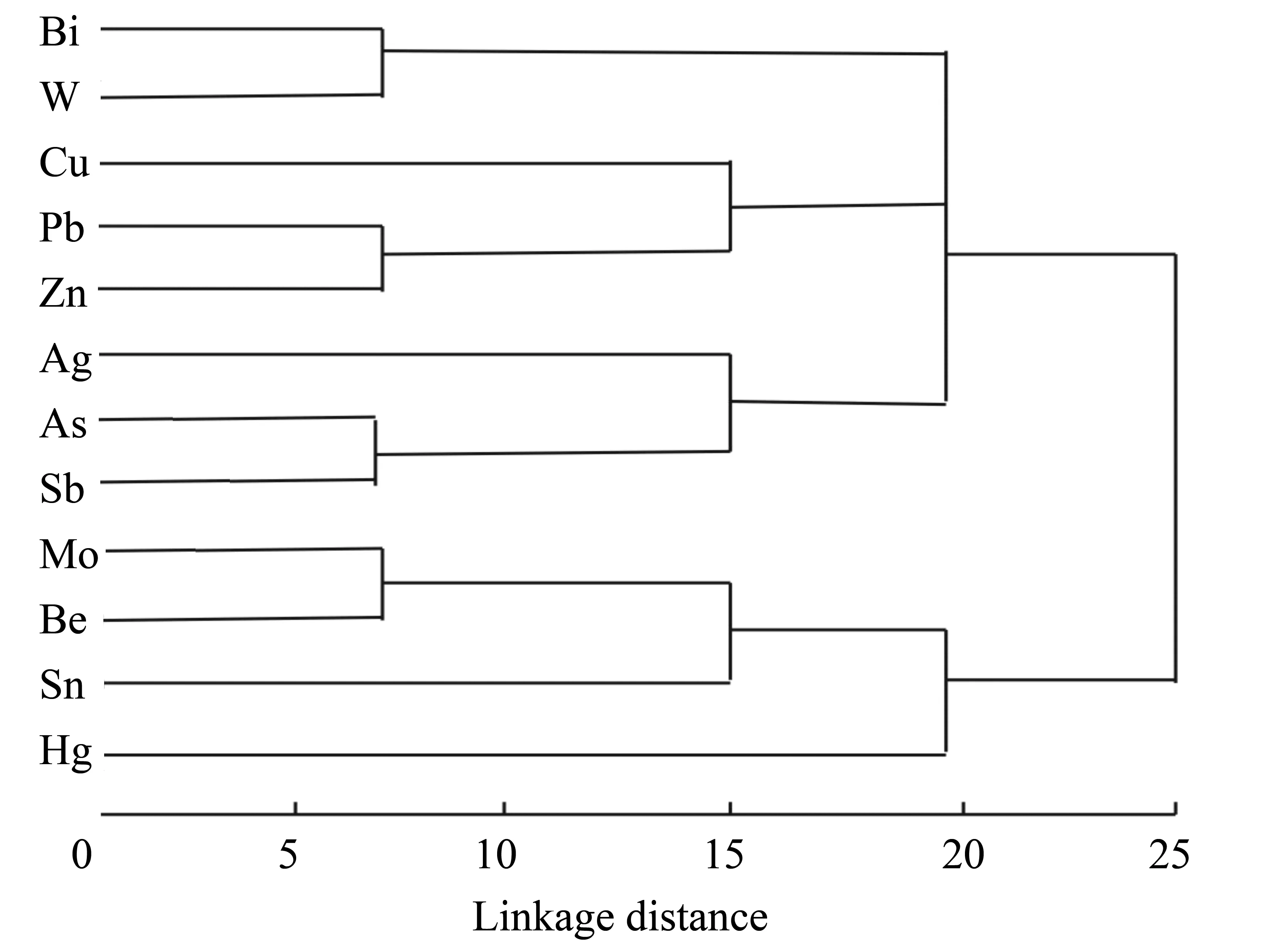
图3 聚类分析图

3.2 多重分形法

分形模型为:

N(R>r)=Kr-Dr>0

(1)

R表示特征尺度(统计元素给定的限定条件),如大于某个含量元素的含量值、距离、金属矿的品位等;K>0,为比例常数；D>0,为分维数；N(r)=N(R≥r),表示特征尺度大于等于r的数目(大于等于某个限定条件的元素统计值，如面积)。

C-A分形法由Cheng等首先提出[28],是用来分选地球化学异常的。从多重分形观点来看,一些极端值(地球化学中的异常值)可能遵循分形分布而不是正态或对数正态分布。 C-A法是基于浓度值的从背景中分离异常值的方法,这些量值也可以是地球化学指标的空间和几何特征。由于不同地质过程产生的元素分布其含量值和分布频率都会有所不同,而且其形态也有线状、环状或面状的差异,这是符合地质实际的[13]。有关C-A方法的具体过程参见[28]。

采用C-A分形方法所计算的面积与含量的关系可见图4。横坐标表示等值线的值,纵坐标表示等值线所包围的面积。随着等值线值的增大,其内部所包围的面积相应减小(随着等值线值增大,它所包围的面积趋于定值,故在高含量部分呈现重复的点)。各元素C-A分形图与Q-Q图对比可以看出Q-Q统计图由于不考虑异常的空间形态和变化性,该区内背景和异常值在Q-Q图上没有明确分界,而C-A分形法由于考虑了元素含量随异常空间变化而改变,故背景和异常值在C-A图上呈现出截然不同的模式。这些值可分别用两种Power-law函数所表达(采用最小二乘法拟合直线段)。从分析结果图得知2种模型分界点所对应的等值线值分别为92.55×10-6、196.53×10-6、36.66×10-6,经与其他资料比较研究得知,这些分界值可作为本区的局部Pb、Zn、Cu矿化异常的下限。同时出现的异常往往是矿异常,由锡铅银矿化引起[29]。这些标志对筛选找矿靶区有重要意义。

文中采用矩方法,步长为0.5取q值从-10到10计算12个元素的多重分形谱函数f(α)(图5)(横坐标为奇异性指数α,纵坐标为分形维数谱函数f(α))

从图5可知，曲线左半边(对应异常值)主要反映q≥0的特征,重点显示了较高含量的特征[14]; 曲线右半边(对应相对较低值)q<0反映了分形结构中的细小结构变化,从而使得低含量的特征能得到加强。研究表明:该区域内的地球化学元素多重分形谱函数f(α)均成连续分布,f(α)均为不对称的上凸曲线,Sn、Be除外,表明该区域的地球化学场曾经历过不同程度的局部叠加。从谱函数图可明显看出Sn和Be左右曲线趋于对称状态,形态基本一致; 而其他的元素曲线均趋于左偏状态。为进一步分析Sn和Be元素分布规律对其进行C-A分解后比较发现(图5),Sn元素高异常区较Be集中,这可能与其他的控矿因素有关,后期地质工作者在此区发现了锡多金属矿(化)带,这也说明多重分形方法对指导地球化学异常工作的有益性。

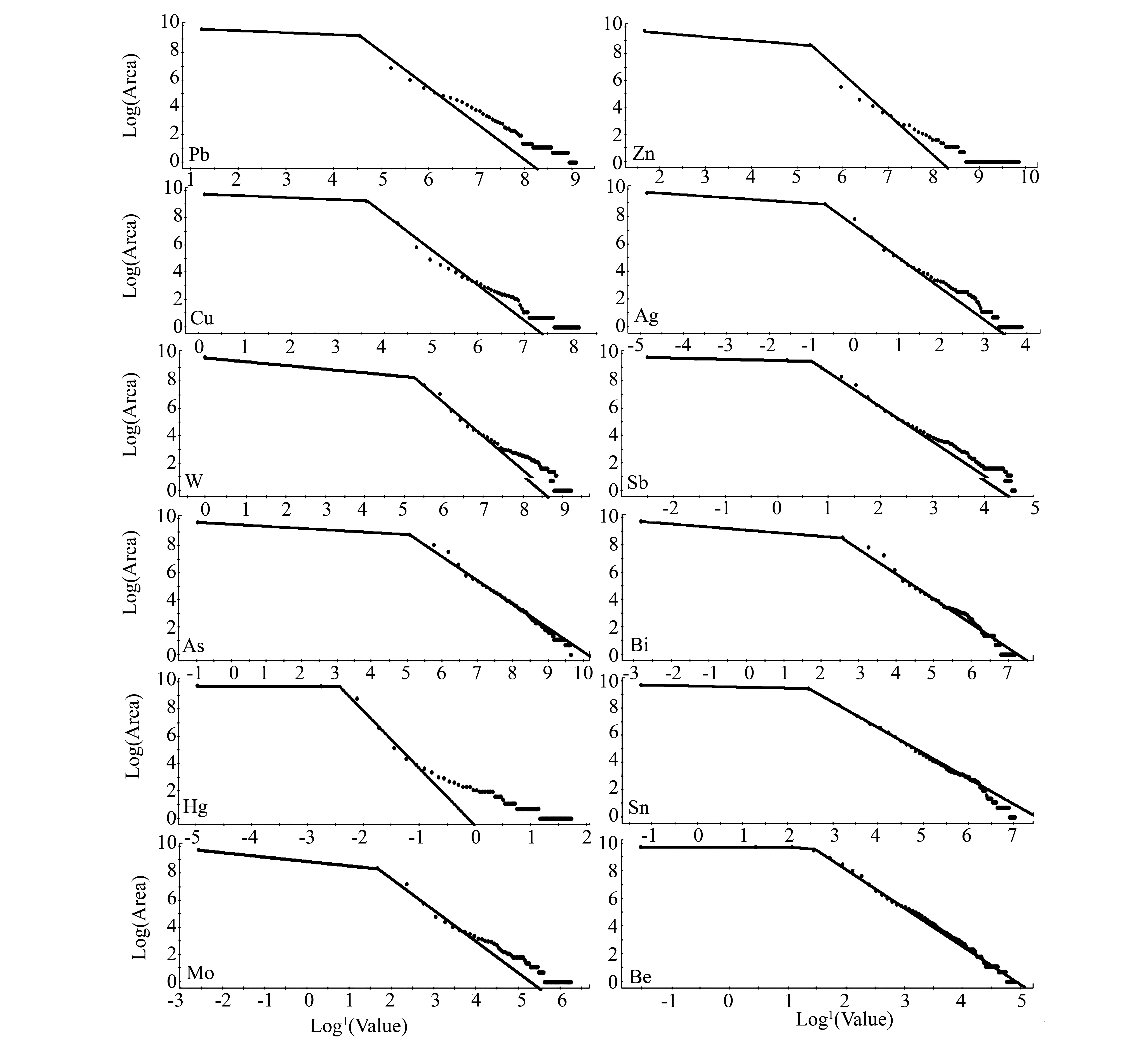
图4 各元素C-A分形分布

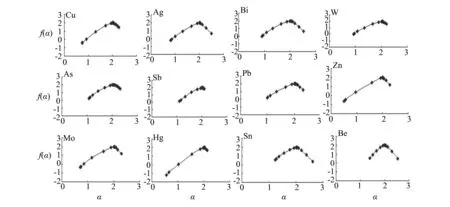
图5 粤北刘家山地区地球化学元素的多重分形谱函数

前人[17,30]采用参数法分析分形谱函数曲线,其中α0为q=0时α的值,

ΔαL=|α(min)-α0|

(2)

ΔαR=|α(max)-α0|

(3)

R=(αL-ΔαR)/(αL+ΔαR)

(4)

R=0时表示谱函数曲线两侧完全对称,R>0表示谱函数曲线向左偏,R<0表示谱函数曲线向右偏。表2列出了各元素谱函数的ΔαL、ΔαR和R值。

表2 刘家山地区地球化学元素参数一览表

图6 C-A分解后显示图

该区12种元素其R值均大于0,R值大小与元素的成矿潜力有一定的相关性,R值越大对应的f(α)曲线左半段相对右半段较宽(如Pb)，越容易成矿,结合本区实际情况由R值得知Pb、Cu、W、Sb、Hg、As这几种元素在该区极有利成矿,也即元素的多重分形谱函数的形态特征对元素的成矿潜力具有一定的指示意义。

4 结 论

由分形谱函数图观察可知,曲线图左半边较右半边弯曲越大,越有利于富集成矿,因为高含量部分比低含量部分平均变化差异大,故刘家山地区元素Pb、Zn、Cu、Ag、Bi、W、As、Sb、Mo、Hg对成矿有利,这也进一步说明了元素的多重分形谱函数的形态特征能为元素的成矿潜力评价提供重要的线索。

后期广东省地质调查院于张家山-刘家山一带开展1∶10 000土壤剖面测量(网度400×20m)及1∶10 000地质填图工作时发现了面积大、强度高、套合好、异常组份复杂的AP4异常,同时于AP4异常浓集中心发现了铅锌富矿体,结果表明，采用C-A分形法可以更有效地研究地球化学元素异常值的分布和富集规律。C-A分形法将统计方法中元素含量和频率分布和异常空间形态等有机的结合，对区分地球化学背景和与矿化有关的异常效果更好，为该地区元素的成矿潜力评价提供了重要的线索。由此得到该区具有良好的找矿远景的结论。

参考文献：

[1]EVERTSZ C J G,MANDELBROT B B.Multifractal measures(Appendix B)[C]∥Peitgen H O et al,eds.Chaos and Fractals.New York: Springer Verlag,1992:922-953.

[2]FEDER J.Fractals [M].New York: Plenum,1988.

[3]LOVEJOY S,SCHERTZER D.Multifractals,universality classes,and satellite and radar measurements of cloud and rain fields [J].J Geophys Res,1990,95(D3):2021-2034.

[4]STANLEY H E,MEAKIN P.Multifractal phenomena in physics and chemistry [J].Nature,1998,335(6189):405-409.

[5]张 焱,成秋明,周永章,等.分形插值在地球化学数据中的应用[J].中山大学学报:自然科学版,2011,50(1): 133-137.

[6]CHENG Q.Discrete multifractals[J].Math Geol,1997,29(2):245-266.

[7]CHENG Q,AGTERBERG F P.Multifractal modeling and spatial point processes[J].Math Geol,1995,27:831-845.

[8]CHENG Q.Mutlifractal modeling and lacunarity analysis [J].Math Geol,1997,29:919-932.

[9]SIM B L,AGTERBERG F P,BEAUDRY C.Determining the cutoff between background and relative base metal smeller contamination levels using multifractal[J].Comput Geosci,1999,25(9):1023-1041.

[10]CHENG Q.Markov processes and discrete multifractals[J].Math Geol,1999,31(4):455-469.

[11]CHENG Q.Gliding box method and multifractal modeling [J].Computer & Geosciences,1999,25(9):1073-1079.

[12]CHENG Q.Spatial and scaling modeling for geochemical anomaly separation[J].J Geochem Explor,1999,65:175-194.

[13]成秋明.多重分形理论与地球化学元素分布规律[J].地球科学,2000,25(3):311-318.

[14]AGTERBERG F P.Multifractal simulation of geochemical map patterns[C]∥Proceedings of the International Symposium on Diversity of Mineralization and its Prediction and Assessment.Beijing and Wuhan,2001:6-14.

[15]MATSCHULLAT J,OTTENSTEIN R,REIMANN C.Geochemical Background: Can We Calculate It? [J].Environmental Geology,2000,39(9):990-1000.

[16]CHENG Q.Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu,Yunnan province,China[J].Ore Geology Reviews,2007,32:314-324.

[17]GALUSZKA A.A review of geochemical background concepts and an example using data from Poland[J].Environmental Geology,2007,52(5):861-870.

[18]XIE S,CHENG Q,XING X,et al.Geochemical multifractal distribution patterns in sediments from ordered streams[J].Geoderma,2010,160(01):36-46.

[19]张焱,周永章,王正海,等.广东庞西垌地区地球化学组合异常识别与提取[J].地球学报,2011,32(5):533-540.

[20]CHENG Q.GeoData Analysis System(GeoDAS)for Mineral Exploration: User’s Guide and Exercise Manual,Material for the Training Workshop on GeoDAS[R].Canada:York University,2000.

[21]刘晋华,陈思祥,官卫忠.广东省始兴县刘家山矿区铅锌矿普查报告[R].广东省地质调查院,2004.

[22]HALSEY T C,JENSEN M H,KADANOFF L P,et al.Fractal measures and their singularities-the characterization of strange sets[J].Physical Review A,1986,33(2):1141-1151.

[23]XIE S,BAO Z.Fractal and multifractal properties of geochemical fields[J].Mathematical Geology,2004,36(7):847-864.

[24]ALI K,CHENG Q,CHEN Z.Multifractal power spectrum and singularity analysis for modeling stream sediment geochemical distribution patterns to identify anomalies related to gold mineralization in Yunnan Province,South China[J].Geochemistry: Exploration,Environment,Analysis,2007,7(4),293-301.

[25]XIE S.Identification of geochemical anomaly by multifractal analysis[J].Journal of China University of Geosciences,2008,19(4):334-342.

[26]KRAVCHENKO N A,BOAST W C,BULLOCK G D.Multifractal analysis of soil spatial variability[J].Agronomy Journal,1999,91:1033-1041.

[27]MACQUEEN J B.Some methods for classification and analysis of multivariate observation[C]∥Proceedings of 5-th Berkeley Symposium on Mathematical Statistics and Probability.Berkeley: University of California Press,1967:281-297.

[28]CHENG Q,AGTERBERG F P,BALLANTYNE S B.The separation of geochemical anomalies from background by fractal methods[J].Geochem Explor,1994,51: 109-130.

[29]张福来,朱祖良,刘晋华.粤北始兴鱼岔坑锡矿地球化学特征与找矿标志[J].华南地质与矿产,2005(4):11-17.

[30]XIE S,CHENG Q,CHEN G,et al.Application of local singularity in prospecting potential oil/gas targets[J].Nonlinear Processes Geophysics,2007,14:285-292.