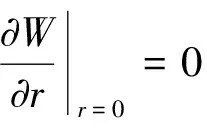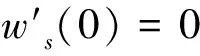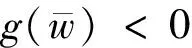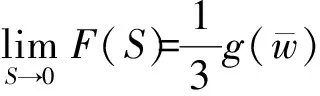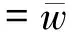一个肿瘤化学治疗空间结构模型的定性分析*
高帅帅,卫雪梅,冯兆永
(1.广东工业大学应用数学学院, 广东 广州 510006;2.中山大学数学与计算科学学院, 广东 广州 510275)
早在20世纪70年代人们就发现,肿瘤生长的基本规律在数学上可表述为偏微分方程的自由边界问题[1-2]。在生物和医学中,很多关于体内和体外肿瘤细胞生长的模型已被提出。随着人们研究的深入,考虑的参量越来越多,描述的肿瘤生长的自由边界问题的形式也越来越复杂。目前,关于这些自由边界问题的严格数学分析正在逐步深入地进行着,并且已经得到很多有意义的结果[3-9]。
本文研究了一个肿瘤化学治疗反应的空间结构模型。这个模型是Norris等在文[10]中提出来的。这里假设肿瘤生长模型是连续的(i.e.繁殖和死亡的过程是连续的),肿瘤细胞球体对称且是不可压缩的,药物按比例浓度抑制细胞生长。这是一个简单的肿瘤细胞生长模型,它使药物的化学治疗的效果尽可能的明显。这实质上是一个偏微分方程的自由边界问题。这个问题的具体模型如下:
,0
(1)
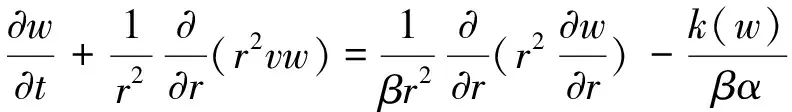
0
(2)
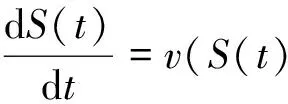
(3)
S(0)=1,w(r,0)=w0(r),0≤r≤S(t)
(4)
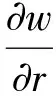
(5)
w(S(t),t)=w(t),t>0
(6)
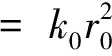
其中μ是药物效用函数,kd是一个临界药物浓度。易知Case(Ⅰ)线性动力系统和Case(Ⅱ)米氏动力系统有不同的形式,显然k(w)是Lipschitz连续的。
本文的主要目的是对这个非线性问题做严格的数学分析。我们将讨论以下3个问题:①局部解的存在唯一性;②整体解的存在唯一性;③稳态解的分布。
在第1-3节中,将在下面的假设下讨论整体解的存在唯一性:
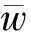
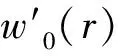
在第4节中将在下面假设下讨论稳态解的分布:
(B1)f∈C1[0,∞),f′(w)>0,f(0)=0(即对∀w>0,有f(w)>0),其中f(w)如第4节中定义)。
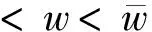
(B3)=(A2)。
本文主要结果如下:
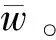
定理2 假设条件(B1),(B2)和(B3)满足,则下列结论成立:
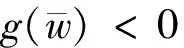
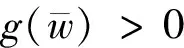
1 问题的简化
将(1)代入(2)可得一个等价的问题如下
,0
(7)
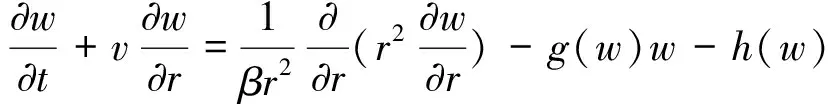
0
(8)
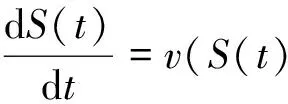
(9)
S(0)=1,w(r,0)=w0(r),0≤r≤S(t)
(10)
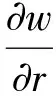
(11)
w(S(t),t)=w(t),t>0
(12)
其中
g(w)=kn-k(w),h(w)=k(w)/(βα)
显然g(w)和h(w)是Lipschitz连续的。
作变量替换
,τ
(13)
并记
u(z,τ)=S(t)v(r,t),η(τ)=S(t),n(z,τ)=w(z,t)
则自由边界问题(7)-(12)转换为在固定区域{(z,τ)|0≤z≤1,τ≥0}上的初边值问题如下:
η2(τ)g(n),0
(14)
u(0,τ)=0,τ>0
(15)
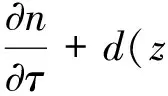
p(η,n)n-q(η,n),0
(16)
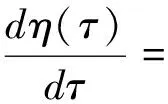
(17)
η(0)=1,n(z,0)=n0(z),0 (18) (19) n(1,τ)=n(τ),τ>0 (20) 其中 d(z,τ)=u(z,τ)-zu(1,τ) 且 p(η,n)=η2(τ)g(n),q(η,n)=η2(τ)h(n) (21) 上面的结果可以总结为如下引理。 引理1 在变量替换(13)下,初边值问题(14)-(20)与自由边界问题(7)-(12)是等价的。 下面我们将介绍一个基本引理,首先引进一些记号: (i)记QT={(z,τ)|0 ∈Lp(QT),m+2k≤2} u(·,0)=φ)} 0 w(z,0)=w0(z),0≤z≤1 ≤Cp(T)(‖w(τ)‖W2,p(0,T)+ ‖w0(z)‖Dp(0,1)+‖f‖p) 且有如下估计: ‖w‖∞≤max{‖w(t)‖∞,‖w0‖∞}+Ted0T‖f‖∞ 其中 证明参见文献[3]。 这部分将证明系统(14)-(20)有唯一的整体解。先通过运用压缩映像原理证明系统(14)-(20)有唯一的局部解。由g(w),h(w)是Lipschitz连续的和(21)知p和q是Lipschitz连续的。记 对给定的T>0,引进度量空间(XT,d)如下:XT由向量函数(η,n)=(η(τ),n(z,τ))(0≤z≤1,0≤τ≤T)组成,满足如下条件: 定义XT中的度量d为 d((η1,n1),(η2,n2))=‖η1-η2‖∞+‖n1-n2‖∞, 0≤z≤1,0≤τ≤T 显然(XT,d)是一个完备度量空间。由式(14)-(15)可得 (22) (τ)u(1,τ),τ>0 (23) (24) (25) (26) (27) 首先证明F是XT到XT上的映射。 τ,0≤τ≤T (28) (29) 结合式(28)得 ‖∞≤C(T) (30) 其次要证当T充分小时,映射F是压缩的。设(ηi,ni)∈XT,i=1,2,则 (31) di(z,τ)=ui(z,τ)-zui(1,τ), d=d((η1,n1),(η2,n2)) 由式(31),g(n)的Lipschitz连续性,|g(n)|≤A和|η(τ)|<2,计算可得 |u1(z,τ)-u2(z,τ)|≤C(T)d (32) 利用(28),有 ≤TC(T)d (33) (34) (35) (36) 其中 ‖F‖∞≤C(T)d (37) 对问题(34)-(36)应用引理2,再结合式(37)可得 ≤T‖F‖∞≤TC(T)d (38) 结合式(33)、式(38),可以推出 d((η1,n1),(η2,n2))≤TC(T)d 因此,当T足够小时满足TC(T)d<1,此时F为压缩映射。 应用Banach不动点定理,可知当T足够小时F在XT中有唯一的不动点(η(τ),n(z,τ)),它是系统(14)-(20)的局部唯一解,其中0≤τ≤T。 定理3 条件(A1)和(A2)满足,当0 定理4 系统(14)-(20)的解对所有的t≥0都存在。 证明由式(17)和式(29)得 ≤≤,0≤τ (39) ≤η(τ)≤,0≤τ (40) 由引理2知 ≤C(p,T) (41) 由系统(14)-(20)与系统(1)-(6)的等价性得知,系统(1)-(6)的整体解存在且唯一。因此,定理1得证。 考虑如下边值问题: ΔrW=λf(W),0 (42) (43) 其中λ是一个非负参数。 引理3 假设条件(B1)满足,则对任意的λ>0,问题(42)-(43)有唯一的解W=W(r,λ)满足条件 (44) λ≤0≤λ,0 显然(ws(r),Rs)为(1)-(6)的稳态解当且仅当它满足如下两点边值问题: Δrws=f(ws),0 (45) (46) (47) 引进一个函数 ,,S>0 引理4 问题(45)-(47)有解(ws(r),Rs)(Rs>0)当且仅当方程F(S)=0有一个正根Rs。而且当Rs是这样的根时,(45)-(47)的解为Rs和 ,,0 (48) 证明必要性。已知Rs是(45)-(46)的解由(48)给出时,将(48)代入(47)可得F(Rs)=0。 充分性。 给定Rs>0,显然(48)是(45)-(46)的解,故若Rs是F(S)=0的正根,显然由(48)和Rs得到的(ws(r),Rs)为(45)-(47)的解。 (49) 所以式(49)成立。由介值定理可得,存在Rs>0使F(Rs)=0。 利用以上引理可得到定理2,下面将给出证明。 证明(i)由引理3和引理5易得结论。 参考文献: [1]GREENSPAN H.Models for the growth of solid tumors by diffusion [J].Stud Appl Math,1972,51: 317-340. [2]GREENSPAN H.On the growth and stability of cell cultures and solid tumors [J].Theor Biol,1976,56: 229-242. [3]CUI S.Analysis of a free boundary problem modeling tumor [J].Acta Math Sin Engl Ser,2005,21: 1071-1082. [4]FRIEDMAN A,REITICH F.Analysis of a mathematical model for the growth of tumors [J].Math Biol,1999,38: 262-284. [5]FRIEDMAN A.Mathematical analysis and challenges arising from models of tumor growth [J].Math Models Appl Sci,2007,17: 1751-1771. [6]FRIEDMAN A.Free boundary problems associated from models of tumor growth [J].Math Model Nat Phenom,2009,4(3): 134-155. [7]卫雪梅,崔尚斌.一个肿瘤生长自由边界问题解的整体存在性和唯一性[J].数学物理学报,2006,26(1): 1-8. [8]卫雪梅,崔尚斌.一个肿瘤生长自由边界问题解的渐近性态[J].数学物理学报,2007,27(4): 648-659. [9]WEI X,CUI S.Global well-posedness for a drug transport model in tumor multicell spheroids [J].Math and Computer Modelling,2007,45: 553-563. [10]NORRIS E S,KING J R,BYRNE H M.Modelling the response of spatially structured tumors to chemotherapy: drug kinetics [J].Math Comp Mod,2006,43: 820-837. [11]叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990: 115-118.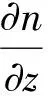
2 基本引理
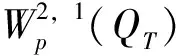
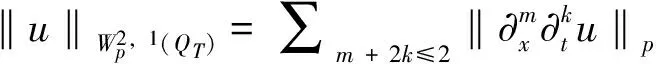
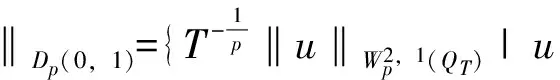
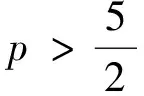
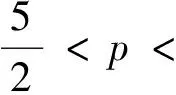
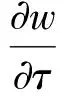
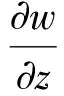
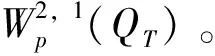
3 整体解的存在唯一性
3.1 局部解的存在唯一性
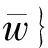
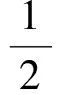
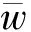
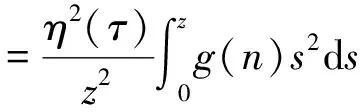
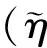
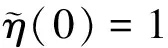
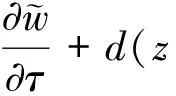
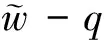
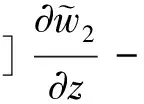
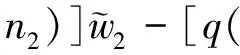
3.2 整体解的存在唯一性
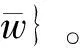
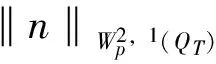
4 稳态解