基于行波模值比值与极性的选线选相法

季晨宇，袁振海，夏伟伟

（南京工业大学自动化与电气工程学院，南京211816）

小电流接地系统单相接地故障占全网故障的80% 以上，尽快选出故障线路，测定故障相，对于系统运行具有重要意义[1]。

现有的选线方法有拉路法、注入信号法、稳态信号法、暂态分量法、人工智能选线法、多原理组合算法等，主要因为接地电容电流较小不易检测，接地引起的零序电流提取受系统接地方式及系统正常运行不平衡电流等的影响，实际运行中的选线结果并不理想[2～8]。小电流接地系统发生接地故障后，将产生含有丰富故障信息的行波，利用行波选线的方法因不受中性点接地方式、过渡电阻、馈出线形式、故障时刻电压等影响克服了其他选线法的诸多不足[9]。网络中产生的多次折、反射行波不易检测识别，目前主要采用初始行波进行选线。为了使初始行波选线法更好地投入到实际运行中，一些方法被提出，文献[10]利用初始电流行波零模量判别故障线；文献[11]基于相电流初始行波模极大值幅值大小和极性选线，但未能确定故障相；文献[12]根据三个模量的故障特征选择故障相，以上三种方法需要系统安装有三相TA 或零序TA，会增加投资；文献[13]通过比较两相电流行波β、γ模量的模极大值幅值大小和极性选线定相，具体需要测量各线路A、C 相电流，据凯伦贝尔公式计算两线模量；在计算出线模量的基础上，分别对各线路的β模量与γ 模量进行大小比较，从所有线模量中找出模极大值幅值最大的3个β模量和3个γ模量，在所选模量中，含有故障线路的线模量；将所选的3个β模量与同一线路的γ 模量进行大小比较，其中的2个β模量模极大值幅值大于同一线路2个γ模量，选β模量构成选线判据，反之，选γ模量；把所选的3个判据模量进行极性比较，3个模量极性相同，表明母线故障，其中1个模量与另2个模量极性相反，这一模量所在线路为故障线路；然后，比较故障线路β、γ模量极性是相同还是相反，分别反应出是A 相还是C 相接地，β模量模极大值接近于零则表明B 相接地。此法计算量大，多重比较影响精度，判据繁琐，效率较低。

本文运用单相接地故障初始行波选线研究结果，推导β、γ 模量比值关系式，根据单相电流初始行波模极大值幅值与极性的关系，提出了一种准确有效、流程简化的选线定相方法。并通过MATLAB仿真软件验证了该法的有效性。

1 单相接地故障行波分析

1.1 各相电流初始行波分析

小电流接地系统设置C相线路经过渡电阻Rf接地，将线路看作无损耗均匀传输线来分析，如图1为C相电压源行波u1q向线路末端行进时遇故障点的传播示意图，其中Z 为线路波阻抗，u2q为折射波（即F点的电压），u1f为反射波（即F点C相初始电压行波），假设F 点对侧线路中没有反行波或对侧线路中的反行波尚未到达节点F，要决定F 点的电压u2q，根据彼得逊法则，可以将图1所示的线路化为图2所示的一个集中参数的等值电路来分析，其中ic为本侧线路上流过的电流，i′c为对侧线路上流过的电流，iR为故障支路电流。

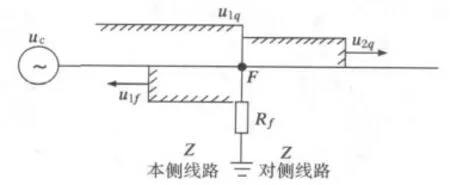
图1 入射电压u1q 在接地故障F 点的折反射Fig.1 Refraction and reflection of incident voltage u1q at the ground fault point F

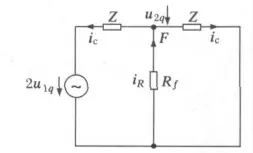
图2 彼得逊等值电路Fig.2 Peterson equivalent circuit

根据无损单导线线路波过程基本规律和电路基本定律，推导得：

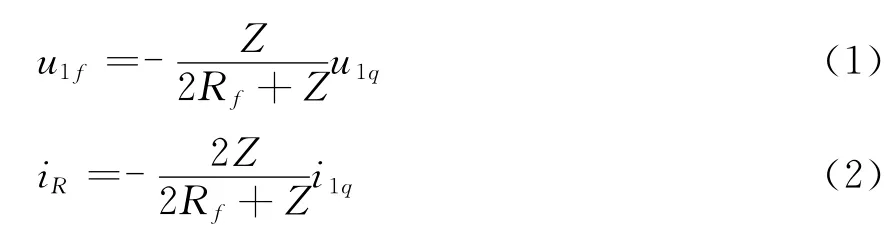
因为u2q＝u1q ＋u1f，故障支路可以用一个电压等效于u1q的电压源和一个电压等效于u1f的电压源等效，如图3所示，可见其他部分的电压和电流均保持不变。

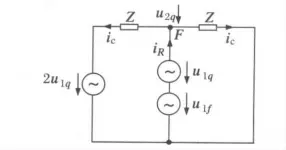
图3 替代后的等效电路Fig.3 Equivalent circuit after replacement

图3的电路可以等效为图4中两个电路的叠加，其中iR1为分电路（a）故障支路中流过的电流行波，i1为本侧线路上流过的电流行波，i2为对侧线路上流过的电流行波；iR2为分电路（b）故障支路中流过的电流行波，i3为本侧线路上流过的电流行波，i4为对侧线路上流过的电流行波。

根据电路基本定律和式（1）、（2），推导出：

式中：u1q为C相电压源行波，记作ucF；u1f为故障点C相初始电压行波，记作ucf；iR为故障支路上电流行波，记作icf，式（3）表示了故障后在故障点产生的初始电压行波、故障支路初始电流行波和故障电阻间的关系，即式（3）为故障分量的关系式。综上可以列出：

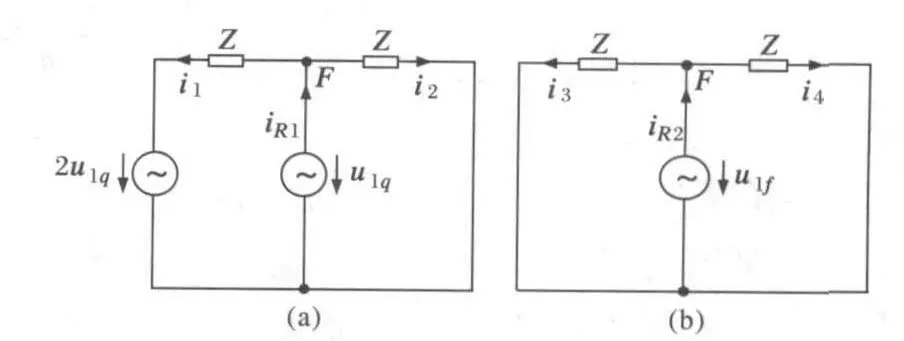
图4 分电路Fig.4 Sub－circuits

式（4）中，ibf、iaf分别为故障支路B相、A 相电流初始行波。

根据凯伦贝尔相模变换矩阵得出：

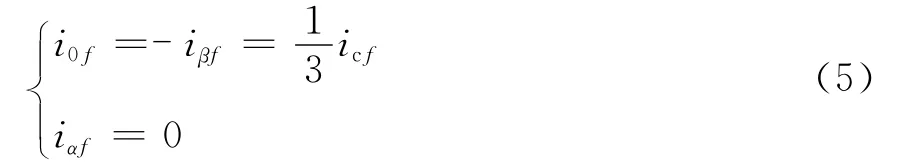
其中i0f、iαf、iβf为故障支路上各模量电流初始行波。

根据凯伦贝尔逆变换矩阵和模域欧姆定律，有式（6）、（7）：

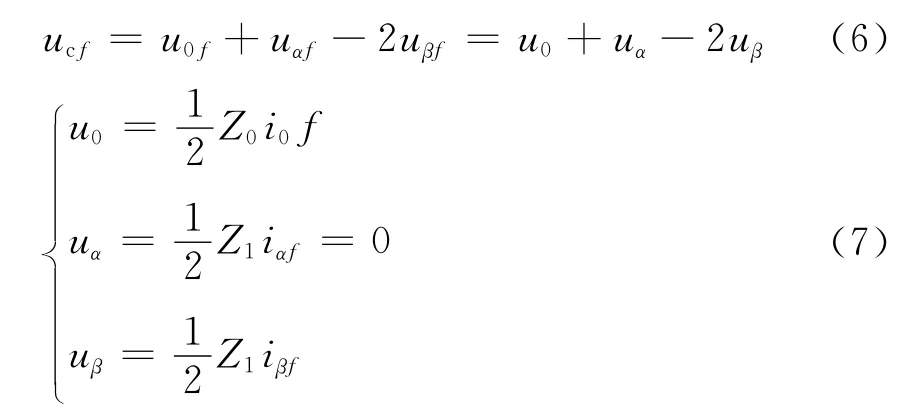
其中，u0f、uαf、uβf为故障点各模量电压初始行波，u0、uα、uβ为纯故障分量网络系统侧各模量电压初始行波，Z0、Z1分别为故障点两侧线路零模、线模波阻抗。

将式（5）、（6）、（7）代入式（4），得：

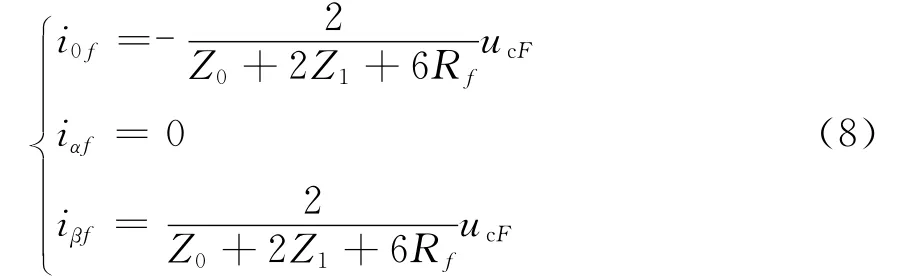
若变电站母线上接有N 回波阻抗均为Z1的线路，并且其中一回线路上发生了接地故障，故障点初始行波将向线路两侧传播，遇母线即波阻抗不连续点，行波将发生折反射，不考虑母线分布电容时，故障点初始电流行波的入射线路波阻抗为线路波阻抗，折射线路的波阻抗为非故障的N－1回线路波阻抗的并联。根据彼得逊法则，等效电路如图5。

图5中，u1q为电压初始 入射行 波，ibr、ibf、ibz分别为母线上的电流初始入射行波、反射行波和折射行波。根据图5的电路，可以列出：

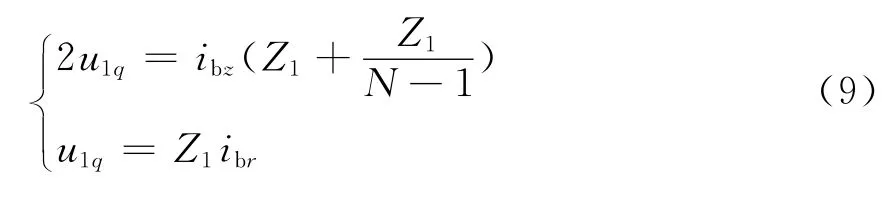
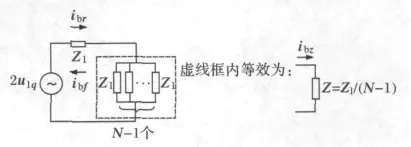
图5 行波计算等效电路Fig.5 Equivalent circuit of traveling－wave calculation

母线上的电流初始反射行波和折射行波如式（11）所示：

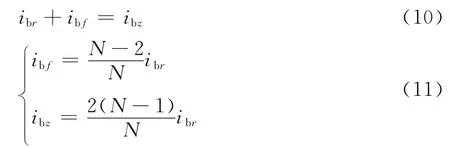
电磁波速度很快，各条线路上电流测量点与母线的距离很短，所以故障线路上测得的电流行波为入射行波和反射行波的叠加[11]，记为iLF，非故障线路上测得的电流行波为折射行波的部分，记为iLS。规定电流的正方向为由母线指向线路，因此有：

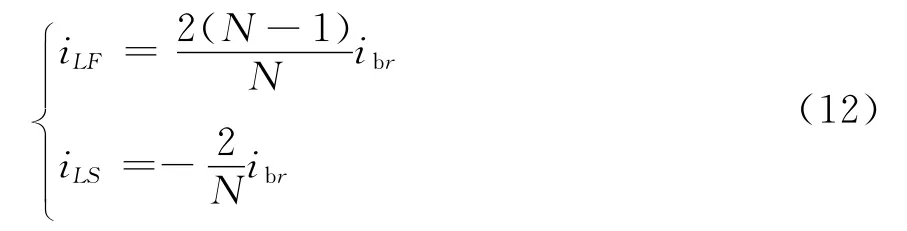
以上分析未涉及三相线路间的耦合关系，所以仅适用于相互独立的模量电气量，又因为线路上不同模量的行波速度不同，线模行波首先到达测量点，通过凯伦贝尔相模变换矩阵，可以求测量点的初始电流行波，整理如下：

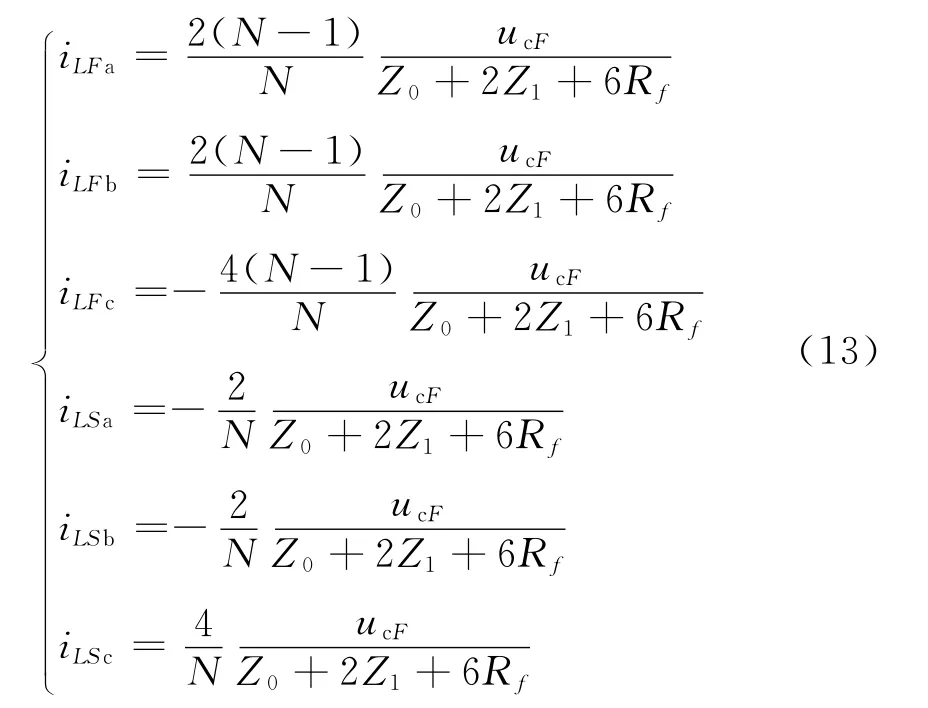
式（13）中，iLFa、iLFb、iLFc分别为故障线路a、b、c三相TA 测得的电 流初始 行波，iLSa、iLSb、iLSc分 别为非故障线路a、b、c相TA 测得的电流初始行波。对应相相比，比值关系如：

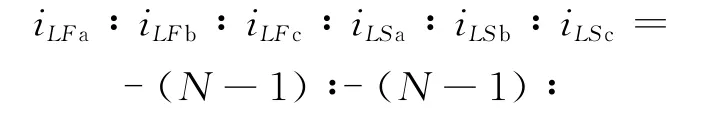
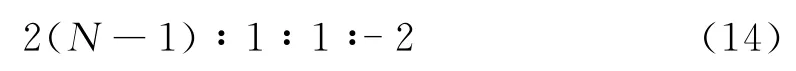
同理，可得A 相、B相分别发生接地故障的情况，如式（15）为各故障时故障线路和非故障线路对应相电流行波的比值关系式：

由式（14）、（15）可知：

1）故障线路与非故障线路的同一相电流初始行波的幅值比值等于（N－1），极性相反。

2）对故障线路而言，故障相电流初始行波幅值是非故障相电流初始行波幅值的2 倍，极性相反。两非故障相电流初始行波幅值相等，极性相同。

另外，母线故障时各线路对应相电流初始行波幅值相等，极性相同。

当考虑母线处补偿电容和对地分布电容时，可以将它们等效为一个集中总电容C[14]，行波的传播路径相当于多了一条出线，这条出线上接的是电容元件，据彼得逊法则有图6等效电路图。

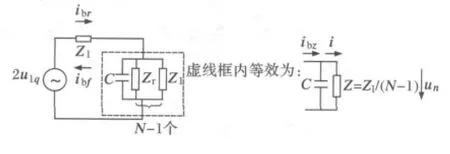
图6 考虑母线电容时行波计算等效电路图Fig.6 Equivalent circuit of traveling－wave calculation when consider the capacitance of the bus bar

可以由图6列出式（16）：

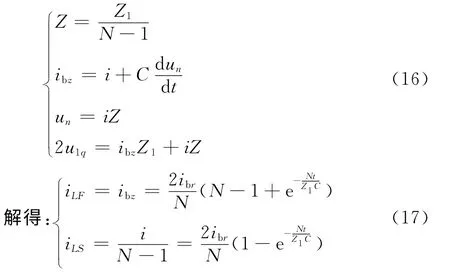
通过类比可知考虑母线电容时，故障线路与非故障线路同一相电流初始行波的比值仍为一定值，等于其值大于（N－1）。可见母线和设备的分布电容对选线判据无影响。

1.2 模量电流行波β、γ 特征分析

系统安装有三相TA 时，可以根据上节的分析结果进行选线选相，当系统安装A、C 两相TA 时，充分利用两相TA 测得的电流行波进行选线选相，更具有实用价值。由凯伦贝尔相模逆变换矩阵，有：

构造γ模分量[15]：

γ模量是由A、C两相信号求和获得，包含线模分量和零模分量，在采用初始行波选线时，首先到达测量点的行波是其中的线模分量，当线路较长时，等效采用线模进行接地选线。当C 相接地故障时，根据β、γ公式并代入式（13），有：

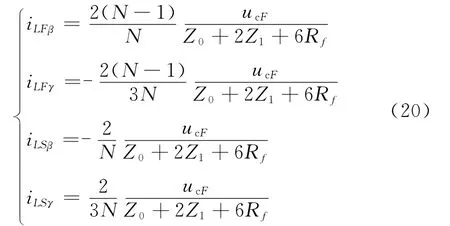
对应模量相比有：

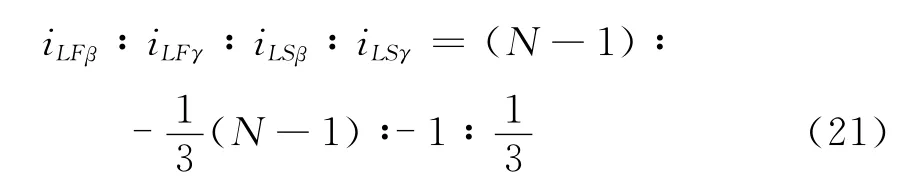
同理可得A 相、B相分别发生接地故障时，β、γ模量比例关系，如：

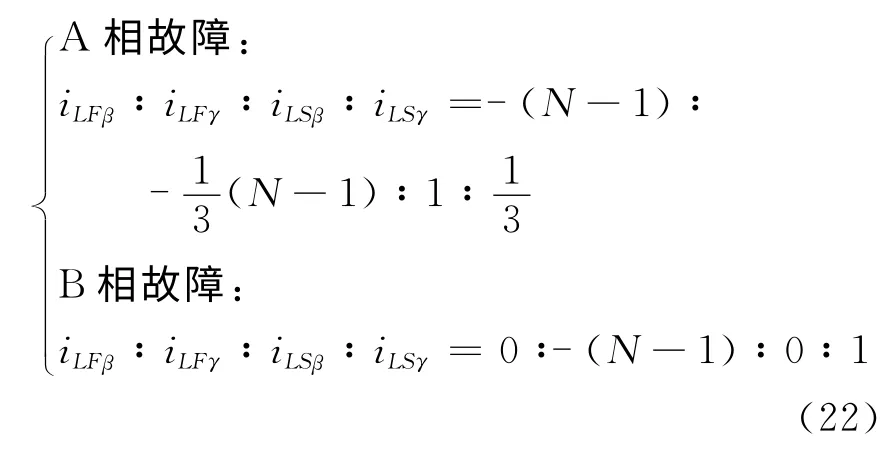
由式（21）、（22）可知：

1）故障线路与非故障线路β模量模值之比等于γ模量模值之比为（N－1），且同一线上β、γ模量极性相同还是相反，分别反应出是A 相还是C 相接地。

2）故障线路与非故障线路β模量幅值相等约为零，且故障线路与非故障线路γ模量模值之比为（N－1），极性相反，表明B相接地。

另外，母线接地时各线路β模量模值相等，极性相同，γ模量也有相同特征。

2 一种改进的选线判据

对于小电流接地系统，任何一相发生接地故障时，各相电流初始行波及其β、γ模量的模极大值有比例关系，它们的极性也有明显差异，这些差异是选线选相的依据。根据第二节的理论分析和总结，本文提出一种新型选线定相方法，该方法的原理是比较故障线路与非故障线路电流初始行波幅值和极性的相对关系，所以不受故障初相角、过渡电阻等的影响，其流程框图如图7。

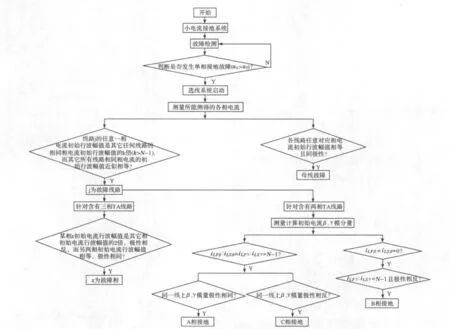
图7 选线选相流程框图Fig.7 Block diagram of fault line and phase selection

从流程图可以看出，选线系统启动后，首先计算各线路对应相相电流初始行波模极大值比值，判定故障线路；若系统安装有三相TA，比较故障线路各相电流初始行波模极大值比值和极性，选出故障相；若系统安装有两相TA，将故障与任一非故障线路的线模量模极大值比值和极性进行比较以判定故障相。

3 仿真验证

搭建四出线10kV系统，消弧线圈采用过补偿接地方式，补偿度为10%，线路参数如下：变压器110／10kV，正 序 参 数：R1＝0.48 Ω／km，L1＝0.9337mH／km，C1＝0.01274μF／km，零序参数：R0＝0.79 Ω／km，L0＝4.2146 mH／km，C0＝0.007751μF／km；4条出线的长度分别为：L1＝50 km；L2＝75km；L3＝80km；L4＝100km。设置线路2上距离母线25km处发生A相经100Ω电阻接地故障，本文采用MATLAB 软件进行仿真计算[16]，初始行波信号持续时间很短，需要在极短的时间内采集足够多的信号，这就要求较高的采样频率，这里取采样频率为1 MHz；另外，行波信号的精准捕捉和判别是影响选线选相可靠性的重要因素，使用小波变换可以准确检测故障的初始行波波头，利用多分辨率分析，可以有效消除噪声，这里用B样条小波对行波信号进行三个尺度的变换[17]。如图8（a）所示为各线路A相电流初始行波在22尺度下的B样条小波变换的模极大值波形，从图中可以看出线路2初始模极大值与1、3、4线路初始模极大值比值均为4.8，大于3，线路1、3、4的A 相电流初始行波模极大值比值为1（对于另外两相情况一样），根据判据流程可以判定线路2为故障线路。针对含有三相TA 线路，线路2的三相电流初始行波模极大值波形如图8（b）所示，可以看出A 相电流初始行波幅值是其它相电流初始行波模极大值的两倍，极性相反，而B、C相电流初始行波模极大值相等，极性相同，因此可以判定A 相为故障相。针对含有两相TA 的线路，线路1和2模量行波β、γ的模极大值如图8（c）所示，可以看出线路2与线路1模量行波β的模极大值幅值之比约为3，且线路2上两模量行波的极性相同，可以判定A 相接地。采用同样的方法，根据23、24尺度下的小波变换模极大值，可以得到相同的结论，最后，根据以上3个尺度的结果，采用3取2的选择原则保证最终结果的准确性和可靠性，确定线路2的A相发生接地故障。

其它故障分析同上，限于篇幅不再赘述。仿真算例结果表明，相比较β、γ 模量行波选线法，本方法计算量大大缩小，步骤简化，避免了多重比较带来的误差，提高了故障选线选相的速度与准确度。

若要完成本算法的开发应用，应该考虑3点：①因为本文的选线选相方法利用的是线模初始行波，所以装置必须在零模初始行波到达之前，正确识别出线模初始行波，为了避免零模初始行波与线模初始行波发生混叠，应提高装置的采样频率，以缩小选线死区[11]；②高采样频率对保护的硬件系统的CPU、内存开销和系统电磁兼容性要求较高[18]；③为了精准捕捉和判别行波信号，可以结合高响应速度和高保真的数据采集与处理硬件，如数字信号处理DSP（digital signal processing）技术与新型光传感器。

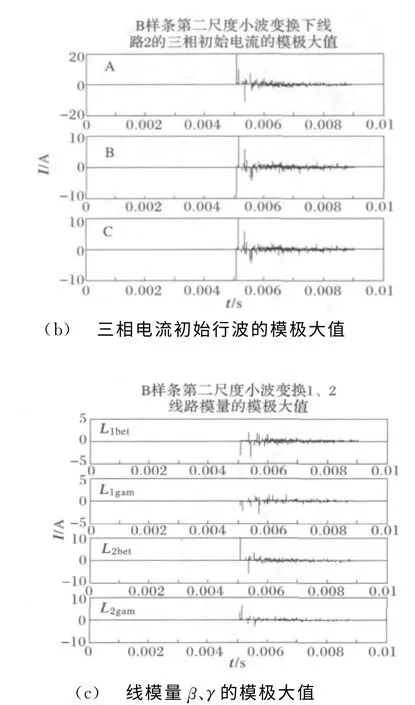
图8 初始电流行波和模量的小波变换和模极大值Fig.8 Wavelet transform and modulus maxima of current initial traveling wave and modulus

4 结语

本文在对小电流接地系统单相接地故障电流初始行波分析的基础上，推导β、γ 模量比值关系式，将时域行波和线模量相结合，提出了基于行波模值与极性的选线选相法，算法简洁明了，通过判定相电流初始行波及两模量模极大值比值和极性，能更快更准选线选相，适用于现场在线分析；完善了选线定相流程，使之适用于装有两相或三相TA的系统，不需要增加资金投入。

[1]Zhao Chengyong，Guo Yanfen，Li Gengyin.The similitude power detection on single－phase－to－ground fault in the non－solidly grounded system[C]／／IEEE／PES Transmission and Distribution Conference and Exhibition，Dalian，China：2005.

[2]肖白，束洪春，高峰（Xiao Bai，Shu Hongchun，Gao Feng）.小电流接地系统单相接地故障选线方法综述（Survey of the methods of fault line selection for single－phase－to－earth fault in networks ungrounded neutral）[J].继电器（Relay），2001，29（4）：16－20.

[3]黄芳，陈志军，蒋晓宇（Huang Fang，Chen Zhijun，Jiang Xiaoyu）.小电流接地系统故障选线算法综述（Survey of algorithms of fault line selection in power system with indirectly grounded neutral）[J].江苏电机 工 程（Jiangsu Electrical Engineering），2005，24（3）：80－84.

[4]李冬辉，史临潼（Li Donghui，Shi Lintong）.非直接接地系统单相接地故障选线方法综述（Survey of the methods to select single－phase fault line in neutral point indirectly grounded power system）[J].继电器（Relay），2004，32（18）：74－78，84.

[5]徐丙垠，薛永端，李天友，等（Xu Bingyin，Xue Yongduan，Li Tianyou，et al）.小电流接地故障选线技术综述（Review of line selection of grounding fault in non－effectively grounding network techniques）[J].电力设备（Electrical Equipment），2005，6（4）：1－7.

[6]傅周兴，万耕（Fu Zhouxing，Wan Geng）.小电流接地系统单相接地故障选线方法（Methods of fault line selection for single phase to earth fault in networks with ungrounded neutral）[J].低压电器（Low Voltage Apparatus），2002，（3）：43－47.

[7]张宏艳，张承学，熊睿，等（Zhang Hongyan，Zhang Chengxue，Xiong Rui，et al）.国内外几种先进的小电流接地系统单相接地故障选线方法分析与比较（Analysis and comparison of several advanced fault line selective methods in small current grounding power system）[J].电力建设（Electric Power Construction），2005，26（11）：41－44，50.

[8]张树文，李文毅，米增强，等（Zhang Shuwen，Li Wenyi，Mi Zengqiang，et al）.小电流接地系统单相接地保护原理和技术综述（Survey of Protective Principle and Technique in Distribution System with Neutral Non－effective Grounding）[J].电力情报（Information on Electric Power），1994，（2）：1－4.

[9]董新洲，毕见广（Dong Xinzhou，Bi Jianguang）.配电线路暂态行波分析和接地选线研究（Analysis on transient traveling wave and study on fault line selection for distribution lines）[J].中国电机工程学报（Proceedings of the CSEE），2005，25（4）：1－6.

[10]黄景光，刘会家，胡汉梅，等（Huang Jingguang，Liu Huijia，Hu Hanmei，et al）.行波小波系数极大值极性法接地故障选线研究（Distribution grid earth fault line detection study by traveling wave wavelets coefficient maximum polarities）[J].高 电 压 技 术（High Voltage Engineering），2006，32（8）：100－104.

[11]施慎行，董新洲（Shi Shenxing，Dong Xinzhou）.基于单相电流行波的故障选线原理研究（Study of fault line selection using single－phase current traveling waves）[J].电力系统保 护与控制（Power System Protection and Control），2008，36（14）：13－16.

[12]乔峰（Qiao Feng）.基于小波理论的10kV 配电线路暂态行波故障选相研究（Research of 10kV distributed line fault phase selections with transient current travelling waves and wavelet transform）[J].科技信息（Science ＆Technology Information），2008，（16）：648－650.

[13]毕 见 广，董 新 洲，周 双 喜（Bi Jianguang，Dong Xinzhou，Zhou Suangxi）.基于两相电流行波的接地选线方法（Fault line selection based on two－phase current traveling wave）[J].电力系统自动化（Automation of Electric Power Systems），2005，29（3）：17－20，50.

[14]周登登，刘志刚（Zhou Dengdeng，Liu Zhigang）.基于电容器投切的复小波选线方法（Line selection method based on capacitor switching by complex wavelet）[J].四川电力技术（Sisuan Electric Power Technology），2009，32（1）：13－17，27.

[15]丁瑾，袁振海（Ding Jin，Yuan Zhenhai）.10kV 配电线路单相接地故障暂态电流行波选线研究（Study on line selection of 10kV distributed line single－phase earth fault with transient current traveling wave）[J].电测与仪表（Electrical Measurement ＆Instrumentation），2009，46（4）：29－34，38.

[16]张德丰.Matlab小波分析与工程应用[M].北京：国防工业出版社，2008.

[17]张兆宁，董肖红，潘云峰（Zhang Zhaoning，Dong Xiaohong，Pan Yunfeng）.基于小波变换模极大值去噪方法的改进（Improved algorithm based on modular maximum denosing method by wavelet transformation）[J].电力系统及其自动化学报（Proceedings of the CSU－EPSA），2005，17（2）：9－12.

[18]胡汉梅，黄景光，刘会家（Hu Hanmei，Huang Jingguang，Liu Huijia）.基于小波分析的行波相位比较法接地故障选线（Grounding failure detection by comparing phases of traveling wave wavelets coefficients）[J].高电压技术（High Voltage Engineering），2007，33（12）：168－172.