分布式电源优化配置的仿电磁学算法

王学友，周步祥，付 锦，林 楠，孙京锋，刘金华

（1.四川大学电气信息学院，成都610065；2.四川电力职业技术学院，成都610071；3.二滩水电开发有限责任公司，成都610051）

近年来，随着人们对传统集中供电模式的重新思考，认识到分布式发电具有灵活、分散、小型、靠近用户和合理使用清洁能源的特点，能提高局部供电可靠性、减少输电损耗、提高一次能源的利用率及减少废气排放，具有良好的应用前景[1]。综合考虑分布式电源DG 的运行效益时，一方面需提高电网的可靠性，另一方面需尽量降低DG 的配置成本，同时也要考虑降低电网的线损率。DG 的位置和容量对电网网络可靠性，短路电流，线路潮流，节点电压等都会带来不同程度的影响[2～4]，因此，DG的选址和定容十分重要。

一些文献已经对DG 的安装地点和容量的优化配置进行了研究。如：DG 成本最低以一定可靠性指标为优化目标进行优化配置[5]；DG 容量已知情况下运用解析法确定最优的DG 规划方案[6]；运用禁忌搜索法在DG总容量已知的情况研究DG的位置和容量的确定[7]；运用C语言开发软件进行优化得到配电网中个DG 的优化配置[8]；利用粒子群优 化 POS 和 演 化 规 划 EP（evolutionary programming）算法寻找网损最小、可靠性最高的DG 优化方案[9]。

本文主要研究在不同DG 的容量已知情况下，建立考虑安装成本、供电可靠性、线损率的多目标函数模型，并将多目标函数归一化和加权处理，建立以最小化配电网耗费作为优化目标函数，采用仿电磁学算法，得到不同DG 在不同地点的最优规划方案。通过与遗传算法的比较，该算法在快速性、准确性和高容错性方面具有明显的优势。

1 优化目标

2 仿电磁学算法

2.1 基本原理

2003年，美国北卡莱纳州州立大学博士Birbil提出新型随机全局优化算法—— 仿电磁学算法ELM（electromagnetism－like mechanism）[12，13]。该算法通过模拟带电电荷间吸引和排斥机理来确保优化问题种群的多样性和搜索空间的完整性，用总矢量力的计算来确定种群的移动速度，根据种群进化模型来确定种群的进化方向，采取局部搜索提高算法的邻域搜索能力，当满足收敛条件时输出优化问题的解。仿电磁学运行的前提和基础是在该阶段确定种群的规模、变量的维数及初始解的分布规律，采用均匀随机方法确定初始种群，并将每个个体看作一个带电粒子。采用电荷模拟来描述种群中个体与当前代最优个体之间的接近程度，其值越大表明越接近最优解，其值越小与最优解的距离越大，该过程是计算总矢量力的前提和基础。电荷模拟的数学模型为

ELM 算法根据粒子及其电荷值来描述种群中每个带电粒子的矢量力和性质。总矢量力计算的主要作用是确定种群间作用力的性质及种群移动的程度，在一定程度上影响着算法的全局搜索范围，其数学模型为

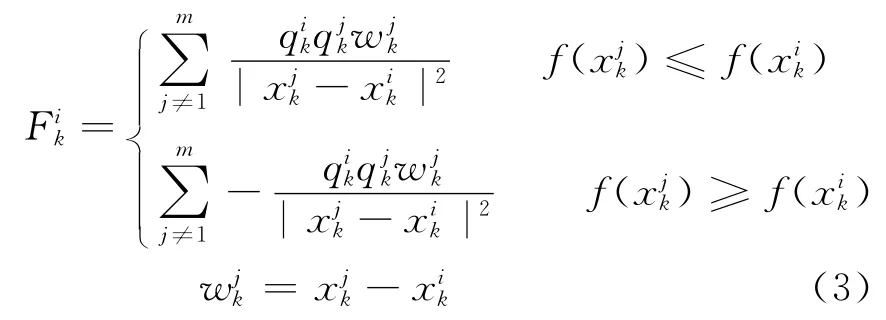
种群移动是确定新一代种群不可缺少的步骤，它是保证算法继续进化和种群多样性的必备条件，其作用类似于遗传算法的交叉和变异算子，其种群进化数学模型表示为：

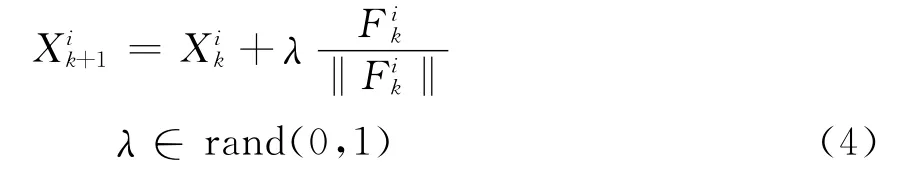
2.2 算法改进

2.2.1 初始种群

本研究在前人研究的基础上，设计已知、固定的培养基作为满足冠突散囊菌生长需要的特定基质，并以高纯度咖啡碱、可可碱和茶碱作为冠突散囊菌液体发酵培养的唯一外源添加底物，考察冠突散囊菌对上述3种单体成分为期10 d的发酵特性，为进一步丰富茯茶品质形成机理提供理论依据。

通过均匀随机数的产生方法，产生一个m×n的矩阵A（m 个种群个体，n个变量）对A 进行取整处理，将其转化为整数矩阵A。处理的方法为：若Xi，j＞0.5，Xi，j的取值为1，否则Xi，j的取值为0。由于初始矩阵产生采用的是均匀随机方法，处理时采用的是以0.5等概率选择为界，能够继续保持种群的均匀性和多样性。

2.2.2 总矢量力模型

当种群中出现个体相同的情况时，将造成总矢量力模型中出现分母为零的情形，结果造成矢量力趋向无穷大，从而使算法无法进行，因此需要对式（3）进行适当处理，具体方法是在式（3）的分母上加一个抗干扰条件aδ，改进后的总矢量力模型为

式中：aδ是一个大于零的数。通过分析可知，这种改进不仅可以避免分母为零的情形，同时不改变电荷的受力性质，所以该模型仍然符合仿电磁学算法的基本思想。

2.2.3 变量离散化及越界处理

种群移动公式和局部搜索公式在计算时，不满足变量的取整离散条件，因此，需要对新解进行处理以使优化结果满足实际要求。

式中：δ为0～1 的随机数，M 为搜索步长，为大于零的数。针对不满足离散取整条件，采用方法：种群中每个解元素的小数部分按四舍五入转化为整数；针对越界情况，若超出上界，将其解元素取为上界，若超过下界，将其解元素取为下界。

仿电磁学算法采用的是等概率搜索，上述的处理变量越界的方法并不违背仿电磁学算法的基本原则，处理过程始终保持等概率搜索的处理方法。经过处理之后不仅可以满足决策变量的约束条件及其离散化特性，同样保持了种群的多样性，有利于找到优化问题的全局最优解。

2.2.4 收敛条件

在仿电磁学基本算法中，采用指定的最大迭代次数作为终止条件，很显然这种收敛条件具有很大的缺陷，采用的迭代次数太多，将降低算法的效率，若采用的迭代次数太小，可能造成输出解不是问题的最优解，引起分布式电源优化配置不准确，影响电网的经济运行。因此，本文采用算法的停滞代数作为收敛条件。

2.3 基本求解步骤

基本求解步骤如图1所示。

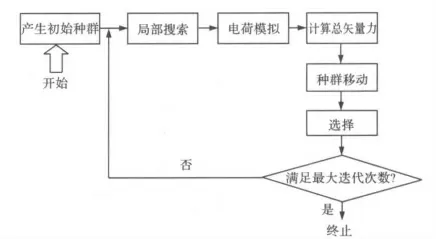
图1 仿电磁学算法的流程图Fig.1 Flow chart of ELM

3 算例分析

3.1 算例描述

采用如图2所示的放射状结构的配电网中，进行优化方法的测试。在系统中线路距离l1＝l2＝l3＝l4＝l5＝l＝6km，配电源与当地负荷的距离可以忽略，配网中总负荷为5.25 MW，节点2～6所带的负荷分别为0.5 MW，1.25 MW，2.25 MW，0.25 MW，0.5 MW。原配电网的指标为：ASAI＝99.75%，ΔA ＝7.36%。各种DG 在各个点的配置成本如表1和表2。

图2 测试系统结构图Fig.2 Structure drawing of test system

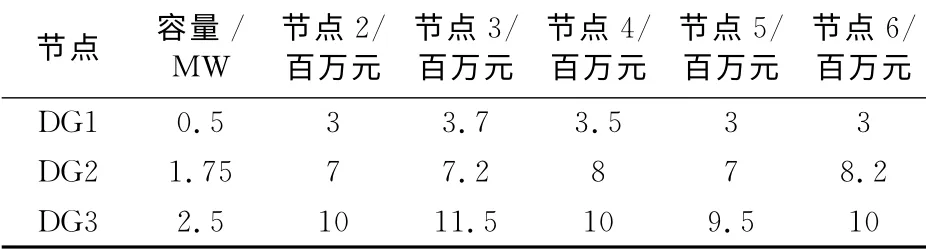
表1 不同DG 在各节点的配置成本Tab.1 Configuration costs of different DGs in different nodes

仿真时，设配网负荷全部由DG 供电，不考虑负荷备用。设置Tmax为3500h，a为0.7元／（kW·h）。

表2 不同节点的户数及停电时间Tab.2 User number of different nodes and power cutting off time

3.2 仿真结果与比较

仿真时，分别采用仿电磁学算法和遗传算法（GA）共同求解，对分布式电源的配置结果和工作效率进行比较。分别对配置成本、可靠性、线损率的目标函数赋予不同权重系数，列举4种情况讨论。

当考虑配置成本、可靠性、线损率的重要性为一样时，可赋予权重系数ω1＝ω2＝ω3＝0.33。采用ELM 算法的结果是：DG配置地点分别为节点4配置DG3、节点5配置DG2、节点6配置DG1，电网耗费F 为2153万元，DG配置投资为2000万元，可靠性为99.80%，线损率为0.99%；采用GA 算法的结果是：DG配置地点分别为节点2配置DG2、节点4配置DG3、节点5 配置DG1。电网耗费F 为2172万元，DG 配置投资为2000 万元，可靠性为99.80%，线损率为1.13%。

当考虑配置成本更低，可靠性、线损率的重要性一样时，可赋予权重系数ω1＝0.8、ω2＝ω3＝0.1。采用ELM 和GA算法结果都是：DG配置地点分别为节点2配置DG2、节点5配置DG3、节点6配置DG1，电网耗费F 为2208 万元，DG 配置投资1950万元，可靠性为99.93%，线损率为1.99%。

当考虑可靠性更高，配置成本、线损率的重要性一样时，可赋予权重系数ω2＝0.8、ω1＝ω3＝0.1。采用ELM 算法的结果是：DG 配置地点分别为节点2配置DG1、节点5配置DG2、节点6配置DG3，电网耗费F 为2203 万元，DG 配置投资为2000万元，可靠性为99.98%，线损率为1.56%；采用GA 算法的结果是：DG 配置地点分别为节点2配置DG2、节点5配置DG3、节点6配置DG1，电网耗费F 为2208万元，DG配置投资1950万元，可靠性为99.98%，线损率为1.99%，当考虑线损率更低，配置成本、可靠性的重要性一样时，可赋予权重系数ω3＝0.8、ω1＝ω2＝0.1。采用ELM 和GA算法的结果都是：DG 配置地点分别为节点3 配置DG2、节点4配置DG3、节点6配置DG1。DG 配置投资2080万元，可靠性99.76%，线损率0.43%。

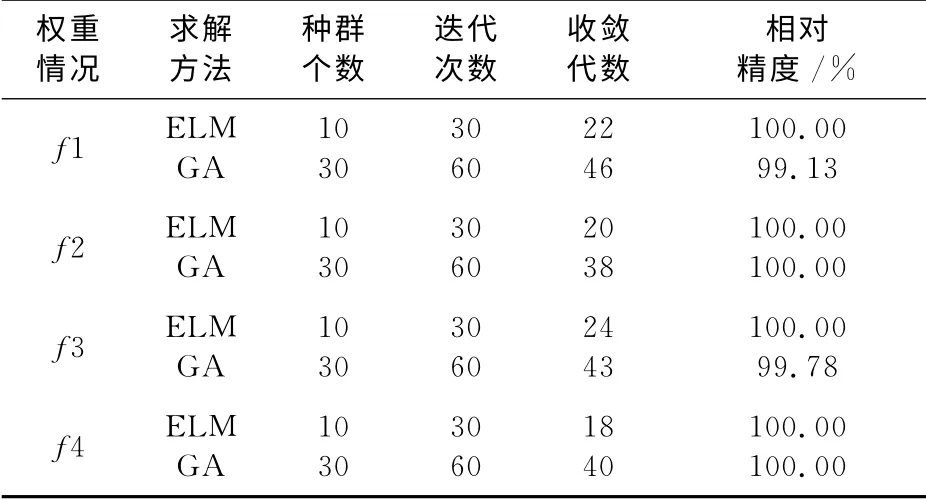
表3 不同仿真方法性能比较Tab.3 Performance comparison of different algorithms in simulation

由仿真结果和仿真方法性能比较可知，分布式电源实现优化配置，运用ELM 算法只需要较少的种群个数和迭代次数。当遗传算法的种群个数设定为30个，迭代次数设定为60时，仍然具有较高的误判率；而当ELM 算法初始种群个数为10，迭代次数为30时，其相对精度仍然高于遗传算法，具有更高的容错能力。通过Matlab编程运行，ELM算法在分布式电源优化配置的容错性能和运行效率方面，具有明显优势。

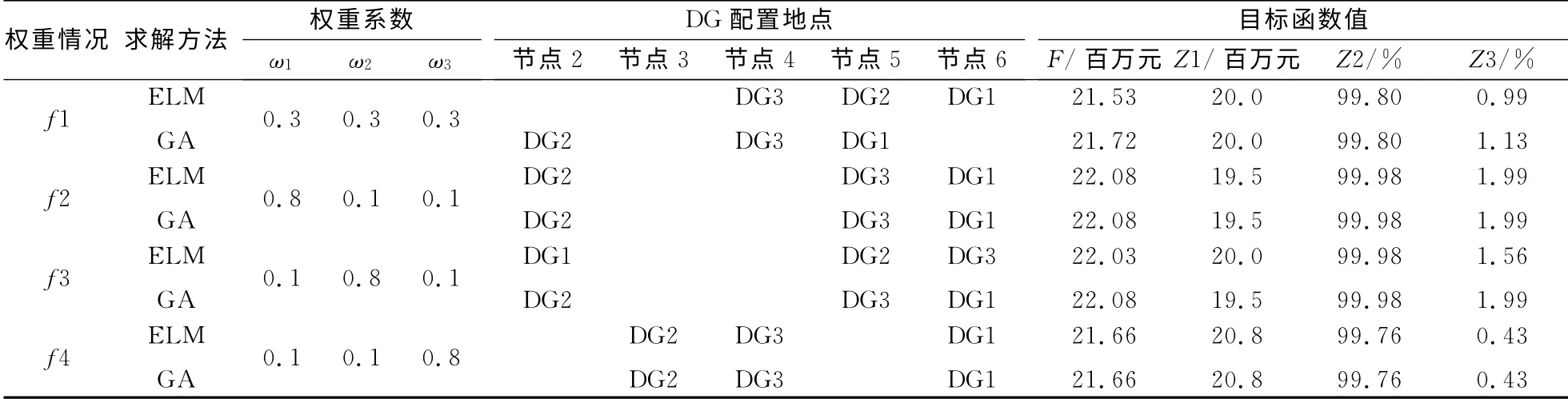
表4 不同权重系数仿真结果Tab.4 Simulation results of different weight coefficients

4 结论

1）目标函数的构造最终决定着DG 优化配置的准确性，利用归一化本文把可靠率考虑是减少收益的函数，将降低的网络损耗转化为节省的购电成本。将DG 配置成本最低、可靠性最高、线损率最低转化成目标函数最小化配电网耗费。

2）仿电磁学算法通过模拟电荷间作用力特性及其等概率选择思想，保证种群的多样性，提高算法提前收敛的抗干扰性，相对于遗传算法其原理简单、求解效率高、容错性高。

3）本文考虑不同类型DG 在不同安装地点的优化配置，对于未来配电网中分布式电源的规划具有一定研究意义。

[1]Basso Thomas S，DeBlasio Richard.IEEE 1547series of standards：interconnection issues[J].IEEE Trans on Power Electronics，2004，19（5）：1159－1162.

[2]Barker Philip P，De Mello Robert W.Determining the impact of distributed generation on power systems：Part 1－Radial distribution systems[C]∥IEEE Power Engineering Society Transmission and Distribution Conference，Seattle，USA：2000.

[3]Ijumba N M ，Jimoh A A，Nkabinde M.Influence of distribution generation on distribution network performance[C]∥IEEE AFRICON Conference，Cape Town，South Africa：1999.

[4]王志群，朱守真，周双喜，等（Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，et al）.分布式发电对配电网电压分布的影响（Impacts of distributed generation on distribution system voltage profile）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（16）：56－60.

[5]邱晓燕，夏莉丽，李兴源（Qiu Xiaoyan，Xia Lili，Li Xingyuan）.智能电网建设中分布式电源的规划（Planning of distributed generation in construction of smart grid）[J].电网技术（Power System Technology），2010，34（4）：7－10.

[6]Griffin T，Tomsovic K，Secret D，et al.Placement of dispersed generation systems for reduced losses[C]KB∥Hawaii International Conference on System Sciences，Maui，USA：2000.

[7]Nara Koichi，Hayashi Yasuhiro，Ikeda Kazushige，et al.Application of tabu search to optimal placement of distributed generators[C]∥IEEE Power Engineering Society Transmission and Distribution Conference，Columbus，USA：2001.

[8]Agalgaonkar A P，Dobariya C V，Kanabar M G，et al.Optimal sizing of distributed generators in microgrid [C]∥IEEE Power India Conference，New Delhi，India：2006.

[9]Basu A K，Bhattacharya A，Chowdhury S P，et al.Reliability study of a micro grid system with optimal sizing and placement of DER[C]∥CIRED Seminar：SmartGrids for Distribution，Frankfurt，Germany：2008.

[10]郭永基.电力系统可靠性分析[M].北京：清华大学出版社，2003.

[11]张勇，吴淳（Zhang Yong，Wu Chun）.分布式发电机在配电网中的优化配置（Optimal placement of DG unit in distribution system）[J].电力系统保护与控制（Power System Protection and Control），2010，38（11）：33－37，43.

[12]Birbil S Ilker，Fang Shu－Cherng.An electromagnetism－like mechanism for global optimization[J].Journal of Global Optimization，2003，25（3）：263－282.

[13]郭壮志，吴杰康（Guo Zhuangzhi，Wu Jiekang）.配电网故障区间定位的仿电磁学算法（Electromagnetismlike mechanism based fault section diagnosis for distribution network）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（13）：34－40.