独立分量分析在谐波源辨识中的应用

郑东方，陈红坤，杨志平

（武汉大学电气工程学院，武汉430072）

自从采用交流电作为电能输送的一种方式起，人们就已经意识到电力系统中存在的谐波问题。近年来随着社会经济的快速发展，大量的电力电子非线性设备接入电力系统中，使电力系统受到严重的污染，谐波问题更加突出。另外，随着低碳经济时代的到来，国家大力开发风能以及太阳能等清洁资源，并将风电、光伏发电与传统电网并网，使得系统中的谐波情况更加复杂，这些对电力系统的安全、稳定运行造成了极大的危害。如何有效地对谐波进行控制并确定谐波污染责任和治理责任，已成为电力系统和用户共同关注的问题，而控制和改善谐波的前提就是对谐波源进行准确辨识[1]。

目前，电力系统中的典型谐波源，就其非线性特性而言有三类[2]：铁磁饱和型，包括各种铁芯设备，如变压器、电抗器等，其铁磁饱和特性呈现非线性，这种铁芯的非线性磁化特性将引起谐波；电子开关型，主要为各种交直流换流装置、双向晶闸管可控开关设备以及脉冲宽度调制PWM（pulse width modulation）变频器等电力电子设备；电弧型，交流电弧炉和交流电焊机等。

谐波源辨识最初是作为谐波潮流的逆问题提出的[3]。即通过测量电网中线路的谐波电流和部分节点的谐波电压，采用状态估计的方法计算负荷注入电网的谐波功率，当注入的谐波功率为正时，则判定该负荷为谐波源。此外，瞬时功率理论也被运用于谐波源辨识研究当中，通过三相系统中特定节点处的滤波装置数据得到系统谐波的瞬时有功功率，来辨识电网中主要的谐波源。另外，有很多新的算法如线性神经网络等被应用于谐波状态估计中[4]，并在此基础上开发了相应的程序和装置用于实际电网中谐波源的辨识。另一类辨识谐波源的方法是通过研究电流波形和电压波形之间的联系，找出相应的负荷参数作为判定谐波源的指标。以上这些研究主要集中在状态估计方法的基础上，目的是利用尽可能少的测量装置取得令人满意的辨识效果，对于谐波源辨识的判据并没有提出新的观点。

独立分量分析ICA（independent component analysis）是近年来发展起来的一种高效的盲源分离方法，描述了对未知源信号的估计重现过程，也可以作为一种抽取独立信号源的技术，已在特征提取、语音识别、生物医学信号处理、通信等领域受到广泛关注[5～7]。本文将电力系统谐波辨识的问题抽象为盲源分离问题，从而将独立分量分析应用于谐波辨识。和一般的盲源分离问题不同的是，基于对谐波干扰的先验知识有一定的了解，因而处理起来比较容易。本文以交流电弧炉和饱和变压器为例在Matlab软件中进行仿真。仿真结果表明，基于独立分量分析的谐波辨识法具有很高的精度和抗噪性能。

1 独立分量分析法

1.1 基本原理

独立分量分析是盲源分离方法的一个重要分支，其主要思想是在对源信号及其传输通道均未知的情况下，使分离出来的独立分量最大程度地逼近各个源信号，即建立目标函数以寻优来实现逼近。其简单原理框图如图1所示。

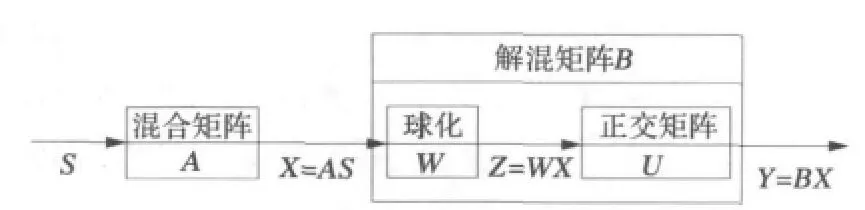
图1 ICA的简单框图说明Fig.1 Simple diagram shows of ICA

其中S ＝[s1，s2，…，sn]T是相互独立的源信号，X＝[x1，x2，…，xm]T是观测信号，每个观测信号均由源信号线性加权得到，即：

式中A是m×n的混合矩阵，A和S 均未知，利用中心极限定理，即当多个相互独立的随机变量具有有限的均值和方差时，则不论这些随机变量服从何种分布，其和形成的随机变量必近似服从高斯分布。由上式知，xi比si更接近高斯分布，换句话说，si比xi有更强的非高斯性。在分离的过程中通过测量si的非高斯性，当si的非高斯性度量达到最大时，则说明源信号从观测信号中分离。ICA 的方法正是通过对各独立量进行非高斯性度量，采用某种优化方法求解混矩阵B，并令

使Y 尽可能的逼近S。有时解混过程又可以分为两步—— 球化W 和正交变换U，球化的目的是使输出Z的各分量的方差为1，而且互不相关；正交变换的目的是使输出Y 的各分量的方差保持为1，同时使其各分量尽可能独立。由于Z中的各分量已经满足独立性对二阶统计量的要求，因此正交变换时只需考虑三阶以上的统计量，使算法得到很好的简化。

对于式（1），通常有以下3点约束：（1）源信号S 是统计独立的；（2）源信号S 中至多有一个是服从高斯分布的；（3）观测信号的个数不小于源信号的个数。

由上述分析可知，ICA 的主要任务是：首先建立以分离信号的独立性为量度的目标函数，目前常用的目标函数有互信息、负熵、似然函数等[7]；其次是寻找优化算法使目标函数取得极值，常用的算法有极大峰度法、自适应算法、探查性投影追踪法等[8]。本文将采用基于负熵的ICA 固定点算法：FastICA 算法。

随机向量y 的负熵定义为

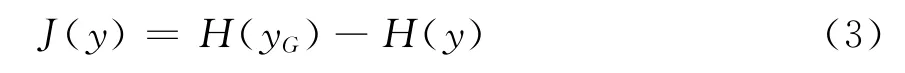
式中yG为与y 具有相同的均值及方差的高斯分布的随机向量；H（y）为概率密度为p（y）的向量y的信息熵：

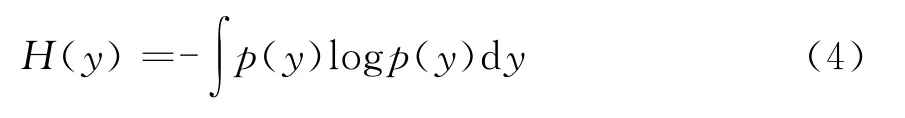
由信息论的知识可知，在同方差的情况下，高斯信号具有最大的信息熵，所以负熵的值总是非负的，可以用来作为随机向量非高斯量的度量。由于p（y）很难求出，所以无法计算出式（1.3）中的负熵J（y），从而无法判断信号的非高斯性。负熵可以近似表示成下式[9]：

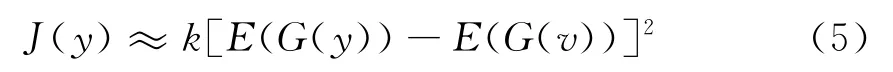
式中：k是正的常量；E（·）为均值运算；v是一个与y 具有同均值同方差的高斯随机向量。G（y）通常可取以下形式的函数：

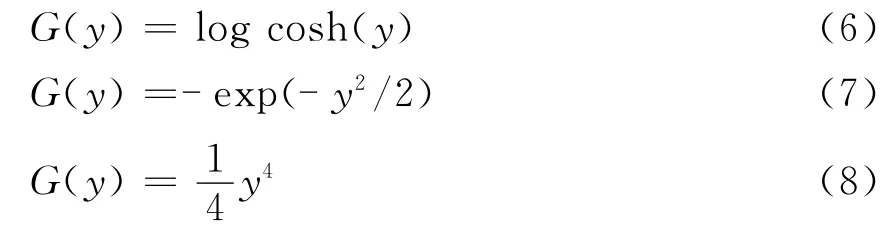
以式（5）为目标函数，应用FastICA 算法，通过迭代过程来调整B，使J（y）达到最大，收敛后可使Y 尽可能的逼近S。

1.2 Fast ICA算法的步骤

采用负熵作为判据时，由式（5）及yi＝Z得：

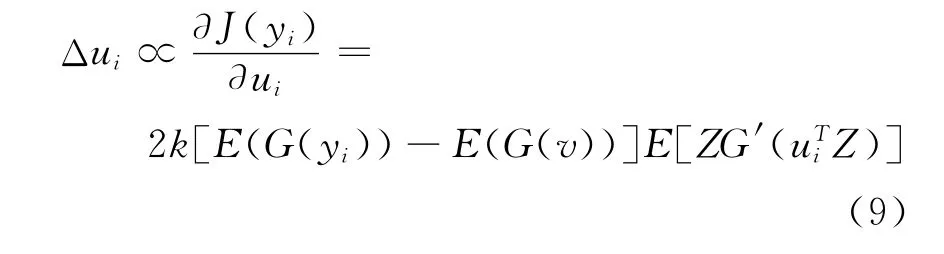
稳态时Δui＝0，由此得到固定点迭代的两步算式[10]：

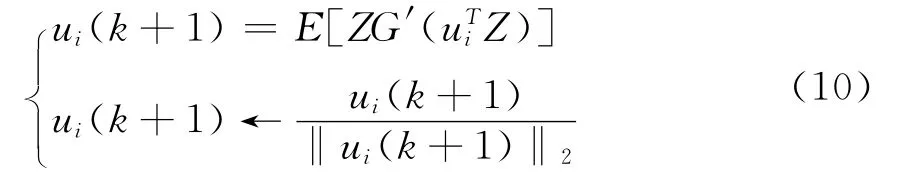
由于第二步中有归一运算，所以第一步中的系数可以省略。为了改进该算法的收敛性能，用牛顿迭代算法，并将上式等效地表示为[11]：

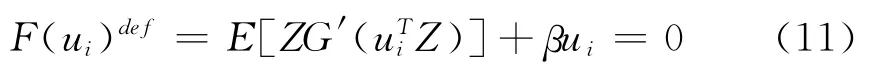
用牛顿迭代法求解，得：

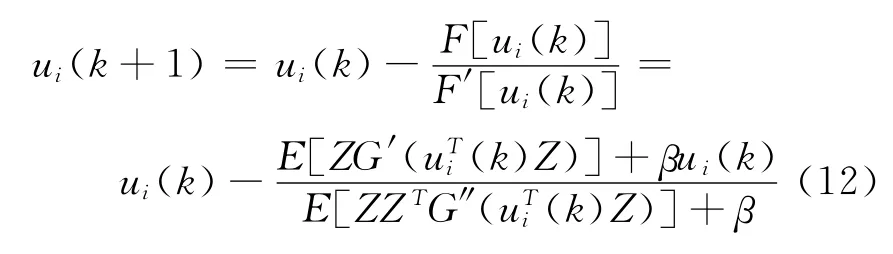
由于Z是球化数据，再对上式进行通分简化整理得：

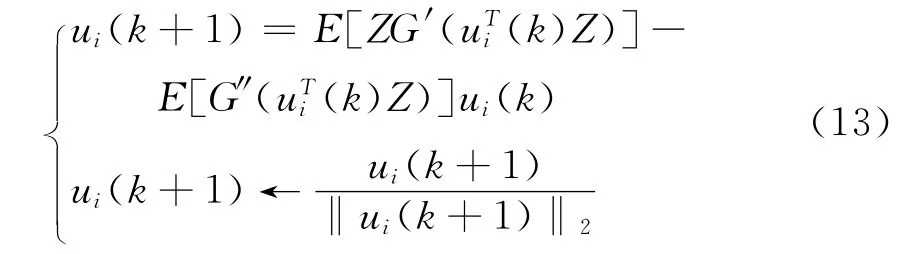
总而言之，采用负熵的固定点算法的步骤可总结如下：

（1）将X 去均值，然后通过球化得到Z；

（2）任 意 选 择ui的 初 值ui（0）， 满 足‖ui（0）‖2＝1；

（3）令

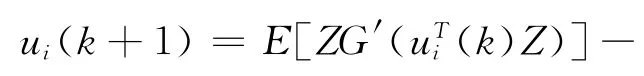
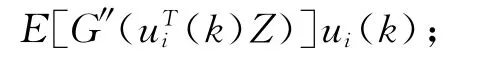
（5）如不收敛，回到步骤（3）。

采用本算法的优点是：由于采用牛顿法，使得收敛较有保证，可以证明它具有三阶的收敛速度[10]；迭代过程中不需要引入调节步长等人为设置的参数，因而更简单方便。

2 仿真

为了验证本文算法的有效性，这里令si（t）为源信号中的一路单位信号，yj（t）为对应的单位分离信号，残差r（t）＝si（t）－yj（t），分离结果的优劣用如下的误差函数来评估：

单位最大绝对误差：

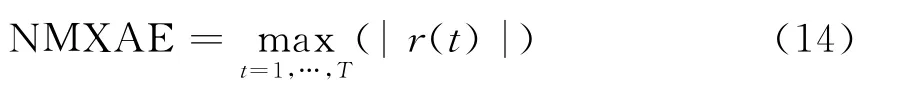
单位平均绝对误差：

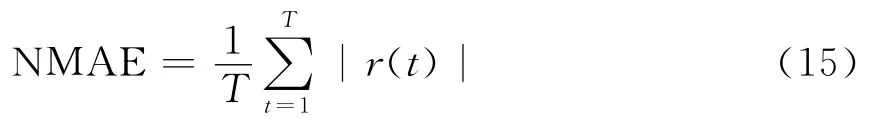
单位均方误差：

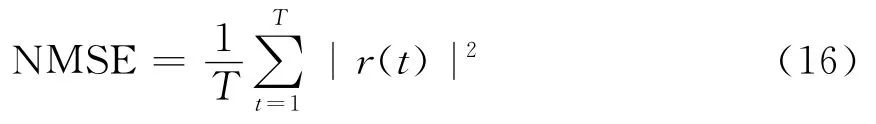
误差越小，说明算法越有效。

2.1 谐波源信号仿真

对于交流电弧炉系统，由于其在炼钢过程中的一些固有特点：电弧延迟发弧、电弧电阻的非线性、电弧游动、冶炼过程中电极同炉料的接触性短路、炉料的崩塌、炉料成分的气化、氧化期内被熔金属的剧烈沸腾等原因，使得电弧炉的电弧电压和电弧电流的变化很不规则，在此简化处理并由文献[12]得到交流电弧炉的电压变化曲线如图2中U21所示；由文献[13]得到饱和变压器的电压变化曲线如图2中U22所示，纵坐标为电压信号，横坐标为时间。

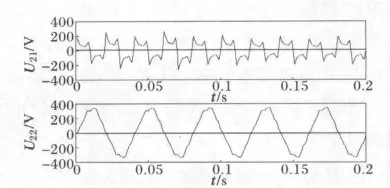
图2 交流电弧炉和饱和变压器的电压信号Fig.2 Voltage signals of AC－EAF and saturation transformer

为了模拟测量的电压信号，在此用一个随机产生的2×2矩阵对上述两个电压信号进行线性叠加，得到测量的电压信号如图3U31、U32所示。

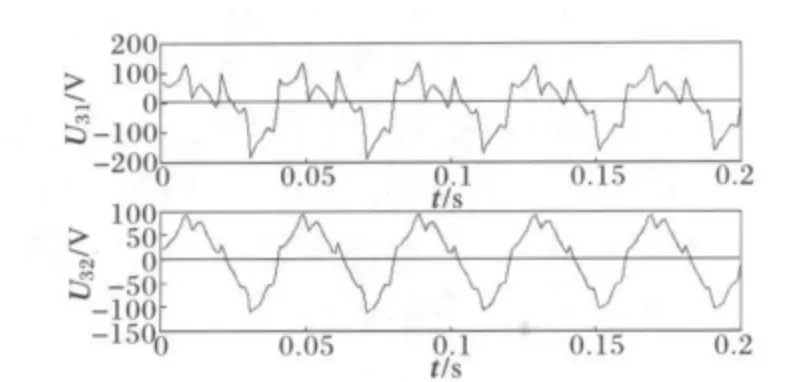
图3 测量的电压信号（Ⅰ）Fig.3 Measured signals of voltage（Ⅰ）

由图3可知测量的电压信号已完全失去谐波源信号的电压特性，用ICA 的方法可以分离出谐波源信号，仿真参数G 采用式（6）的表达式，应用本文算法得到分离后的电压信号如图4U41、U42所示。

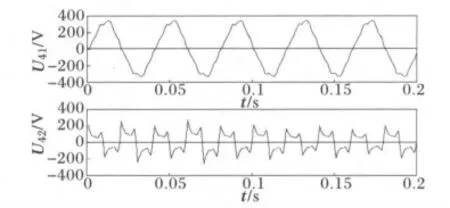
图4 分离的电压信号（Ⅰ）Fig.4 Separated signals of voltage（Ⅰ）

由于在ICA 算法中，分离后的电压信号与谐波源信号没有固定的对应关系[7]，所以要确定分离后得到的电压信号所对应的谐波源信号。为此构造一个相关系数矩阵[14]：

式中相关系数

由于越相似的电压信号其相关系数越大，故由c1j可确定分离后的电压信号中与第一个谐波源信号相对应的电压信号，c2j可确定分离后的电压信号中与第二个谐波源信号相对应的电压信号，以此类推可将谐波源信号中各电压信号辨别出来。应用式（17）对上面分离后得到的电压信号进行计算得到相关系数矩阵为

由此可知分离后的电压信号U41对应的是饱和变压器的电压信号U22，U42对应的是交流电弧炉的电压信号U21，由式（14）～（16）计算得到分离信号与源信号的误差如表1所示。

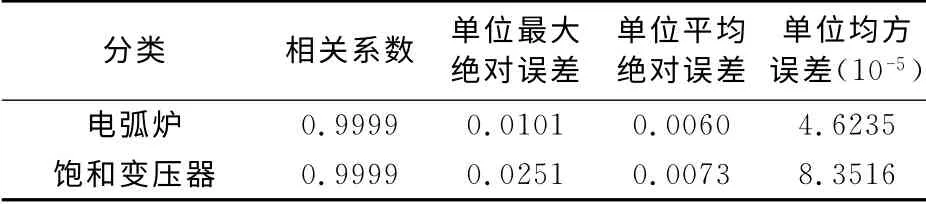
表1 分离后电压信号与谐波源信号的误差Tab.1 Errors between the separated voltage signal and signal of harmonic source

由表1可知，该算法的单位最大绝对误差依次为0.0101、0.0251，单位均方误差更小，数量级为10－5，各相关系数接近1，说明该算法能够很好地完成谐波源的辨识。

2.2 带有噪声的谐波源信号仿真

为了说明该算法在更复杂情况下的有效性，在2.1中两个谐波源的基础上再加上一个模拟谐波源的电压信号，其表达式为

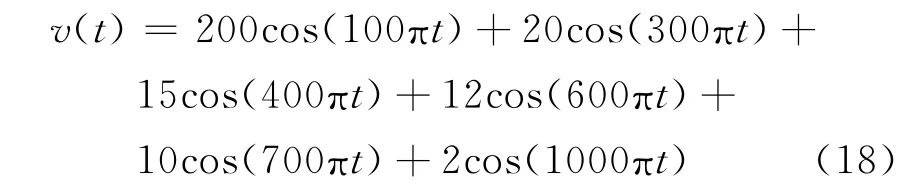
另外为了检验该算法的抗噪性能，用一零均值的随机信号来模拟系统中的噪声，在此也将其看作一个谐波源信号，如图5所示，U51～U54依次为交流电弧炉的电压信号，饱和变压器的电压信号，及噪声。用4×4的随机矩阵对谐波源信号进行线性叠加，得到测量的电压信号如图6U61～U64所示。

再用本文算法对测量的电压信号进行计算，得到分离后的电压信号如图7所示。

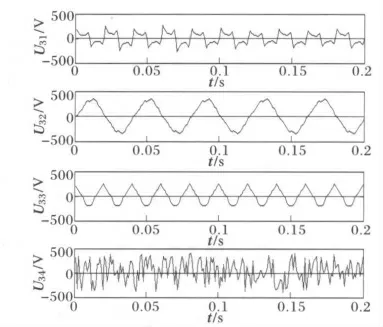
图5 谐波源电压信号（Ⅱ）Fig.5 Voltage signals of harmonic sources（Ⅱ）

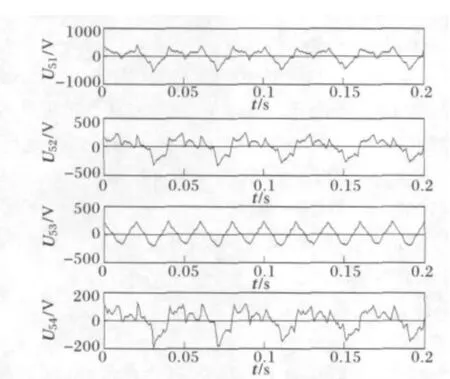
图6 测量的电压信号（Ⅱ）Fig.6 Measured signals of voltage（Ⅱ）

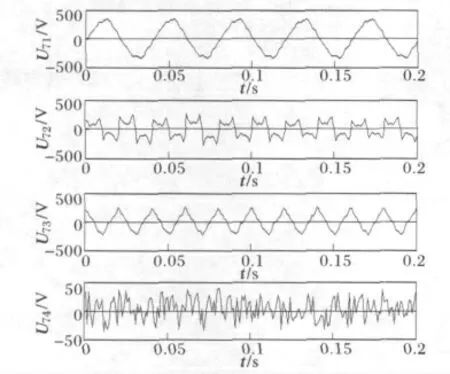
图7 分离的电压信号（Ⅱ）Fig.7 Separated signals of voltage（Ⅱ）

应用式（17）对分离后的电压信号进行计算得到相关系数矩阵为

由相关系数矩阵可知分离后的电压信号中U71与饱和变压器的电压信号对应，U72与交流电弧炉的电压信号对应，U73与模拟谐波源的电压信号对应，U74与噪声信号对应。由式（14）～（16）计算得到分离信号与源信号的误差如表2所示。

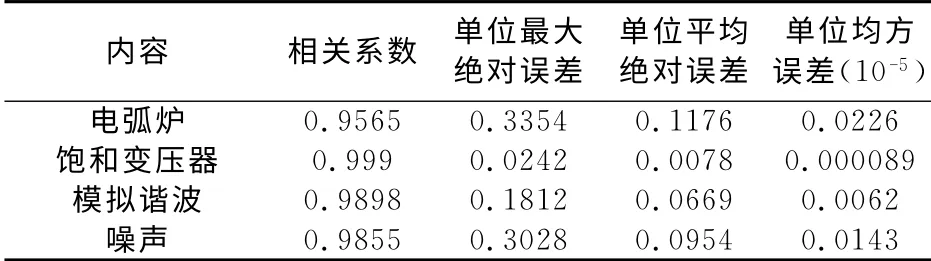
表2 有噪声时分离后电压信号与谐波源信号的误差Tab.2 Errors between the separated voltage signal and signal of harmonic source with a noise

由表2可知，相对于2.1的仿真结果，有噪声时分离后的电压信号与谐波源信号的误差增大，相关系数减小。但单位均方误差仍能保持10－2的数量级，各相关系数也在0.95以上，误差仍在可以接受的范围内。说明本文算法具有很好的鲁棒性。

3 结语

本文将谐波源辨识问题抽象为盲源分离问题，并运用该领域流行的独立分量分析法进行分析，通过仿真研究表明ICA 方法能够分离多种不同类型的谐波源信号，可以准确地对谐波源进行辨识；即使是在有噪声的条件下也能取得较好的抗噪效果，说明该方法具有很强的鲁棒性。本文算法在电力系统应用处于初级阶段，在对具有复杂谐波源的网络，还需要做更进一步的研究。

[1]张哲，陈红坤（Zhang Zhe，Chen Hongkun）.谐波源辨识研究的现状和发展（Status and development of harmonic source identification）[J].电力系统及其自动化学报（Proceedings of the CSU－EPSA），2005，17（5）：37－41.

[2]肖湘宁.电能质量分析与控制[M].北京：中国电力出版社，2004.

[3]毕会静（Bi Huijing）.供电系统谐波辨识的研究（The Study of Harmonic Identification of Power Supply System）[D].保定：华北电力大学电气与电子工程学院（Baoding：College of Electrical and Electronic Engineering of North China Electric Power University），2006.

[4]范沙浪（Fan Shalang）.基于神经网络的谐波测量方法研究（Research of Harmonic Measurement Method Based on Neural Network）[D].西安：西安理工大学自动化与信息工程学院（Xi＇an：College of Automation and Information Engineering of Xi＇an University of Technology），2005.

[5]吴强，王行愚（Wu Qiang，Wang Xingyu）.基于独立分量分析的图像融合算法（Image fusion algorithm based on independent component analysis）[J].计算机工程（Computer Engineering），2007，33（10）：220－221，224.

[6]刘洋，邱天爽，毕晓辉（Liu Yang，Qiu Tianshuang，Bi Xiaohui）.基于独立分量分析和遗传算法的诱发电位提取新方法（An ICA and genetic algorithm based EP extraction method）[J].中国生物医学工程学报（Chinese Journal of Biomedical Engineering），2007，26（3）：349－354.

[7]王毅，牛奕龙，陈海洋（Wang Yi，Niu Yilong，Chen Haiyang）.独立分量分析的基本问题与研究进展（Independent component analysis：problems and progresses）[J].计算机工程与应用（Computer Engineering and Applications），2005，41（27）：38－42，82.

[8]杨福生，洪波.独立分量分析的原理与应用[M].北京：清华大学出版社，2006.

[9]Hyvarinen Aapo.Survey on independent component analysis[J].Neural Computing Surveys，1999，2（4）：94－128.

[10]Hyvarinen A，Karhunen J，Oja E.Independent Component Analysis[M].Hoboken：John Wiley ＆Sons，2001.

[11]Hyvärinen Aapo.Fast and robust fixed－point algorithm for independent component analysis[J].IEEE Trans on Neural Networks，1999，10（3）：626－634.

[12]王丰华（Wang Fenghua）.电弧炉建模研究及其应用（Study of Modeling the Electric Arc Furnace and Its Application）[D].上海：上海交通大学电子信息与电气工程学院（Shanghai：School of Electronic Information and Electrical Engineering of Shanghai Jiaotong University），2006.

[13]刘卫东，兰之达，刘中岳，等（Liu Weidong，Lan Zhida，Liu Zhongyue，et al）.电力变压器的非线性模型（Nonlinear models for power transformers）[J].东南 大 学 学 报（Journal of Southeast University），1993，23（2）：82－89.

[14]王毅，牛奕龙，陈海洋.盲信号处理[M].北京：国防工业出版社，2006.