基于能量守恒定律的电弧炉动态模型

吕相宇，王存旭，王 宁，张超臣，段莹莹，高浩然

（1.沈阳工程学院a.研究生部；b.自动化学院，辽宁 沈阳 110136；2.国网沈阳供电公司，辽宁 沈阳 110000；3.国网辽宁省电力有限公司 检修分公司，辽宁 沈阳 110000）

现有电弧炉模型在电弧炉进行冶炼过程中并不能很好地体现其动态阻抗特性[1]。因此，本文通过在电弧炉电弧中加入不同信号来体现电弧炉动态特性，建立符合其时变性的动态模型。

1 基于能量守恒定律的交流电弧炉模型

由于电弧炉电弧在冶炼过程中所呈现的多变性与随机性，所以在研究电弧炉模型时需要建立电弧的数学模型。

1.1 电弧炉电气系统的状态方程

由电弧炉构成的系统可看成一个含源的线性网络，利用戴维南等效电源定理化简此类网络后其结果不会受负载特性影响[2]。因此，在忽略变压器耦合时对励磁回路产生的干扰以及设定电弧炉负载三相稳定前提下，此时的电路可以等效为变压器二次侧。在忽略无功补偿电容的情况下，其折算后的等效电路如图1所示。

图1 三相电弧炉的等效电路

图1 中，电炉变二次侧的电阻和电感为R1、L1；电弧炉电气系统构成部分短网中的单相等效电阻、电感为R2、L2；其内部互感为M。令R=R1+R2，L=L1+L2，则电路可以进一步简化，如图2所示。

图2 三相电弧炉的简化等效电路

根据基尔霍夫电流定律可列出电路方程如下：

进一步化简可得到如下状态方程：

式（2）为最后化简所得的电弧炉电气状态方程。

假设交流电弧炉三相平衡，则可得其单相等效电路，如图3所示。

图3 电弧炉三相平衡时的等效电路

由基尔霍夫定理可列出电路方程如下：

通过化简变换后可得到电弧炉电气系统的状态方程为

若系统存在无功补偿电容时，则电弧炉电气部分的等效电路如图4所示。

图4 考虑无功补偿时的单相等效电路

根据基尔霍夫定理可列出无功补偿电容存在时的电气方程如下：

在假设电弧炉系统三相平衡且存在无功补偿电容时，通过消去i，对原式进行化简可得到其电气系统的微分方程为

由上面各式可知，在写出电弧半径表达式的前提下，电弧炉电路中的电压、电流可以通过电气方程求出。

1.2 电弧炉电弧数学模型的建立

随着交流电弧炉冶炼过程的变化，其内部电流变化的不确定性使得电弧处于不稳定状态，所表现的伏安特性也为动态特性[3]。图5 为电弧炉典型的动态阻抗特性。通过图5a 可看出电弧炉冶炼过程中其内部电压产生严重畸变，电弧电流波形虽然变化并不剧烈，但在零点时也出现了“零休”现象[4]。从图5b 中可见电弧炉伏安特性呈非线性状态，且周期内变化剧烈。

图5 电弧炉电流电压典型曲线

以能量守恒定律为依据，建立非线性微分方程，可以得到电弧功率的平衡方程[5]为

式中，p1为以热量形式散发出的功率；p2为改变电弧半径的功率；p3为电弧功率和转换为热能的总功率。

在只考虑电弧半径散热忽略其它影响电弧热能散失的前提下，可以得出：

因此，状态变量为电弧半径r，当电弧周围热量没有散失且炉内温度明显很高时，p1与电弧半径没有关系，这种情况下n=0；若不考虑周围温度变化对于电弧的影响时，此时电弧长度较长，取n=1；当电弧长度在冶炼过程中变短时，其产生的主要影响在电弧的横截面积上，这时取n=2。

在电弧周围温度变化时，其内部能量导数以及电弧半径的变化与p2成正比关系，此时可以得出：

这里假设弧柱的电阻率和rm成反比，则可以得出：

式中，m=0,1,2，随着电弧半径的增大，温度越高。

将赋值后的式（8）～式（10）代入式（7）后即可得到下列非线性微分方程：

式中，r(t)为电弧半径；i(t)为电弧电流；模型系数k1、k2、k3数值已知；n、m为模型参数。

电弧电压的表达式如下：

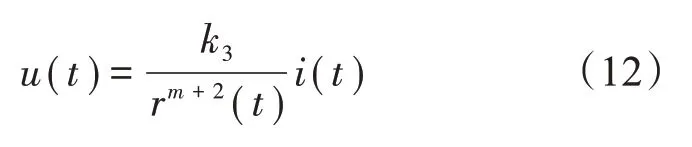
为了充分体现电弧炉的时变特点，在基于能量守恒定律建立的微分方程中设置其电弧半径以及瞬时电流为其输入量，此时电弧炉的电导为状态变量[5]。由于在不同冶炼过程中的温度变化，n、m的取值也随之变化，在内部温度过高的熔化期时，n=2，m=0，此时可体现出此类负荷的电压波闪等电能质量问题。

式（11）乘以rm+2(t)，可得：

其中，k=，根据文献[6]提供的参数辨识数据，此时参数k1=628.4，k2=0.53，k3=0.000 7，将所有参数带入到式（16）中，可得：

函数y(t)的最终表达式可通过式（17）得出，将y(t)表达式代入式（14）后即可得到电弧半径r(t)的表达式，再将所得表达式代入式（12）中即可得到电弧电压u(t)的表达式。

2 三相交流电弧炉动态模型调制

电弧电压波闪、谐波畸变产生的根本原因是在电弧炉冶炼过程中周期不同导致弧长的快速不规则变化[7]。为了使电弧炉输出电压u(t)具有周期性、随机性以及混沌性，通常将这些外部特点在基于调制原理的基础上加到电弧上。

为了使电弧半径所示信号出现周期变化特性，将正弦信号加入到电弧半径r(t)中，此时可得rs(t)为

电弧的随机性采用高斯随机分布进行调制：

式中，φg为考虑到高斯分布电弧所产生的非线性信号；β为调制系数。

为了体现电弧炉冶炼过程中电弧的混沌特性，采用文献[8]中现有的混沌模型并将混沌信号加入到电弧半径的仿真电路中，此时可得到：

式中，δ为调制系数；φh为低频混沌信号。

考虑到冶炼时电弧炉阻抗特性的时变性以及三相取值的不同，将调制系数区间设为0～2.0，此时所搭建的可体现三相不平衡这一特点的电弧炉模型框图如图6所示。

图6 电弧炉动态模型

3 电弧炉模型仿真分析

本文所搭建的电弧炉仿真模型参数来源于山东某制镍厂，将表现电弧炉特性的3 个信号加入调试好的r(t)之后，并将其放入前面所搭建的稳态模型后，此时利用Matlab搭建的电弧炉动态模型进行仿真，如图7所示。

图7 电弧炉仿真模型电路

所搭建电弧炉子系统模型如图8所示。

图8 电弧炉子系统模型电路

在仿真软件中运行所搭建电弧炉模型后所得出的电弧炉电压、电流波形如图9、图10所示。

图9 单相负载电压波形

图10 单相负载电流波形

从图9 中可以看出，波形呈近似方波波动，完全偏离正弦波且波形产生严重畸变。在图10 中可以看出，电流波形在经过零点处下降速率变缓且出现冶炼负荷常见的“零休”现象，此时的波形也产生了严重的畸变。仿真图9、图10 所展示的特点以及波形与电弧炉典型波形图一致，因此，可验证本文所搭建的电弧炉动态模型可替代电弧炉用于实际电能质量分析以及治理中。

4 结论

本文首先在列出电弧炉电气系统状态方程后推导出电弧炉电阻与冶炼过程中电压、电流的关系，然后将正弦信号、高斯随机信号和蔡氏混沌信号加入到根据不同冶炼时间所推导出的电弧表达式中并建立电弧炉动态模型。在3个特征信号调制到电弧后并将瞬时电流作为输入，此时可表达出电弧电压与电流的数学表达式进而建立电弧炉动态仿真模型。将仿真波形与电弧炉典型电压、电流波形图进行对比，验证了本文所建模型的有效性。这种基础工作对后续电弧炉所带来的电能质量治理具有重要意义。