相空间中非完整非保守力学系统的一个动力学逆问题

张毅

(苏州科技学院 土木工程学院，江苏 苏州215011)

0 引言

动力学逆问题是分析力学研究的一个重要方面。由于动力学逆问题有非常广泛的应用，并且动力学逆问题的最终解决尚有问题，因此动力学逆问题常常引起力学家、数学家和工程技术专家的关注［1］。近年来，关于约束力学系统的动力学逆问题的研究已经取得了一些重要进展［1－8］。Whittaker在其经典著作中曾提到Bertrand 得到的一个结果［9］:对于已知结构的完整力学系统，作用力是未知的(假设力仅依赖于坐标而不依赖于速度)，当已知一个积分时可以求出未知力来。这是有关动力系统积分的一个重要性质，同时又是一个重要的动力学逆问题。Whittaker 指出［9］:但是，这个积分不能随意选取，而必须满足某些条件。尽管如此，这种只用极少信息就可以研究动力学逆问题的方法仍是一个相当好的结果［1］。Галиуллин［10］引入Еругин 函数，将结果加以推广。文献［11－12］进一步将结果推广到非完整力学系统，文献［13－14］给出了变质量非完整系统和相对运动动力学系统相应的结果。但是所有这些结果都是在位形空间中并且假设力仅依赖于坐标而不依赖于速度的情况下给出的。试图将Bertrand 的这个定理推广到相空间，并且不仅考虑非保守力依赖于广义坐标情况，也考虑非保守力依赖于广义动量的情况。并给出了若干算例加以说明。

1 完整非保守系统的Bertrand 定理

假设力学系统的位形由n 个广义坐标qs，s =1，…，n，来确定，其所受约束是理想、完整的，系统的广义动量和Hamilton 函数为

式中L 为Lagrange 函数。在正则变量p，q 下，系统的运动微分方程可表示为

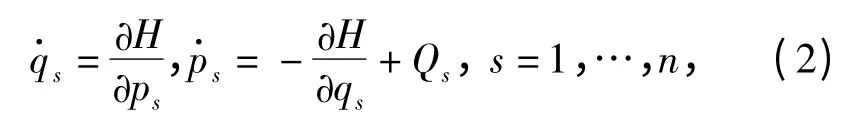
式中Qs=Qs(t，q，p)为非保守力。

假设已知非保守系统(2)式的一个积分

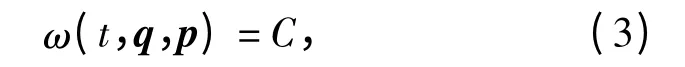
式中ω 对其所有变量有连续的偏导数。当C 为任意常数时，(3)式是系统的第一积分;当C 为某固定常数时，(3)式是系统的特殊积分。将(3)式对t 求导数，并引进Еругин 函数［10］，则有

式中Φ 称为Еругин 函数。当C 为任意常数时，有Φ=0;当C 为某固定常数时，Φ 为满足Φ|ω=C=0的任意函数。Еругин 函数的引入，对研究动力学逆问题，特别是建立稳定系统和构建规划运动系统具有重要意义［10］。

将(2)式代入(4)式，得到

式中(ω，H)为泊松括号，有

下面分两种情况讨论。

1)如果非保守力Qs不依赖于广义动量。由于关系式(5)式仅包含q，p 和t，它对出现于其中任意独立的量，应是一个恒等式。因此，它对任意一个广义动量pk的偏导数应等于0，于是得到

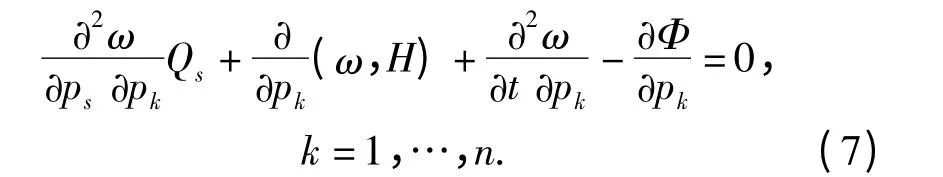
方程(7)式就是我们得到的为确定非保守力Qs的n个代数方程。解此代数方程组，便有可能确定非保守力Qs.如果给定的积分(3)式是系统的一个第一积分，即C 为任意常数时，则(7)式成为

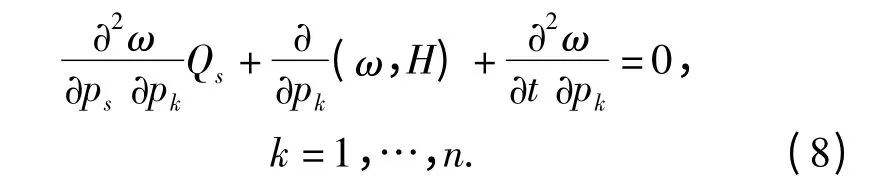
上述结果可归为如下命题1.

命题1 对于完整非保守力学系统(2)式，假设非保守力Qs不依赖于广义动量，那么，当已知积分(3)式为系统的第一积分时，非保守力Qs由代数方程(8)式确定;当已知积分(3)式为特殊积分时，非保守力Qs由代数方程(7)式确定。

2)如果非保守力Qs不依赖于广义坐标。将关系式(5)式对任意一个广义坐标qk求偏导数，得到

如果给定的积分(3)式是系统的一个第一积分，即C为任意常数时，则(9)式成为

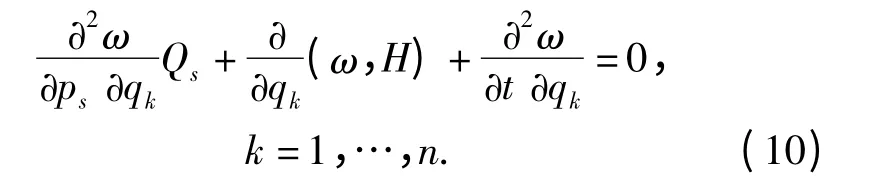
于是有

命题2 对于完整非保守力学系统(2)式，假设非保守力Qs不依赖于广义坐标，那么，当已知积分(3)式为系统的第一积分时，非保守力Qs由代数方程(10)式确定;当已知积分(3)式为特殊积分时，非保守力Qs由代数方程(9)式确定。

命题1 和命题2 构成了完整非保守系统中相空间中的Bertrand 定理。这是文献［9］中给出的位形空间的Bertrand 定理对相空间的推广，并且我们的结果包含了非保守力仅依赖于广义坐标和仅依赖于广义动量两种情况。

例1 研究Emden 问题［15］，其Lagrange 函数为

取广义动量和Hamilton 函数为

已知系统有一个第一积分［15］

假设系统的非保守力Q 不依赖于广义动量，则(8)式给出

解之，得

这是本问题的非保守力。

例2 仍研究Emden 问题，其Lagrange 函数［8］也可表为

通过整合分析发现：获得实习护生尊重和喜爱的带教老师必定德才兼备，不仅应具备扎实的专业知识、临床能力、教学能力，还应具备一定的教学热情和人文关怀能力。优秀的临床带教老师应能有计划、循序渐进的讲授临床实习要点；安排基础护理操作同时能抓住机会锻炼护生的专科操作技能，如骨脊柱外科轴线翻身、重症监护室(ICU)封闭式吸痰；在护生出差错时换位思考，以激励方式引导护生；多与护生沟通，关心爱护学生；注重培养护生交流能力，以身作则引导护生妥善处理护患关系。教学医院应根据教师准入标准筛选临床带教老师，通过时刻督导、定期培训、适时奖励带动临床带教老师的教学热情。

取广义动量和Hamilton 函数为

已知系统有一个第一积分［15］

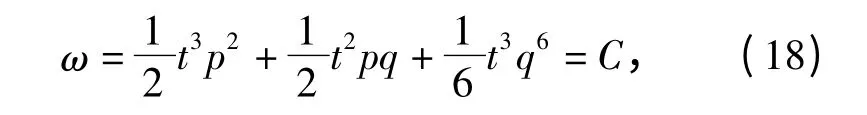
如果系统的非保守力Q 不依赖于广义坐标，则(10)式给出

解得

这是本问题的非保守力。

2 非完整非保守系统的Bertrand 定理

假设力学系统的位形由n 个广义坐标qs(s =1，…，n)来确定，系统的运动受有g 个理想Chetaev 型非线性非完整约束

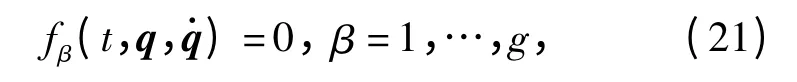
则非完整系统的运动微分方程为

式中:L 为Lagrange 函数;Qs为非保守力;λβ为约束乘子。设系统非奇异，则在运动微分方程(22)式积分以前，可由方程(21)式和(22)式求出约束乘子λβ作为t，q和非保守力Qs的函数，有［1］

将(23)式代入(22)式，便消除了乘子λβ，得到n 个二阶常微分方程，称为相应完整系统的运动微分方程。当初始条件满足非完整约束(21)式时，相应完整系统的解就给出原非完整系统的运动。

引入广义动量ps= ∂L/∂，在正则变量p，q 下约束方程(21)式可写成

相应完整系统的运动微分方程可表示为正则形式

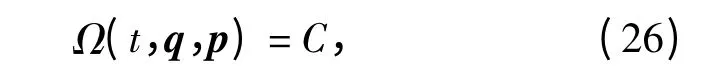
将(26)式对t 求导数，并引入Еругин 函数Φ，则有

当C 为任意常数时，有Φ =0;当C 为某固定常数时，Φ 为满足Φ|Ω=C=0 的任意函数。

将方程(25)式代入方程(27)式，有

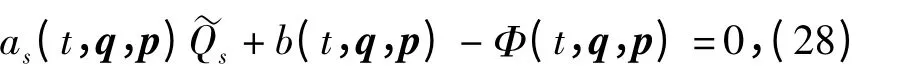
式中:

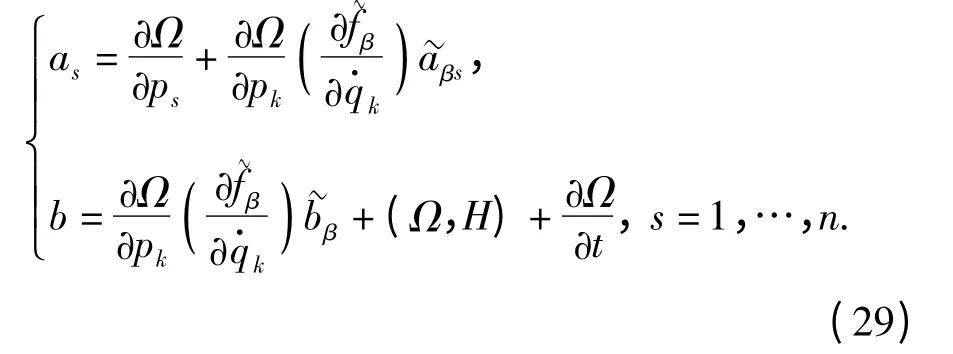
下面仍分两种情况研究。

方程(30)式就是我们得到的相空间中非完整非保守系统为确定其非保守力的n 个代数方程。解此代数方程组，便有可能确定非保守力如果给定的积分(26)式是系统的一个第一积分，即C 为任意常数时，则(30)式成为

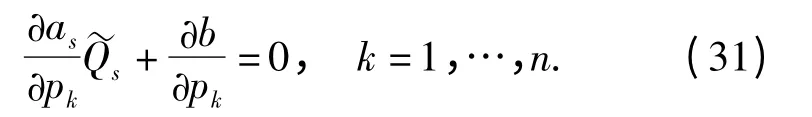
于是有

命题3 对于所论非线性非完整非保守力学系统，假设非保守力不依赖于广义动量，那么，当已知积分(26)式为系统的第一积分时，非保守力由代数方程(31)式确定;当已知积分(26)式为特殊积分时，非保守力由代数方程(30)式确定。

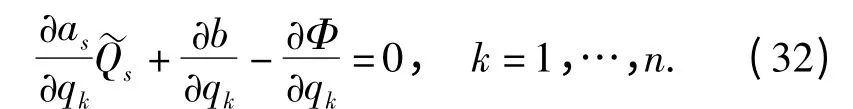
如果给定的积分(26)式是系统的一个第一积分，则(32)式成为

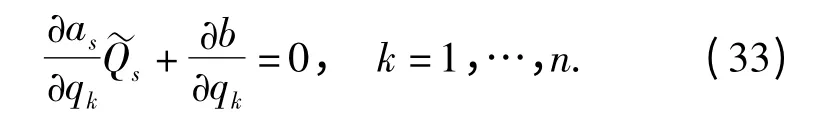
于是有

命题4 对于所论非线性非完整非保守力学系统，假设非保守力不依赖于广义坐标，那么，当已知积分(26)式为系统的第一积分时，非保守力由代数方程(33)式确定;当已知积分(26)式为特殊积分时，非保守力由代数方程(32)式确定。

命题3 和命题4 构成了非完整非保守系统中相空间中的Bertrand 定理。这是文献［1］中给出的位形空间的Bertrand 定理对相空间的推广，并且我们的结果包含了非保守力仅依赖于广义坐标和仅依赖于广义动量2 种情况。

例3 设非完整系统的位形由广义坐标q1、q2确定，系统的Lagrange 函数为

所受的非完整约束为

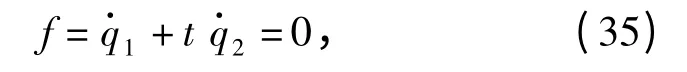
已知系统有一个第一积分

式中:k 为某固定常数;h 为任意常数。假设非保守力不依赖于广义动量，试求所受的非保守力和

方程(22)式给出

由方程(37)式和(35)式可解得

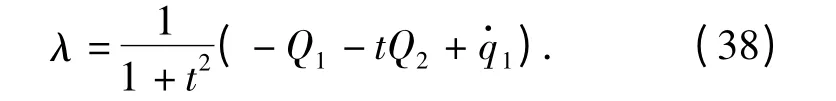
取广义动量和Hamilton 函数为

在正则坐标下，约束方程(35)式可写为

方程(25)式给出

(36)式可表示为

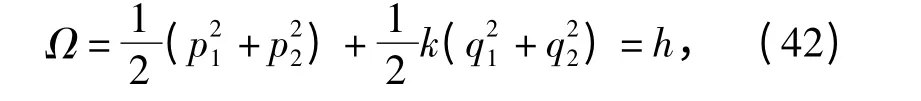
将(42)式对t 求导数，因h 是任意常数，故Еругин函数为0，因此有

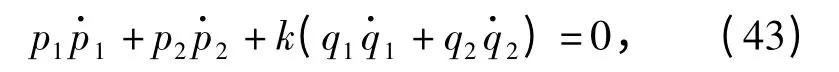
将方程(41)式代入(43)式，并利用约束(40)式，得到

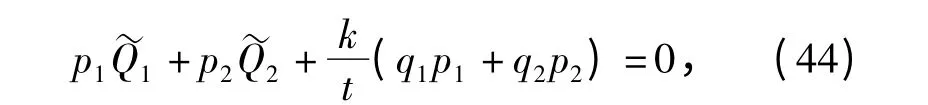
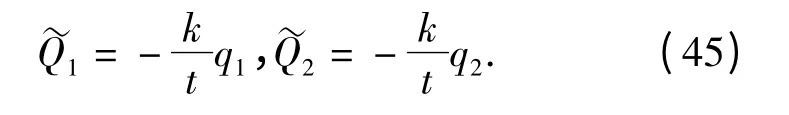
(45)式给出了本问题的非保守力。

3 结论

研究了非保守力学系统的一个逆问题，将Bertrand 定理推广到相空间中完整非保守力学系统和非线性非完整非保守力学系统。研究表明:已知相空间中完整非保守系统或非完整非保守系统的一个第一积分，就有可能确定作用在系统上的非保守力。主要结果为文中的4 个命题。

必须指出的是，由文中命题不一定能够唯一确定所有的非保守力。原因在于:1)当已知积分为特殊积分时，Еругин 函数除了满足条件Φ|ω=C=0 或Φ|Ω=C=0 外，仍是任意的;2)在非保守力的确定式中如果不是所有广义坐标或所有广义动量都出现的话，则方程数将小于n，或者确定式中某些非保守力的系数为0，在这些情况下，为最终确定非保守力，必须施加其他补充条件，例如关于稳定性或优化的限制等。

References)

［1］ 梅凤翔.动力学逆问题［M］.北京:国防工业出版社，2009.MEI Feng－xiang.Inverse problems of dynamics［M］.Beijing:National Defense Industry Press，2009.(in Chinese)

［2］ 丁光涛.Noether－Birkhoff 动力学逆问题［J］.中国科学:物理学、力学、天文学，2010，40(2):1514－1520.DING Guang－tao.Noether－Birkhoff inverse problem of dynamics［J］.Scientia Sinica Physica，Mechanica ＆ Astronomica，2010，40(12):1514－1520.(in Chinese)

［3］ 梅凤翔.非完整动力学逆问题的基本解法［J］.力学学报，1991，23(2):252－256.MEI Feng－xiang.Basic methods of solution for inverse problem of nonholonomic dynamics［J］.Acta Mechanica Sinica，1991，23(2):252－256.(in Chinese)

［4］ Bahar L Y.A unified approach to non－holonomic dynamics［J］.International Journal of Non－Linear Mechanics，2000，35(4):613－625.

［5］ 梁立孚，张耀良.广义拉格朗日逆问题研究［J］.哈尔滨工程大学学报，2000，21(2):64－68.LIANG Li－fu，ZHANG Yao－liang.On generalized Lagrangian inverse problems［J］.Journal of Harbin Engineering University，2000，21(2):64－68.(in Chinese)

［6］ LIU Feng－li，MEI Feng－xiang.Formulation and solution for inverse problem of nonholonomic dynamics［J］.Applied Mathematics and Mechanics，1993，14(4):327－332.

［7］ 张永发，梅凤翔.Birkhoff 系统动力学逆问题的两种提法和解法［J］.北京理工大学学报，1996，16(4):352－356.ZHANG Yong－fa，MEI Feng－xiang.Two ways of formulation and solutions of the inverse problem of the dynamics of Birkhoffian systems［J］.Transaction of Beijing Institute of Technology，1996，16(4):352－356.(in Chinese)

［8］ LI Guang－cheng，MEI Feng－xiang.An inverse problem in analytical dynamics［J］.Chinese Physics，2006，15(8):1669－1671.

［9］ Whittaker E T.A treatise on the analytical dynamics of particles and rigid bodies［M］.4th ed.Cambridge:Cambridge University Press，1952.

［10］ Галиуллин А С.Методы решения обратых задач динамики［M］.Моская:Наука，1986.

［11］ 梅凤翔.非完整动力学研究［M］.北京:北京工业学院出版社，1987.MEI Feng－xiang.Research on nonholonomic dynamics［M］.Beijing:Beijing Institute of Technology Press，1987.(in Chinese)

［12］ SHI Rong－chang，MEI Feng－xiang.On a generalization of Bertrand’s theorem［J］.Applied Mathematics and Mechanics，1993，14(6):537－544.

［13］ 张毅.变质量二阶线性非完整系统的广义Bertrand 定理［J］.苏州城建环保学院学报，1996，9(3):13－19.ZHANG Yi.A generalized Bertrand’s theorem for variable mass systems with linear second order nonholonomic constraints［J］.Journal of Suzhou Institute of Urban Construction and Environmental Protection，1996，9(3):13－19.(in Chinese)

［14］ 张毅.变质量非完整力学系统相对于非惯性系的广义Bertrand 定理［J］.北京理工大学学报，1996，16(增刊1):126－132.ZHANG Yi.A generalized Bertrand’s theorem for variable mass nonholonomic mechanical system relative to noninertial reference frame［J］.Transaction of Beijing Institute of Technology，1996，16(S1):126－132.(in Chinese)

［15］ 梅凤翔.李群和李代数对约束力学系统的应用［M］.北京:科学出版社，1999.MEI Feng－xiang.Applications of Lie groups and Lie algebras to constrained mechanical systems［M］.Beijing:Science Press，1999.(in Chinese)