三维运动声阵列对双点声源角跟踪指向性能研究

刘亚雷，顾晓辉

(南京理工大学智能弹药技术国防重点学科重点实验室，江苏 南京210094)

0 引言

运动声阵列角跟踪系统一般是由声传感器、阵列载体、末端制导控制等部分组成，通过运载工具将声阵列投放到探测目标的区域内，其一般可与飞行器、弹体或智能子弹药组成声探测系统。运动声阵列角跟踪技术也就是利用声目标在运动过程中本身的声波辐射，通过目标机动检测器及滤波算法来估计运动目标方位信息，再利用这些随时间变化的方位信息序列来估计出目标运动参数(速度、方向、距离)的技术，因此从跟踪本质上来说，运动声阵列跟踪技术是纯方位目标跟踪技术的一种［1］。运动声阵列在许多领域尤其是在军事领域中具有广泛的应用［2－4］，如美国陆军生产的一种灵巧弹药——智能子弹药就是应用运动声阵列实现对二维声目标进行定向跟踪，以及其在智能雷上的应用等。

未来战场是多种声源并存，除目标信号以外的所有声信号都为干扰信号，特别是有些干扰源的干扰信号与目标信号产生机理相同，声特性也十分相似，如:T59 主战坦克车速度在30～40 km/h 时声信号的功率谱主要能量集中在1 000 Hz 以下，为中低频率连续谱;一般汽车在速度为35 km/h 时基频一般在50～100 Hz 以内，汽车噪声信号与坦克和装甲车声信号有较多相似之处，特别是大型卡车;7.62 mm机枪的噪声信号为宽带信号，在带宽内能量分布均匀，半自动步枪在1 000 Hz 内能量比其他频带范围内的要高，且它的峰值频率一般在250～1 000 Hz范围内;火炮的噪声也为一宽带信号，信号在1 000 Hz内能量值较高，噪声峰值频率一般在80～500 Hz 范围内［5］。国内外对于声干扰的研究主要集中在水声干扰［6－8］，对于三维运动声阵列在多声源干扰下的角度跟踪指向问题目前还未见这方面的公开资料。国内外对于声阵列角跟踪问题主要是在声阵列相对地面静止的情况下进行了研究［9－11］，对于运动声阵列的角跟踪问题，文献［12－13］做了有关研究，但也仅研究了在单点声源下的角跟踪指向问题。

本文以多点声源干扰的基本原理为基础，分别从两个方面研究了三维运动声阵列在双点声源复合作用下的角跟踪指向性能。一方面通过建立运动声阵列在双点声源下的角度跟踪指向性能数学模型，分析了运动声阵列在点声源干扰时的角度跟踪性能，另一方面建立了评价等功率双点声源辐射的角度跟踪评价指标。

1 多点声源干扰原理

如图1所示三维运动声阵列在多源干扰下对真实目标的方位估计示意图。

以真实目标为坐标原点，建立系统坐标系，假设目标平面内共有n 个目标(伪目标)发出干扰声信号，如图中的A1，A2，A3，…，An，ri，i =1，2，3，…，n 为阵列与伪目标之间的距离，r，β，α 分别为阵列与真实目标之间的距离，俯仰角及方位角。则单个声辐射源的辐射声压［14］为

图1 多源干扰下运动声阵列对真实目标的方位估计示意图Fig.1 True target position estimated by dynamic acoustic array under the interference of multi－source

式中:p0为静态压强;ω =2πf 为角频率;k =2πf/c0为波数，c0为声速，取340 m/s.根据空间某点的声场是各个辐射声源形成的声场在该点的线性叠加，则平面上所有声目标发出的信号在三维运动声阵列处的合成场可以表示为:

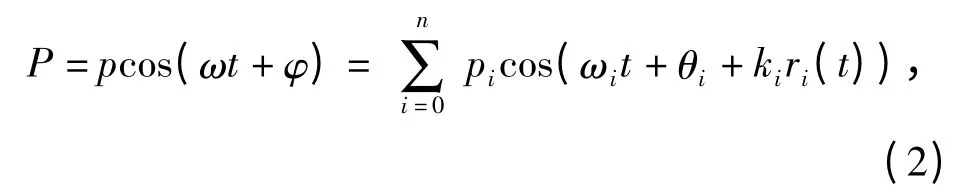
式中:i=0 对应的是真实目标，i =1，…，n 对应的是第i 个伪目标;pi、ωi、ki分布表示第i 个目标辐射源的声压幅度、辐射声信号的角频率、波数;θi表示第i个干扰目标辐射声源与二维真实目标之间的初始相位差;由于阵列与各个辐射声源之间存在相对运动，因此ri(t)是一个随时间变化的参数。令φi= θi+kiri(t)，根据(1)式、(2)式及矢量分解原理可得:

根据(2)式～(4)式可知，阵列接受的声信号为多个声源信号的叠加，由于战场目标的多样性，从而导致各个声源的频率也不相同，(2)式为远场合成声信号模型，其梯度方向不指向任何一个实际的辐射声源，因此对接受信号的方位估计并不是真实跟踪目标的方位信息，而是一个“空白”目标方位信息，如图1中的B 区域。

2 角度跟踪指向性能数学模型

根据上述分析，假设阵列接受的声信号由两个不同声源发出信号的合成，即假定目标区域内只存在一个伪目标及一个真实目标。如图2所示，为运动声阵列在双点声源下角度跟踪指向示意图。以二维真实目标为原点建立坐标系，x 轴指向北，z 轴垂直于地面指向上，y 轴按右手法则确定。在t 时刻运动声阵列的位置坐标为(x，y，z)，伪目标的位置坐标为(x1，y1)，真实目标与伪目标之间的距离为doA，声阵列接受合成声信号的方位与真实目标声辐射的方位之间的偏角为ΔθoB，双点声源对声阵列的张角为ΔθoA.

图2 双点声源下运动声阵列角度跟踪指向示意图Fig.2 Angle tracking pointing of dynamic acoustic array under the interference of dual acoustic source

为了分析方便，对数学模型可做如下假设:1)不考虑声信号的多径传播及非线性现象;2)不考虑由于各个声源的路程差而引起的相位差，即r1≈r2，且r1≈r2≫d，d 为真实目标与伪目标之间的距离;3)声传感器特性相同，各向同性;4)声阵列处于信号源的远场中，即声源传来的声信号是平面波;5)各传感器的噪声互不相关，且与待测信号也不相关;6)干扰声信号及真实声信号是窄带的;7)同一个目标发出的声信号在空间一点上被传感器接受到的声信号是单一频率声信号，也就是假设传感器接受的是单频信号。根据上述假设及多源干扰理论可知，真实目标及伪目标辐射的声信号到达声阵列处的声压分别为p1、p2，则有:

其中:θ0为两声源辐射声信号的初始相位差。

根据(2)式，可得合成声压

其中:幅度及相位分别为:

由于干扰声信号的存在，使得声阵列对目标的角度跟踪指向存在误差，从而声阵列的跟踪角度不为真实目标的真实角度，一般而言是指向于“空白”目标，如图2中的B 所示，从空间的角度分析，声阵列角度跟踪指向应为过声阵列几何中心的等相位线的法线方向［15］，则根据空间曲面切平面与法线知识可知，法线方程为:

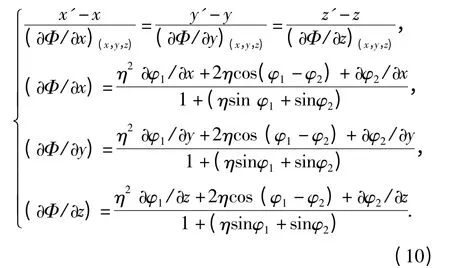
其中:η=p01/p02;(x，y，z)为声阵列在等相位线上的坐标值，也就为声阵列的位置坐标值。令z' =0，则可求得法线在xy 平面内的交点，也就是为图2中B的坐标值(x2，y2):

令:a=2ηcos(φ1－φ2)，b =η2ω1/c0，q =ω2/c0，则有:

根据假设可知r1≈r2，则(13)式～(14)式简化可得:

则声阵列偏离真实目标的距离

又令:κ = ω2/ω1，r1≫doA，r2≫doA，ζ =则有:ζ = 1，sin(ΔθoB)≈ΔθoB，sin (θoA/2)≈θoA/2，θoA/2－ΔθoB→0.因此，根据正弦定理有:

则运动声阵列偏离真实目标的角度

因此(17)式、(20)式组成了运动声阵列在双点声源下的角度跟踪指向性能数学模型。从战场多源干扰因素的角度来考虑，在t 时刻影响运动声阵列对真实目标角度跟踪指向性能的主要因素有:干扰声信号与真实目标辐射的声信号的频率值比、声压幅值比及两声源的相位差。

3 运动声阵列角度跟踪指向抗干扰性能分析

讨论1 伪目标与真实目标的声信号在频率上一致，声压幅值保持线性关系，即κ=1，此时(20)式可转化为:

1)当φ1－φ2=0，即伪目标与真实目标同相时，(21)式可转化为:

由η=p01/p02，当p01=0 时，η =0，即角跟踪区域内只存在伪目标，此时ΔθoB=θoA，声阵列角跟踪指向伪目标;当p02=0 时，η→∞，即角跟踪区域内只存在真实目标，此时ΔθoB=0，声阵列角跟踪指向真实目标。当0 ＜η ＜∞时，声阵列角跟踪方向指向伪目标与二维声目标连线之间。

2)当φ1－φ2=180°，即伪目标与真实目标反相时，(21)式可转化为:

分析(23)式可知，η=0，ΔθoB=θoA，声阵列角跟踪指向伪目标;η→∞，ΔθoB=0，声阵列角跟踪指向真实目标。与同相干扰不同的是，在η ＞1.5 之后，ΔθoB与θoA的关系出现负数系数关系，这主要是由于模型中的数学假设与实际情况的差别而导致，但是此负数系数的非常小，随着η 的增加，ΔθoB/θoA将趋于0.

如图3所示同相与反相时ΔθoB/θoA与η 的关系。可知，随着η 的增加，ΔθoB/θoA下降迅速，说明在运动声阵列在对两类同频率的声源目标进行角跟踪时，其角度跟踪指向于声强度高的目标。如图4所示不同η 值下的ΔθoB/θoA随(φ1－φ2)变化曲线，可知，在η ＜1 中，随着(φ1－φ2)的增加，ΔθoB/θoA的比值缓慢增加，这主要是声阵列受到伪目标的“双重干扰”，即为声强度干扰及相位干扰同时存在，从而导致声阵列角度跟踪指向于伪目标的概率增加;在η=1 时，ΔθoB/θoA的比值不随(φ1－φ2)变化，始终保持在0.5 上，这是主要是由于声阵列以声信号为探测手段，接受到的声强度对声阵列角度跟踪指向的影响程度大于相位干扰的影响程度，因此当两类声信号的声强相等时，声阵列角度跟踪指向于两目标连线的中点;在η ＞1 时，随着(φ1－φ2)增加，ΔθoB/θoA的比值缓慢的降低，这也说明了声信号的声强度干扰对声阵列角度跟踪指向的影响程度大于其相位干扰的影响程度。因此在同频率的双声源跟踪中，声强是影响声阵列角度跟踪指向的主要因素。

图3 同频率时同相与反相时ΔθoB/θoA与η 的关系Fig.3 Relationships of in－phase and opposed－phase ΔθoB/θoA at same frequency

图4 同频率不同η 值下的ΔθoB/θoA随(φ1－φ2)变化曲线Fig.4 Relationships between ΔθoB/θoA and (φ1－φ2)for different η at same frequency

讨论2 伪目标与真实目标的声信号的声压幅值一致，在频率上保持线性关系，即η=1，此时(20)式可转化为:

1)当φ1－φ2=0，即伪目标与真实目标同相时，(24)式可转化为:

由κ=ω2/ω1，当ω2=0 时，κ=0，即角跟踪区域内只存在真实目标，此时ΔθoB=0，声阵列角跟踪方向指向真实目标;当ω1=0 时，κ→∞，即角跟踪区域内只存在伪目标，此时ΔθoB=θoA，声阵列角跟踪方向指向伪目标。当0 ＜κ ＜∞时，声阵列角跟踪方向指向伪目标与二维声目标连线之间。

2)当φ1－φ2=180°，即伪目标与真实目标反相时，此时(24)式转化为:

(26)式同(25)式，因此分析结果也相同。

如图5所示同声强时同相与反相时ΔθoB/θoA与κ 的关系。可知，随着κ 的增加，ΔθoB/θoA也增加，但是增幅逐渐平缓，说明声阵列在对两类同声强度不同频率的声源目标进行角跟踪时，其角度跟踪指向于角频率高的目标，但是无论κ 多大，ΔθoB的角度不会超过θoA，说明了声阵列角度跟踪指向于两声源目标连线之间。如图6所示不同κ 下ΔθoB/θoA与(φ1－φ2)的关系曲线。由图可知，在κ 一定时，ΔθoB/θoA不随(φ1－φ2)的变化而变化，这主要是因为:

又根据假设r1≈r2，可知:

由(29)式可知，双点声源相位角的变化被包含在了频率值比的变化之内，同时也说明了两声源目标相位角的变化与频率值比的变化是相互关联的，不是两个独立的影响因素。

图5 同声强时同相与反相时，ΔθoB/θoA与κ 的关系Fig.5 Relationship of in－phase and opposed－phase ΔθoB/θoA at same frequency sound intensity

讨论3 伪目标与真实目标声信号的声压幅值、频率均保持线性关系，此时分析(20)式可转化为:

图6 同声强不同κ 值ΔθoB/θoA与(φ1－φ2)的关系曲线Fig.6 Relationships between ΔθoB/θoA and (φ1－φ2)for different κ in same sound intensity

1)当φ1－φ2=0，即伪目标与真实目标同相时:

2)当φ1－φ2=180°，即伪目标与真实目标反相时:

如图7～图8所示φ1－φ2=0 及φ1－φ2=180°时，ΔθoB/θoA随κ、η 的变化关系。可知，η 变化时，ΔθoB/θoA的变化程度较大，而κ 变化时对ΔθoB/θoA的影响程度较小，从而说明了η 是影响声阵列角跟踪指向的主要因素。

4 运动声阵列角跟踪抗点声源干扰评价指标模型

为了简化模型，如图9所示，可建立如下坐标系O'X'Y'Z':设声阵列飞行轨迹与双声源位于同一平面，双点声源之间距离2L，则以双点声源的几何中心O'建立直角坐标系，双点声源连线为X'，声阵列在O'X'Y'Z'坐标系下的弹道倾角为γ，根据上述分析可知，对于等功率双点声源辐射下，声阵列角度跟踪指向落点B 的坐标为(x2'，0，0)，其中x'2=L(r'1－r'2)/(r1' +r'2)，在O'X'Y'Z'坐标系下，根据正弦定理可知:

图7 φ1－φ2 =0 时，ΔθoB/θoA随κ、η 的变化关系Fig.7 Relationships between ΔθoB/θoA，κ，and η at φ1－φ2 =0

图8 φ1－φ2 =180°时，ΔθoB/θoA随κ、η 的变化关系Fig.8 Relationships between ΔθoB/θoA，κ，and η at φ1－φ2 =180°

其中:ξ=(r'1－r2)/(r1+r2);r3为此时角跟踪指向在O－X'Y'Z'坐标系下与X'Y'平面的交点到阵列的距离。

根据(33)式、(34)式可知:

图9 运动声阵列角跟踪抗双点声源干扰示意图Fig.9 Angle tracking of dynamic acoustic array under the interference of dual acoustic source

由于智能反坦克(BAT)子弹药的战斗部一般为聚能战斗部或是含能破片战斗部或是爆炸成型穿甲战斗部(EFP)，在对目标进行攻击时，战斗部的运动速度都在上千，甚至为几千，因此无论是坦克还是装甲车辆的运动速度此时都可以忽略。设弹药战斗部有效毁伤半径为rb，则弹药声阵列有效毁伤真实目标应满足:

将(37)式带入(38)式，可知:

(34)式有解的充分必要条件为:

令

(40)式为BAT 有效毁伤真实目标的充分必要条件，根据式中参数含义可知，(41)式为一无量纲实数，它是声阵列飞行速度、侧向过载，弹药有效毁伤半径，声阵列弹道倾角及双点源对声阵列张角的函数，因此可将(41)式函数定义为一个新的指标，即角度干扰指数(BODI)，并用于评价弹药声阵列在点声源干扰下有效打击真实目标的能力。角度干扰指数能够很好的描述声阵列对点声源目标的角度跟踪指向，其值越大，说明声阵列角度跟踪指向性能越低，同时也说明运动声阵列抗点声源干扰能力越低。

5 结论

1)本文建立了运动声阵列在双点声源复合作用下的角度跟踪指向性能数学模型，得到了影响运动声阵列角度跟踪指向性能的因素为:伪目标的干扰声信号与目标声信号的频率值比、声压幅值比及两声源的相位差。

2)从伪目标与真实目标的声信号在频率上一致，声压幅值保持线性关系、声压幅值一致，在频率上保持线性关系、声信号的声压幅值、频率均保持线性关系3 个方面，分析了频率值比、声压幅值比及两声源的相位差与运动声阵列角度跟踪指向性能之间的关系。即在同频率的双点声源跟踪中，声强是影响运动声阵列角度跟踪指向的主要因素，双点声源相位角的变化被包含在了频率值比的变化之内，同时也说明了两声源目标相位角的变化与频率值比的变化是相互关联的，不是两个独立的影响因素。

3)提出了包含运动声阵列的飞行速度、侧向过载，战斗部有效毁伤半径，运动声阵列的弹道倾角及双点声源对声阵列张角等参数的BODI 作为运动声阵列角度跟踪指向性能评价指标，为进一步研究运动声阵列对多声源目标跟踪理论奠定了基础。

References)

［1］ 刘亚雷，顾晓辉.改进的辅助粒子滤波当前统计模型跟踪算法［J］.系统工程与电子技术，2010，32(6):1206－1209.LIU Ya－lei，，GU Xiao－hui.Current statistical model tracking algorithm based on improved auxiliary particle filter［J］.Systems Engineering and Electronics，2010，32(6):1206－1209.(in Chinese)

［2］ Wu Y I，Wong K T，Lau S.The acoustic vector－sensor’s near－field array－manifold［J］.IEEE Transaction on Signal Processing，2010，58(7):121－125.

［3］ Zhang L，Wu X，Pan Q，et al.Multiresolution modeling and estimation of multisensory data［J］.IEEE Transaction on Signal Processing，2004，52(11):3170－3182.

［4］ 刘亚雷，顾晓辉.智能子弹对声目标CACEMD－VDAKF 跟踪算法研究［J］.仪器仪表学报，2011，32(4):748－755.LIU Ya－lei，，GU Xiao－hui.Tracking algorithm study of CEFMDVDAKF in brainpower submunition for sound－source bearing［J］.Chinese Journal of Scientific Instrument，2011，32(4):748－755.(in Chinese)

［5］ 周忠来.战场声目标抗干扰技术研究［D］.北京:北京理工大学，1999.ZHOU Zhong－lai.Research on anti－interference technique for acoustic target identification in the battlefield［D］.Beijing:Beijing Institute of Technology，1999.(in Chinese)

［6］ 周伟，惠俊英.基于声矢量自适应干扰抵消的逆波束形成［J］.兵工学报，2010，31(9):1188－1192.ZHOU Wei，HUI Jun－ying.Inverse beam forming based on coherent interference vector adaptive canceling［J］.Acta Armamentarii，2010，31(9):1188－1192.(in Chinese)

［7］ 周明，初磊.高频噪声干扰器干扰主动声自导鱼雷仿真研究［J］.兵工学报，2010，31(3):327－330.ZHOU Ming，CHU Lei.Simulation on active acoustic homing torpedo jammed by the high－frequent noise jammer［J］.Acta Armamentarii，2010，31(3):327－330.(in Chinese)

［8］ Braga B F.History of United States torpedo defense from worldwarⅡto present［C］∥UDT Europe 2000 Conference.LaSpezia:UDT，2000:10－15.

［9］ Moran M L，Greenfield R J，Wilson D K.Acoustic array tracking performance under moderately complex environmental conditions［J］.Applied Acoustics，2007，68(10):1241－1262.

［10］ 孙书学，吕艳新，顾晓辉，等.双三角形声学靶信息融合定位模型［J］.兵工学报，2008，29(9):1094－1098.SUN Shu－xue，LU Yan－xin，GU Xiao－hui，et al.Based on information fusion shots location with acoustic target composed of dual triangle［J］.Acta Armamentarii，2008，29(9):1094－1098.(in Chinese)

［11］ 顾晓辉，王晓鸣.用双直角三角形阵对声目标定位的研究［J］.声学技术，2003，22(1):44－47.GU Xiao－hui，WANG Xiao－ming.Location of acoustic target with dual right－triangles array［J］.Technical Acoustics，2003，22(1):44－47.(in Chinese)

［12］ 孙书学，顾晓辉，吕艳新，等.弹载声阵列原理及定位算法［J］.弹道学报，2009，21(1):95－98.SUN Shu－xue，GU Xiao－hui，LU Yan－xin，et al.Principle and localization algorithm of missile－borne acoustic array［J］.Journal of Ballistics，2009，21(1):95－98.(in Chinese)

［13］ 孙书学，吕艳新，顾晓辉.BAT 子弹药对二维声目标的角跟踪［J］.火力与指挥控制，2008，33(12):113－116，120.SUN Shu－xue，LU Yan－xin，GU Xiao－hui.Bearing－only tracking of 2－D acoustic target with BAT［J］.Fire Control and Command Control，2008，33(12):113－116，120.(in Chinese)

［14］ 马大猷.现代声学理论基础［M］.北京:科学出版社，2010:26－31.MA Da－you.Modern acoustics theoretical basis［M］.Beijing:Science Press，2010:26－31.(in Chinese)

［15］ 艾名舜.反辐射导弹抗有源诱偏中信号处理技术研究［D］.西安:第二炮兵工程学院，2011.AI Ming－shun.Research on techniques signal processing in the anti－radiation missile antagonizing active decoy［D］.Xi’an:The Second Artillery Engineering College，2011.(in Chinese)