基于涡轮发电机输出频率的迫弹外弹道辨识方法研究

高敏，敬亚兴，刘秋生，吕静

(1.军械工程学院 导弹工程系，河北 石家庄050003;2.军械工程学院 弹药工程系，河北 石家庄050003)

0 引言

弹道辨识技术不仅是弹道修正的基础和关键技术，而且也可为创新性地开展引信安保机构设计和引信定高提供技术支撑，国内外现已进行广泛研究，提出如下弹道辨识方法:利用传感器测得初速和弹道上最小速度值辨识弹道［1］;基于质点弹道，利用速度传感器和定时器测得弹道最小速度点的速度值及其出现时间，作为弹道参数特征值反推等效初速和射角，进而确定弹丸实际飞行弹道［2］;利用动压式测速传感器测量弹丸在弹道上升段飞行过程中的速度，利用速度－时间序列反推等效初速和射角，进而确定弹丸实际飞行弹道［3］;基于弹丸初速和弹道初始段弹丸的纵轴向加速度辨识弹道［4］;利用GPS接收机获取弹道下降段位置和速度信息进行弹道辨识［5］;利用引信涡轮交流发电机输出频率与迫击炮弹速度之间的关系计算或查询装药号，利用引信涡轮交流发电机输出频率和射频发射接收机获取的多普勒频率计算射角，进而确定弹道［6］。上述弹道辨识方法理论可行，但工程应用或多或少还面临一些问题，如弹载传感器、射频发射接收机的实现及成本问题、最小弹速出现时间准确获取问题、弹道辨识计算量问题等。

涡轮发电机作为电源已在迫弹引信上得到广泛应用［7］，它利用弹道空气压力作为驱动力，推动其转子高速旋转进而产生电能，其输出的交变电信号的频率、幅值与转子转速有关，因此其输出信号能敏感弹丸速度变化。利用该特性，将涡轮发电机作为弹道峰检测器用于引信解除保险已获得成功应用［8］，但将其作为速度传感器进行深入应用研究的报道较少见。本文将引信涡轮发电机作为速度传感器进行弹道辨识，在默认弹丸弹道系数已知的前提下，提出了利用涡轮发电机输出频率信息辨识弹丸初速和射角的方法。

1 涡轮发电机输出频率分析

1.1 涡轮发电机输出频率特性

对于出炮口后作惯性飞行的弹药，文献［9－10］和射击试验测量数据表明，涡轮发电机输出频率曲线如图1所示。

图1是根据射击试验弹载频率测量设备测试数据所得出的，由于所用测量设备对100 Hz 以下的频率数据进行了归零处理，故图1中频率变化曲线上频率为0 的曲线段与实际存在差异。

图1 涡轮发电机输出频率曲线Fig.1 Output frequency curves of turbine alternator

当全弹道上进入涡轮发电机的气流速度(主要取决于弹速)大于等于涡轮发电机启动后维持其转动所需的最小风速时，涡轮发电机输出频率曲线为具有两个极值的曲线。出炮口后，涡轮发电机输出频率先迅速增大(由涡轮发电机启动迟滞造成)，然后随弹速的降低而降低，过了最小弹速之后，随弹速的增大而增大。

如果弹道上最小弹速附近，存在进入涡轮发电机的气流速度小于涡轮发电机启动后维持其转动所需的最小风速时，涡轮发电机将会停转。此种情况下，涡轮发电机输出频率变化规律如下:出炮口后，涡轮发电机输出频率先迅速增大，然后随弹速的降低而降低直至为0，之后，当弹丸速度增大到能使涡轮发电机重新启动的速度后，输出频率才随弹速的增大而增大。

1.2 可利用信息分析

涡轮发电机输出频率曲线的第1 个上升段是由涡轮发电机启动迟滞形成的，其上输出频率值并不真实地反映弹速变化，因此不利用该段频率－时间信息开展弹道辨识。但是该上升段结束点对应的最大频率值及其出现时刻能够定性反映初速和射角的大小。弹丸初速越大、射角越小，最大频率值越大、出现时刻越靠后，因此频率最大值及出现时刻可作为辨识结果的检验信息。

涡轮发电机输出频率曲线的下降段，输出频率跟随弹速变化，能够充分反映弹速信息，因此可利用这一段的频率－时间信息获取弹速－时间信息。当全弹道涡轮发电机不发生停转时，对应最小弹速，频率曲线下降段末存在非零最小输出频率。因为最小弹速点附近弹速变化缓慢，相应地，该点附近涡轮发电机输出频率低且变化也很缓慢，因此利用弹载高速频率测量设备的测试数据能够精确获取与最小弹速对应的非零最小输出频率值;加之频率转化为速度时是高倍缩小，故利用非零最小输出频率可以精确获取最小弹速。但是受弹载频率测量设备启动时间不一定在炮口、弹丸章动等影响，非零最小输出频率出现时刻可否作为最小弹速出现时刻有待深入研究。当弹道上涡轮发电机存在停转时，最小弹速附近涡轮发电机输出频率持续为0，此时不能获取最小弹速，但可根据涡轮发电机启动后维持其转动所需的最小风速和弹丸初速指标粗略判定涡轮发电机存在停转的射角范围。由于空气弹道弹速曲线非对称、弹丸存在章动等，能否利用频率曲线上频率值为0 的两个端点时间计算最小弹速时间有待深入研究。

涡轮发电机输出频率曲线的第2 个上升段，弹丸位于最小弹速点后的弹道降弧段，虽然输出频率反映弹速信息，但考虑到为弹道辨识计算以及后续应用留出时间，故弹道辨识时不利用该段信息。

根据上述分析，只利用涡轮发电机输出频率曲线下降段(含频率极小值点)信息开展弹道辨识。需要指出的是，涡轮发电机输出频率与进入涡轮发电机的气流速度直接相关，而进气流速度除主要取决于弹速外，还受风、弹丸章动等影响，对此，应从高速高精度测量涡轮发电机输出频率、准确获取涡轮发电机输出频率与进气流速度对应关系［8－11］、消除风和弹丸章动等不利影响3 个方面来保证根据涡轮发电机输出频率所求解的弹速的准确性。

2 弹道辨识总体方案

由于涡轮发电机作为电源已在迫击炮弹引信上得到应用;加之迫击炮弹初速低，通常采用大射角射击，当射角大到一定程度，涡轮发电机在弹道上可能停转，对其研究将使所得结论更具全面性，因此本文以在迫击炮弹引信上应用为背景开展研究。

由于应用对象初速小，且飞行稳定，故选用非标准气象条件下的质点弹道方程组作为弹道仿真方程组，以某型迫击炮弹性能参数和标准气象条件作为弹道仿真初始条件。非标准气象条件会导致弹道辨识结果存在偏差，实际应用时应加以修正。

利用弹道仿真平台，得到不同初速与射角时的弹速曲线，如图2所示。可看出:越靠近起点，同一初速下单纯由射角变化引起的弹速变化范围越小，且弹速大小主要取决于初速的大小;越远离起点、靠近最小弹速点，由射角变化引起的弹速变化范围越大;初速和射角对最小弹速出现时刻和大小均有影响。初速越高，由射角引起的最小弹速变化范围越大;射角越大，最小弹速主要取决于射角。

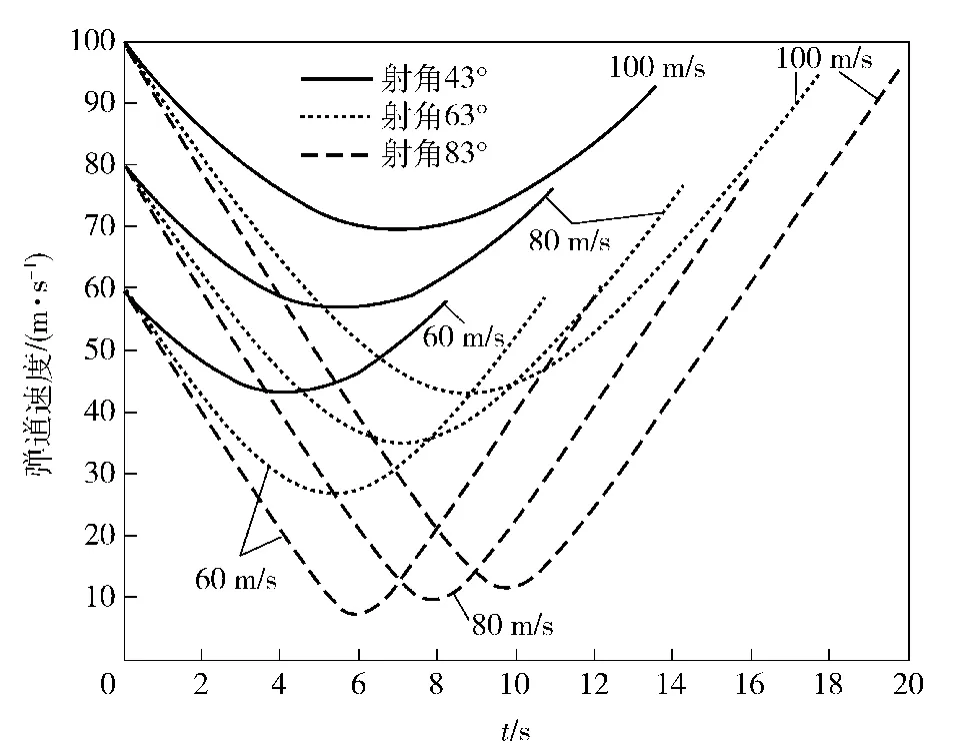
图2 不同初速与射角时的弹速曲线Fig.2 Projectile velocity curves under different muzzle velocities and angles of fire

上述结论表明:利用起点附近时刻的弹速值可以推算出初速(实际为一个小的速度区间);利用远离起点、靠近最小弹速点的弹速值或最小弹速值，结合推算出的初速，可以推算出射角。

结合对涡轮发电机输出频率可利用信息的分析，提出如下弹道辨识思路:根据涡轮发电机最小输出频率判断涡轮发电机是否停转;涡轮发电机全弹道不停转时，利用涡轮发电机输出频率曲线下降段靠近炮口某一时刻t1的输出频率和最小输出频率对应的弹速值推算初速和射角;涡轮发电机停转时，利用t1时刻的输出频率和涡轮发电机输出频率曲线下降段靠近最小弹速点某一时刻t2的输出频率推算初速和射角。弹道辨识总体方案如图3所示。

3 弹道辨识实现过程

基于总体方案，弹道辨识实现全过程如下:

1)确定相关参数、函数及定义域。

2)确定固定时刻t1和t2.时刻t1为在各种射击条件下位于涡轮发电机输出频率下降段且靠近炮口点的时刻，可利用试验获得;时刻t2为在各种射击条件下涡轮发电机均不发生停转且靠近最小弹速点的时刻，可利用仿真获得。

图3 弹道辨识总体方案Fig.3 Total scheme of trajectory discrimination

3)选取包含最大射角和最小射角在内的n1个射角θ0i{i =1，2，…，n1}，n1根据辨识精度要求确定。对应每个选取射角θ0i，通过弹道仿真平台，计算初速范围内不同初速v0下，t1时刻的弹速值v1，并拟合出v0与v1的函数关系，得到对应n1个射角θ0i的n1个关系式v0=φi(v1){i=1，2，…，n1}.

4)选取包含最大初速和最小初速在内的n2个初速v0j{j =1，2，…，n2}，根据辨识精度要求确定n2.对应每个选取初速v0j，通过弹道仿真平台，计算涡轮发电机在各种射击条件下不停转的最大射角至弹丸可能出现的最大射角范围内不同射角下t1和t2时刻对应的弹速值v1和v2，根据关系式k = (v1－v2)/(t2－t1)计算k(不直接用v2拟合，主要是减小后续计算误差)，并拟合出θ0与k 的函数关系，得到对应n2个初速v0j的n2个关系式θ0=φj(k){j =1，2，…，n2}.

5)对应每个选取初速v0j，通过弹道仿真平台，计算射角范围内不同射角下最小弹速值v3，并拟合出θ0与v3的函数关系，得到对应n2个初速v0j的n2个关系式θ0=φj(v3){j=1，2，…，n2}.

6)弹发射后，通过弹载频率测量设备测量涡轮发电机输出频率，记录t1和t2时刻涡轮发电机的输出频率值和最小输出频率值。

7)根据涡轮发电机最小输出频率判断涡轮发电机是否停转。涡轮发电机全弹道不停转时，执行步骤8)～步骤13);涡轮发电机弹道上存在停转时，执行步骤14)～步骤20).

8)根据t1时刻涡轮发电机的输出频率值和最小输出频率值，利用涡轮发电机输出频率与进气流的函数关系获取v1和v3.

9)利用v1、射角组θ0i中最小射角和最大射角对应的关系式v0=φ(v1)计算初速区间［v011v012］.

10)利用v3、初速组v0j中小于等于且最接近v011和大于等于且最接近v012的两个初速对应的关系式θ0=φ(v3)计算射角区间［θ011θ012］.

11)利用v1、射角组θ0i中小于等于且最接近θ011和大于等于且最接近θ012的两个射角对应的关系式v0=φ(v1)计算初速区间［v021v022］.

12)利用与步骤10)和步骤11)相同的办法，可计算出［θ021θ022］、［v031v032］、［θ031θ032］、….工程应用时，初速区间和射角区间计算次数应以保证必要的结果精度为宜。

13)根据最终计算出的初速区间和射角区间按照取区间中值或按线性分布计算等方法计算弹丸的初速和射角，完成弹道参量辨识。

14)根据t1和t2时刻涡轮发电机的输出频率值，利用涡轮发电机输出频率与进气流的函数关系获取v1和v2.

15)根据关系式k=(v1－v2)/(t2－t1)计算k.

16)利用v1、射角组θ0i中最小射角和最大射角对应的关系式v0=φ(v1)计算初速区间［v011v012］.

17)利用k、初速组v0j中小于等于且最接近v011和大于等于且最接近v012的两个初速对应的关系式θ0=φ(k)计算射角区间［θ011θ012］.

18)利用v1、射角组θ0i中小于等于且最接近θ011和大于等于且最接近θ012的两个射角对应的关系式v0=φ(v1)计算初速区间［v021v022］.

19)利用与步骤17)和步骤18)相同的办法，可计算出［θ021θ022］、［v031v032］、［θ031θ032］、….工程应用时，初速区间和射角区间计算次数应以保证必要的结果精度为宜。

20)根据最终计算出的初速区间和射角区间按照取区间中值或按线性分布计算等方法计算弹丸的初速和射角，完成弹道参量辨识。

说明:步骤1)～步骤5)为事先完成步骤，工程应用时，只将后续步骤用到的基础函数写入弹载微控制器;确定步骤1)中定义域时应留有余量。

4 实例仿真分析

基于上述弹道辨识方案及过程，在迫击炮弹上进行实例仿真分析。假定条件:初速变化范围76～89 m/s;射角变化范围43°～87°(在武器射角范围内考虑2°的跳动);涡轮发电机在各种射击条件下不停转的最大射角为72°;t1为1.5 s;t2为4.0 s;n1为45(两相邻射角相差1°);n2为14(两相邻初速相差1 m/s);用弹道方程组计算出的弹速代替实际应通过涡轮发电机输出频率获取的弹速。

1)确定45 个射角θ0i{i =1，2，…，45}对应的45 个拟合关系式v0=φi(v1){i=1，2，…，45}.

为便于计算，选择多项式拟合(以下同)。根据不同次数拟合误差及计算量确立拟合次数。

射角43°时，弹丸初速与飞行1.5 s 时速度的一次多项式拟合结果如图4所示，一次、二次、三次多项式拟合结果最大误差如表1所示。

图4 射角43°下初速与飞行1.5 s 速度的一次拟合曲线Fig.4 1° fitting curve of muzzle velocity and 1.5 s velocity under 43°angle of fire

从表1可以看出，拟合误差均较小，三次多项式拟合误差最小。综合考虑辨识精度、计算量和存储容量，选择一次多项式拟合。

表1 射角43°下初速与飞行1.5 s 速度的一次、二次、三次拟合最大误差Tab.1 1°－3° maximum fitting errors of muzzle velocity and 1.5 s velocity under 43°angle of fire

如表2所示，列举了不同射角下弹丸初速与飞行1.5 s 时速度的一次多项式拟合最大误差，初速拟合最大误差为0.004 m/s，说明一次多项式拟合满足要求。

表2 不同射角下初速与飞行1.5 s 速度的一次拟合最大误差Tab.2 1° maximum fitting errors of muzzle velocity and 1.5 s velocity under different angles of fire

2)确定12 个初速v0j{j=1，2，…，12}对应的12个拟合关系式θ0=φj(k){j=1，2，…，12}.

初速76 m/s 下射角与k 的一次、二次、三次多项式拟合结果最大误差如表3所示。

表3 初速76 m/s 下射角与k 的一次、二次、三次拟合最大误差Tab.3 1°－3° maximum fitting errors of angle of fire and k under 76 m/s muzzle velocity

从表3可以看出，三次多项式拟合误差最小，但将三次拟合系数取出(部分小数位被舍去)放到求解程序中求解射角时，求解误差比较大，达到0.8°.经多次仿真，选择求解误差小的二次多项式拟合。

3)确定12 个初速v0j{j=1，2，…，12}对应的12个拟合关系式θ0=φj(v3){j=1，2，…，12}.

初速76 m/s 时，射角与最小弹速的一次多项式拟合结果如图5所示，一次、二次、三次多项式拟合结果最大误差如表4所示。

图5 初速76 m/s 下射角与最小弹速的一次拟合曲线Fig.5 1° fitting curve of angle of fire and minimum velocity under 76 m/s muzzle velocity

表4 初速76 m/s 下射角与最小弹速的一次、二次、三次拟合最大误差Tab.4 1°－3° maximum fitting errors of angle of fire and minimum velocity under 76 m/s muzzle velocity

从表4可看出，三次多项式拟合误差最小，且满足研究需要，选择三次多项式拟合。

如表5所示，列举了不同初速下射角与最小弹速的三次多项式拟合最大误差，射角拟合最大误差为0.072°，说明三次多项式拟合满足要求。

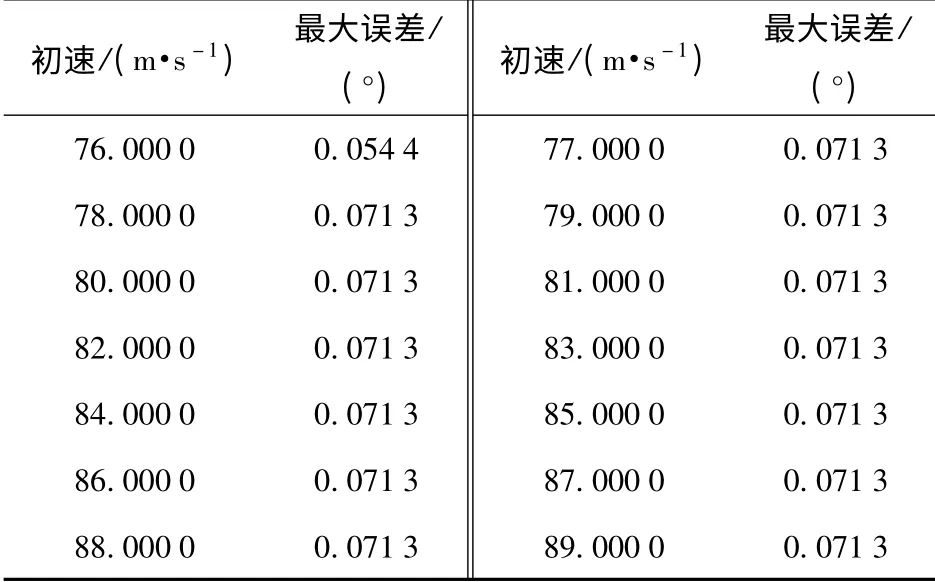
表5 不同初速下射角与最小弹速的三次拟合最大误差Tab.5 3° maximum fitting errors of angle of fire and minimum velocity under different muzzle velocities

4)辨识初速与射角。事先选定一组初速与射角，利用弹道方程组计算出弹丸飞行1.5 s 和4.0 s的速度和最小弹速，以此作为根据涡轮发电机输出频率获取的弹速，然后根据前述提及的弹道辨识过程辨识初速与射角。选定的初速与射角应覆盖假定初速与射角范围。如表6所示，列举了具有代表意义的初速与射角辨识结果，可看出，初速与射角辨识误差较小。

表6 初速与射角辨识结果Tab.6 Discrimination results of muzzle velocities and angles of fire

5 结论

将涡轮发电机作为速度传感器，提出了基于涡轮发电机输出频率的弹道辨识方法。利用该方法进行弹道辨识，计算量小，对弹载计算设备和存储设备要求低，适用涡轮发电机全弹道不停转和停转两种情况，加之涡轮发电机已在引信型号上应用，易于工程实现。初速与射角辨识结果表明:弹道辨识方法可行;参数n1、n2以及拟合关系式对弹道辨识精度、计算量和存储容量具有重要影响，应结合工程应用充分利用仿真手段予以优化。后续将针对利用涡轮发电机输出频率精确获取弹速和非标准气象条件下的辨识结果修正进行深入研究。

References)

［1］ 高敏，张强.迫击炮弹外弹道辨识方法［J］.探测与控制学报，2003，25(1):7－10.GAO Min，ZHANG Qiang.A method of trajectory identification for a mortar bomb［J］.Journal of Detection ＆ Control，2003，25(1):7－10.(in Chinese)

［2］ 王宝全，李世义，周国勇，等.基于弹道速度最小点的弹道辩识快速算法［J］.弹箭与制导学报，2002，22(4):48－52.WANG Bao－quan，LI Shi－yi，ZHOU Guo－yong，et al.A speedy method for trajectory recognition based on the minimum of trajectory velocity［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2002，22(4):48－52.(in Chinese)

［3］ 申强，李世义，李东光，等.一维弹道修正引信基于速度—时间序列的弹道辨识［J］.探测与控制学报，2004，26(1):41－44.SHENG Qiang，LI Shi－yi，LI Dong－guang，et al.A method of ballistic trajectory identification for CCF based on sequence of velocity－time［J］.Journal of Detection ＆ Control，2004，26(1):41－44.(in Chinese)

［4］ 万超，王伟，赵高波，等.基于速度－加速度测量的炮弹弹道辨识方法［J］.国外电子测量技术，2007，26(9):16－18.WAN Chao，WANG Wei，ZHAO Gao－bo，et al.Projectile trajectory identification methods based on speed and acceleration［J］.Foreign Electronic Measurement Technology，2007，26(9):16－18.(in Chinese)

［5］ 申强，葛腼，张冀兴，等.一种GPS 弹道辨识方法的精度仿真分析［J］.北京理工大学学报，2009，29(2):100－102.SHEN Qiang，GE Mian，ZHANG Ji－xing，et al.Analysis on the precision of a GPS－based trajectory identification method by simulation［J］.Transactions of Beijing Institute of Technology，2009，29(2):100－102.(in Chinese)

［6］ Philip F Ingersoll，Grosse Pointe Mich.Method of and apparatus for mortar fuze apex arming US 5390604［P］.1995－02－21.

［7］ 徐长江.引信侧进气涡轮发电机气动优化研究［D］.南京:南京理工大学，2007.XU Chang－jiang.Study of the aerodynamic optimization of the turbine alternator with side intake ducts for the fuze［D］.Nanjing:Nanjing University of Science and Technology，2007.(in Chinese)

［8］ 李福松，余春明，徐敏.旋转式气动发电机作为速度传感器探讨［J］.探测与控制学报，2007，29(3):21－24.LI Fu－song，YU Chun－ming，XU Min.Discussion on air driven revolving generator as velocity transducer［J］.Journal of Detection＆ Control，2007，29(3):21－24.(in Chinese)

［9］ 邓姚乾.迫弹速度特性与涡轮发电机输出［J］.探测与控制学报，2009，31(1):49－52.DENG Yao－qian.Analysis of velocity property for mortar shell in ballstic trajectory by an alternater test［J］.Journal of Detection ＆Control，2009，31(1):49－52.(in Chinese)

［10］ 宋承天，王克勇，郑链.迫弹引信涡轮电机模拟信号发生器设计［J］.仪器仪表学报，2008，29(3):614－617.SONG Cheng－tian，WANG Ke－yong，ZHENG Lian.Mortar fuze turbine alternator simulation waveform generator design［J］.Chinese Journal of Scientific Instrument，2008，29(3):614－617.(in Chinese)

［11］ 顾强，陶胜，安晓红，等.引信涡轮电机弹道信息的应用研究［J］.中北大学学报:自然科学版，2008，29(6):486－489.GU Qiang，TAO Sheng，AN Xiao－hong，et al.Application research on trajectory information of the fuze turbine generator［J］.Journal of North University of China:Science and Technology，2008，29(6):486－489.(in Chinese)