旋转弹头水平入水空泡及弹道的实验研究

顾建农，张志宏，王冲，范武杰

(1.海军工程大学 理学院，湖北 武汉430033;2.西安机电信息技术研究所，陕西 西安710065)

0 引言

随着破障炮弹、高速射弹研制的需要，以及“暴风雪”高速鱼雷在俄罗斯的成功应用，高速弹体的入水和水中弹道研究更是引起了各国的广泛兴趣，成为研究的热点问题。在足够高的入水速度下，由于伯努利效应引起弹体表面附近流体的压力降低，当该压力降至流体的饱和蒸汽压时，将在弹体表面产生空泡。当空泡数足够低时，空泡将会包裹整个弹体形成超空泡。在超空泡状态时，仅在弹头前端与水接触。当弹体速度降低时，空泡长度缩小，仅在弹头前端产生部分空泡，弹体尾端将与水介质接触。

由于空泡的产生和消失对弹体入水的运动阻力和水中弹道有重要影响，因此，掌握高速弹体水中运动的空泡形态和变化规律就成为解决高速弹体入水和水中弹道问题的基础和关键。对弹体姿态稳定、来流速度稳定的定常空泡，问题相对简单，可以进行理论分析或在水洞中进行实验和观察［1－4］。

与鱼雷、导弹运动特点不同，炮弹、火箭深弹等弹体入水除因旋转存在马格努斯效应外，还因入水速度高存在流体的压缩效应。因此，对旋转弹体高速入水的水中弹道研究，无论是理论上还是实验上都更加复杂。正是由于旋转高速弹体入水问题的复杂性，发展一种半理论、半经验的工程近似方法不失为一条解决实际问题的途径，根据实验结果确定弹体入水空泡分离的位置及其形状，再应用理论的方法来预测弹体的入水弹道［5］。

本文利用数字式高速录像实验研究了两种制式弹头在两个水深时6 种速度下水平入水时的空泡及弹道特征。

1 实验设备

实验设备由入水水箱、制式枪弹、发射装置和水中弹道测量系统4 部分组成。

1.1 入水水箱

为弹头入水实验设计建造的水箱尺寸为4 m ×1 m ×2 m.水箱骨架为角钢结构，底板为钢板。水箱四周是防弹玻璃，以便有利于拍摄弹头的入水弹道，而且还能承受较大的弹头撞击力和水箱中的静水压力，以防损坏和变形。

1.2 制式枪弹

实验中采用9 mm 弹道枪作为发射装置，枪管长88.63 mm，缠度所发射的弹头分别为9 mm 制式手枪弹头与头部形状为半球形的弹头，其发射速度依据装药量的不同从137 m/s 到400 m/s分6 个等级变化。手枪弹头的质量为8 g，弹头长15.8 mm，弹头壳材料是91 铜，弹心材料为含5%锑的铅锑合金。球形弹头的质量为6.2 g，弹头长13.26 mm，弹头材料为黄铜。弹道枪、弹与弹头的实物照片如图1所示。

1.3 水下水平发射装置

图1 弹道枪、枪弹与弹头Fig.1 Trajectory gun，cartridge and bullet

在水箱右侧面距箱底0.5 m 处开有水下射击孔，孔径20 mm，为防止水从射击孔外泄，同时不干扰枪弹从射击孔的射入，在射击孔口处装有厚度约为0.1 mm 的薄膜胶片，每次射击破膜后需更换新的膜片。在射击孔右侧装有水平射击平台，用于固定弹道枪，确保枪膛轴线与射击孔中线在一条直线上。弹道枪出口与射击孔的边沿有20 mm 空隙，让射击时枪膛内的高压烟气向空气中散去，防止它们冲入水箱中，以免影响弹头水中弹道与空泡的观察。

1.4 水中弹道拍摄测量装置

采用KODAK 公司生产的KODAK4540MX 数字式高速录像系统测量弹头水中弹道。该高速录像系统的像素为256 像素×256 像素，灰度为256 级。最高记录速度为满幅4 500 幅/s，分幅40 500 幅/s.

为了能方便地从录像中判读出入水弹头的运动轨迹，在水箱中沿射击轴线偏右0.08 m 处的铅垂平面上均匀布置了白色坐标网格线，垂直网格线间距为0.1 m，在每根垂线上每隔0.1 m 用黑色胶带缠上做了记号。这样布置网格坐标线的好处是一方面它的存在不会干扰水中弹头的运动，另一方面在录像对焦时可保证弹头与坐标线图像都清晰，同时还可尽量减小由于视差带来的判读误差。坐标网格线在水箱中的布置及弹道枪的水平安装如图2所示。

图2 坐标网格线及弹道枪Fig.2 Grid line and the trajectory gun

高速录像对光源的要求较高，为此在水箱后离水箱后壁1 m 处悬挂了一大张白色幕布，在布后布置了3 盏双连装的新闻灯，每支灯管1 000 W，共6 000 W以保证录像时网格坐标线背景能看得较清晰，在水箱前面布置了一盏2 000 W 的双连装新闻灯，通过它直接照射到入水弹头与空泡面上，可较清晰地看到空泡的形状。弹头入水实验方案如图3所示。

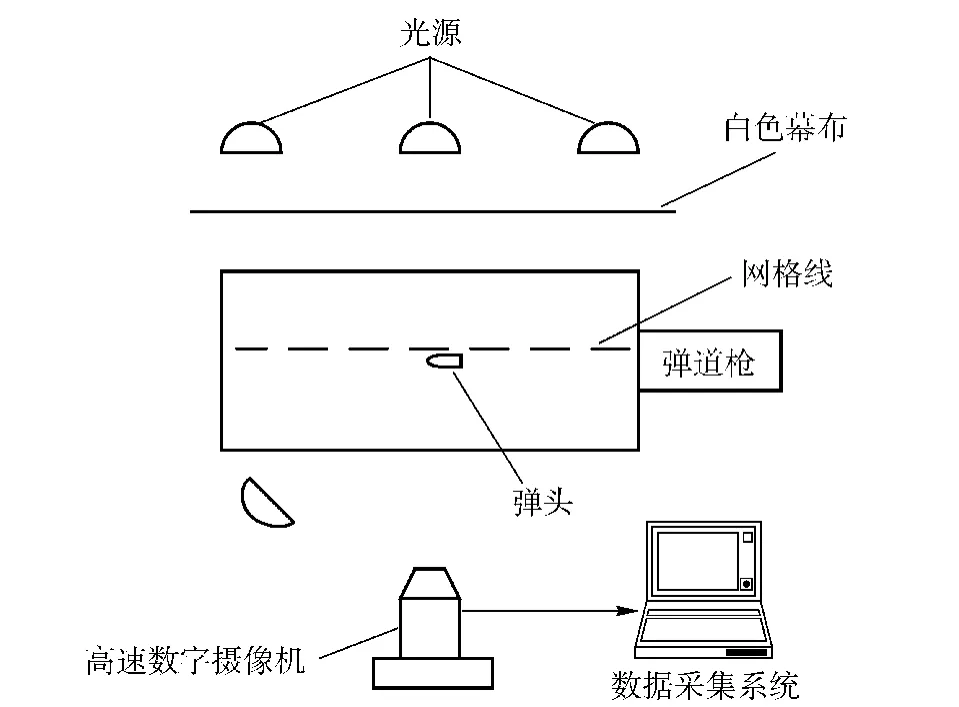
图3 弹头入水实验方案Fig.3 Scheme of bullet water－entry experiment

2 实验结果与分析

利用上述实验设备在水箱中进行了旋转弹头的水平入水实验。实验进行了两个水深:射击孔中心距水面的高度分别为0.5 m 与1.0 m，两种弹型:半球头、普通制式弹头，6 种速度:137.9 m/s、204.2 m/s、246.9 m/s、303.4 m/s、358.4 m/s、401.7 m/s 的弹头水平入水射击实验拍摄记录。对于每种弹头的运动状态均进行了全弹道的记录与局部运动状态的放大记录。

2.1 弹头水平入水空泡

当弹头从箱体外水平发射，弹头破膜后进入水箱中，其空泡发展分为4 个阶段:开空泡、空泡闭合、颈缩、溃灭。如图4所示，详细地给出了水下水平射击孔口中心距水面0.5 m，半球形弹头水平入水速度为358.4 m/s 时弹头入水初期空泡的发展过程。从这一系列图片可以看出，在弹头刚入水不久，空泡为开空泡，形状对称，空泡壁面光滑透明，表明此时弹头的运动姿态较好。在经过了1.22 ms 后，可以看到空泡壁面明显地开始右旋(图4(d))，随即右旋型空泡壁面开始变得粗糙，其右旋的速度约为100 r/s.空泡壁面这种右旋的出现并不是由于弹头绕自身轴旋转造成的(在入水速度为358.4 m/s 时，根据弹道枪膛线缠度为右旋254 计算得弹头绕轴旋转速度为156.8 r/s)，而是由于弹头入水后，在空泡中运动时，其上会受到一个不稳定力矩导致弹头在空泡中翻滚所引起的，有时也会观察到向左旋转的空泡壁面，如图5所示。

图4 半球形弹头的空泡发展过程Fig.4 Developing process of half sphere pistol bullet cavity

图5 普通制式弹头空泡壁面左旋Fig.5 Cavity surface which the general pistol bullet rotates left

如图6所示，比较了在水下水平射击孔口中心距水面0.5 m，弹头水平入水速度为400 m/s，入水时间为7.11 ms 时两种弹型(半球形、普通制式)在同一发射状态下的空泡形态比较。可看出普通制式弹头由于弹形的缘故，表现出特有的“藕节”型空泡，其弹道也不稳定，表现出一定的随机性。

如图7所示，比较了半球形弹头水平入水速度为358.4 m/s，入水时间为7.56 ms 时，在发射孔距水面不同深度处(1.0 m 与0.5 m)空泡形态的比较，可看出这2 种发射状态的空泡形态变化不大，这一结果是可以理解的，因为由于水深的变化(相差0.5 m)而导致的环境空泡数的变化不到5%.

图6 两种头型弹头空泡形态比较Fig.6 Comparison between the half sphere and general pistol bullet cavity

图7 两种水深时半球型弹头空泡形态比较Fig.7 Comparison of the half sphere pistol bullet cavity between the two depths of water

文献［6］在研究鱼雷垂直入水的空泡外形时认为除了弹体头部附近以外，入水初期空泡几乎为一精确的抛物面，理论上的预测和实验测量给出了垂直入水的空泡外形，可近似写成(1)式:

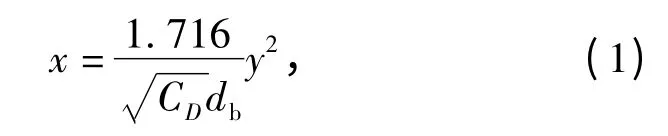
式中:db为弹体截头直径或为具有连续变化曲线的其他头型的最大直径;CD为带空泡航行体的阻力系数，其中:D 为弹体运动阻力，ρ 为流体密度，v0为弹体运动速度为弹体特征面积。

对于高速射弹水平入水，由于弹体入水速度大，在入水初期可以忽略重力对空泡形态的影响，因而可以利用垂直入水的空泡外形计算式(1)式计算水平入水的初期空泡，计算结果如图8所示。曲线B为图4系列空泡中的外形(入水速度358 m/s、入水时间0.77 ms)，曲线A 为(1)式计算的空泡外形，计算中取CD=0.247，db=9 mm.由计算结果和实验结果的比较知道，二者有较好的吻合，因此可以利用(1)式对球型弹头的初期入水空泡进行预报。

2.2 水平入水弹头的弹道及速度衰减规律

图8 弹体入水早期空泡外形Fig.8 Cavity shape of sphere pistol bullet at the initial time after it entraining water

如图9所示，给出射击孔心距水面0.5 m，速度为303 m/s 时，半球形弹头与普通制式弹头两种弹型水平弹道轨迹比较。水平入水的弹头由于在空泡内的翻滚导致自身运动的不稳定，因而它们的运动轨迹不是沿直线运动。如图10 所示，给出了射击孔心距水面0.5 m 速度为303 m/s 时，半球形弹头与普通制式弹头两种弹型的速度衰减规律的比较，如图11 所示，为射击孔心距水面0.5 m，制式弹头水平入水时，两种初始速度的弹头入水速度衰减规律的比较。从这些图中可看出，弹头的入水速度衰减规律似乎与速度无关，而对于半球形与普通制式弹头这两种弹头的速度衰减规律也较一致，表现出很强的相似性，都呈现出极强的速度衰减特性，表明入水弹头在入水后不久其速度就很快地衰减了。

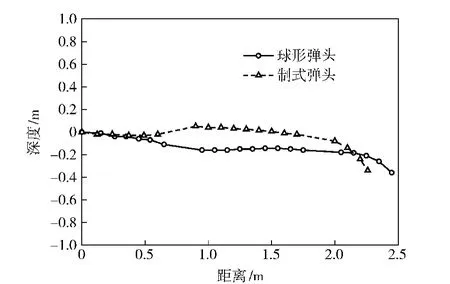
图9 两种弹型水平弹道轨迹比较Fig.9 Comparison between the sphere and general pistol bullet ballistic trajectory

弹头入水后的速度衰减规律可由(2)式给出。如模型入水速度为v0，弹头最大横截面积为A，质量为m，假定入水初期阻力系数CD保持为一常数，不计重力与浮力，则一个简化的弹头运动方程为

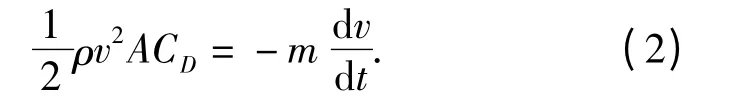
令

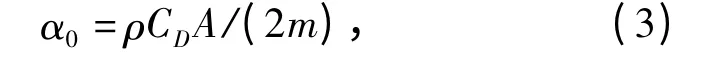
式中α0称为减速系数。

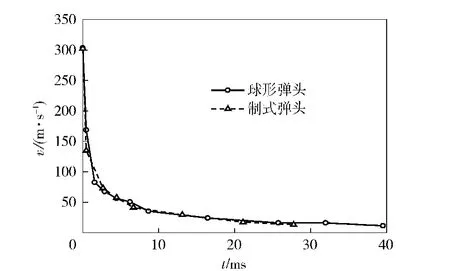
图10 两种弹型的速度衰减规律的比较Fig.10 Comparison of pellet velocity attenuation law between the sphere and general pistol pellet

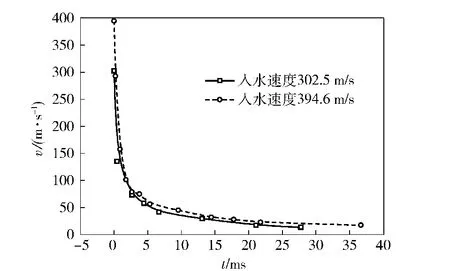
图11 两种初速下弹头速度衰减规律的比较Fig.11 Comparison of the pistol bullet velocity attenuation law between two kinds of initial speed积分(2)式，得

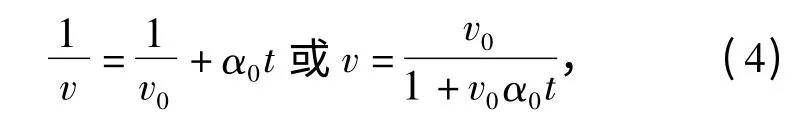
式中:t 为弹头入水以后的时间;v 为对应入水时刻t的速度。

考虑半球形弹头水中运动翻转情况，取半球形弹头直径与长度之和的1/2 作为当量直径，即取d=11.15 mm，经过试算取CD=0.394.则由

m=6.2 ×10－3kg，A=πd2=9.76 ×10－5m2，有α0=ρCDA/(2m)=3.1.

对半球形弹头入水情况，利用(4)式计算弹头水中运动速度随入水时间的变化规律，在计算结果与实验结果之间显示了较好的一致性，如图12 所示，这也说明弹头的平均阻力系数为0.394.

3 结论

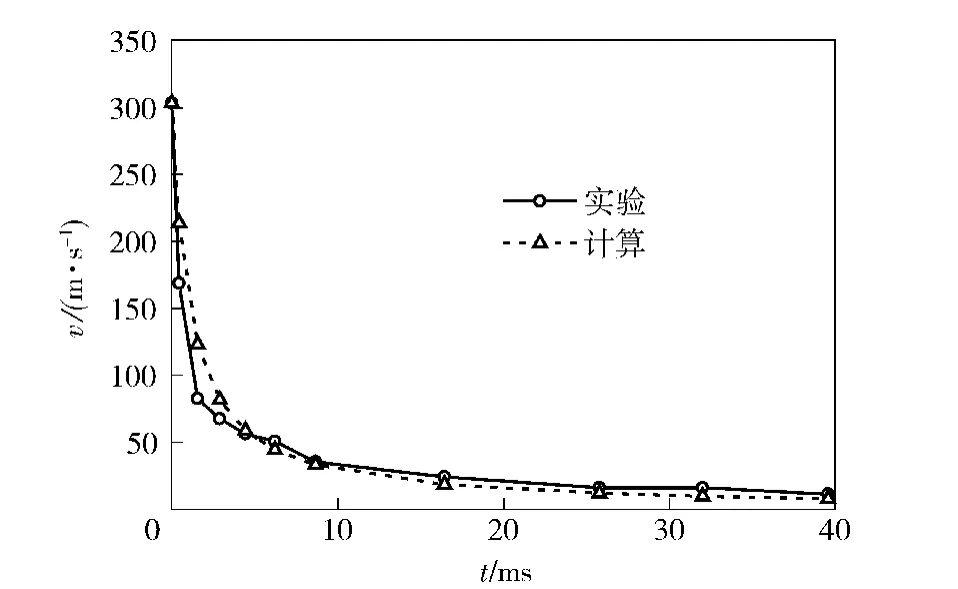
图12 弹头水中速度衰减规律实验与计算的比较Fig.12 Comparison of the half sphere bullet velocity attenuation law between experiment and calculation

对实验结果的分析表明，弹头形状对入水弹道的稳定性及空泡形状有着重要影响。对于半球形与普通制式弹头这两种弹型，普通制式弹头表现出特有的“藕节”型空泡，其弹道也不稳定，表现出一定的随机性。而半球形弹头在入水时相对于普通制式弹头表现出较好的弹道稳定性。高速水平入水弹头的早期空泡形状近似为抛物形。

在一定的速度范围内，弹头入水的速度衰减规律具有一定的相似性。且表现出极强的速度衰减特性。

通过理论分析，建立了弹头水中速度与入水时间关系的数学预报模型，并与实验结果进行了比较，理论与实验结果显示了较好的吻合。

References)

［1］ 安波，蒋建伟，蒋浩征.高速钢球对水介质侵彻时瞬时空腔形成的数值模拟［J］.爆炸与冲击，1998，18(3):245－250.AN Bo，JIANG Jian－wei，JIANG Hao－zheng.The numerical simulation of the temporary－cavity forming during the high－velocity steel－ball penetrating into water medium［J］.Explosion and Shockwaves，1998，18(3):245－250.(in Chinese)

［2］ Vorus W S.A theoretical study of the use of supercavitation/ventilation for underwater body drag reduction［R］.Osaka:VAI，1991.

［3］ Varghese A N，Uhlman J S，Kirschner I N.High－speed bodies in partially cavitating axisymmetric flow［C］∥5th International Symposium on Cavitation.Osaka:CAV，2003:1－5.

［4］ Vlasenko Y D.Experimental investigation of supercavitation flow regimes at subsonic and transonic speed［C］∥5th International Symposium on Cavitation.Osaka:CAV，2003:6－13.

［5］ 顾建农，张志宏，范武杰，等.旋转弹体入水弹道的计算方法［J］.海军工程大学学报，2001，13(4):1－7.GU Jian－nong，ZHANG Zhi－hong，FAN Wu－jie，et al.The hydroballistic calculation method for the water entry of a rotary projectile［J］.Journal of Naval University of Engineering，2001，13(4):1－7.(in Chinese)

［6］ May A.Water entry and the cavity－running behavior of missiles ADA020429［R］.Maryland:White Oak Laboratory，1975.