波浪对导弹垂直发射水弹道影响研究

王亚东，袁绪龙，张宇文，刘维

(西北工业大学 航海学院，陕西 西安710072)

0 引言

潜射导弹以其隐蔽性等优势为各大军事强国所重视。由潜艇发射后，导弹需要跨越水介质至空中再进入预定弹道。在水下航行过程中，导弹会受海洋表面波浪的影响运动参数会产生扰动，参数变化导致导弹出水后空中弹道初始条件不可预测，较差的条件甚至会导致导弹发射失败。

目前对水下潜体［1－2］和水面舰船及其海洋结构物［3－5］的波浪力研究比较充分，也获得了一定的试验数据［6］。但对于潜射导弹等跨介质武器的波浪扰动效应研究仍鲜有文章发表，特别是未针对地给出导弹在不同深度下波浪影响程度大小。

本文采用双叠加模型，以Pierson－Moscowitz 谱和SWOP 方向分布函数为基础建立随机波浪数学描述，使用切片法求解导弹所受波浪扰动力。仿真了波浪对导弹出水运动参数的影响，并就海况、海浪主浪向等参数变化时波浪对导弹影响的差异进行了研究，给出了这些参数影响的变化趋势。

1 数学模型

1.1 基本假设

海浪运动是空间和时间上均不规则的随机运动，且海浪受边界条件和外界扰动等诸多因素影响。为了研究问题方便，需要对实际海浪做以下假设［7］以利于模型建立:

1)流体是不可压缩的、理想的;

2)流体的深度是无限的;

3)导弹的直径和波长相比为小量，可做长波近似。

1.2 波浪模型

19世纪40年代开始，出现了用随机过程来研究海浪的方法，即谱分析法。大量的理论分析和观测结果证明海浪可以用窄频带谱的正态随机过程来描述，在此基础上人们提出了许多描述波浪的模型，其中应用较为广泛的为Longuet－Higgins 模型以及考虑方向谱的双叠加模型。

Longuet－Higgins 模型认为海上某一固定点(x0，z0)在t 时刻波面高度由许多个余弦波叠加而成，由下式表达:

式中:An，ωn，kn，εn分别表示第n 个余弦组成波的振幅、圆频率、波数和初始相位;γ 为浪向角;(x0，z0)为空间位置;t 为时间。其中εn取0～2π 范围内均匀分布的随机数。

上述模型仅考虑了主风向上的海浪，但实际的海浪是由来自多个方向的一系列波浪混合而成，考虑方向，采用如下双叠加模型:

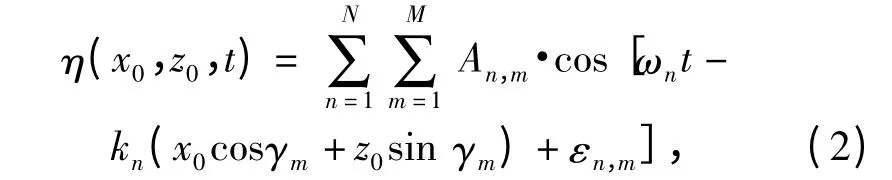
根据频谱分析，可知An，m满足以下关系:

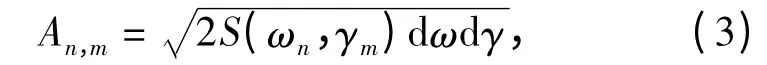
式中S(ω，γ)称为谱能密度，其表达方式如下:

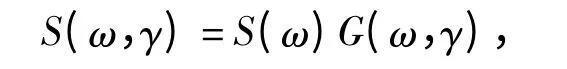
式中S(ω)和G(ω，γ)分别为波浪频谱和方向分布函数。

目前较常见的海浪频谱有Bretschneider 谱、Pierson－Moscowitz(P－M)谱、JONSWAP 谱和Neumann谱。P－M 谱为经验谱，其依据的资料比较充分，分析方法合理，在海洋工程和船舶工程中使用广泛，本文使用该频谱进行计算，其表达式［7］为:

式中:vw为自由表面以上19.5 m 标准高度处的风速;C1，C2为无量纲参数，最常用的值为C1=8.1 ×10－3，C2=0.74;g 为重力加速度。

方向分布函数选用波浪立体观测计划SWOP的公式:

式中:p，q 为中间变量，其求解方法为p = 0.5 +其中谱峰频率ωmax由频率谱S(ω)对频率的偏导数为0 求得:

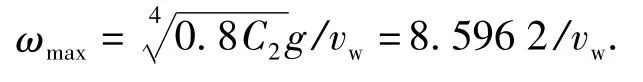
于是根据(3)式，离散化得:

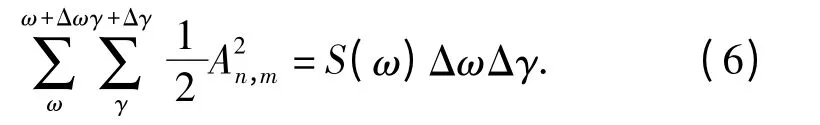
采用复数来表示以上结果，可得:

式中φ'0为临时变量。

利用上述数学模型构建仿真所需的随机波浪，频率区间取30 份、浪向角区间取36 份，得4 级海况下海浪分布如图1所示，显示了描述随机波浪的离散波浪幅值在频率、浪向角上的分布。

1.3 波浪力计算模型

波浪对导弹的力可分为由波浪运动引起的附加压力场作用于弹体表面的定常力及波浪非定常运动导致的惯性力两部分。将波浪复势利用坐标变换转置导弹体坐标系内，可分别求解上述两种类型力。

波浪在水下产生的附加压力场为

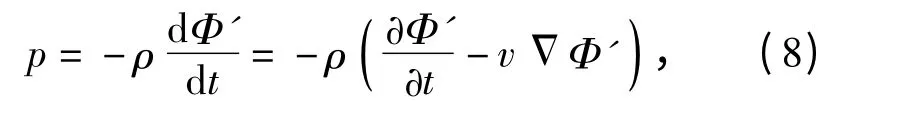
式中:v 为导弹的速度;ρ 为流体密度。

该压力场对单位长度的切片产生的在导弹体坐

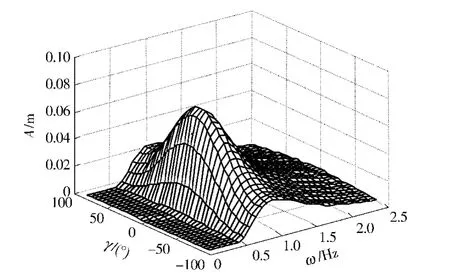
图1 波浪幅值分布Fig.1 Distribution of wave amplitude

标系y、z 方向的力为:

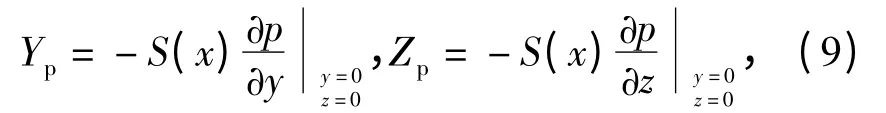
式中，S(x)为导弹某切片的横截面积。

波浪运动中，水下的流体质点作非定常运动，这将对导弹产生附加惯性力。导弹单位长度切片在体坐标系y、z 方向的附加惯性力为:

式中:v'y，v'z为切片中心处流体质点由于波浪产生的在体坐标系y、z 方向的扰动速度;Sey(x)，Sez(x)为单位长度切片的附加质量。

以上得到了导弹各切片在波浪作用下的压力场力和附加质量力。由此可得导弹体坐标系中总的力和力矩为:

式中，取Y，Z，My，Mz的实部即为波浪运动作用在导弹体坐标系下的力和力矩。

(11)式离散化后，可采用切片法求解。切片的原则为在头部、尾部形状变化较大处切分较细;在平行中体可适当减小切分份数。一般说来，切片总数增加可以提高计算精度，实际计算表明，切片总数达到90 左右，切片个数对波浪力计算精度的影响己可忽略不计。每一切片横截面的扰流可局部地看作二元流动，切片的附加质量与几何形状有关，简单的二元附加质量系数可根据无限长圆柱附加质量系数用保角变换求出。

1.4 水弹道方程

潜射导弹水弹道方程由动力学方程组和运动学方程组组成，其中动力学方程组根据动量和动量矩定理建立，如(12)式所示:

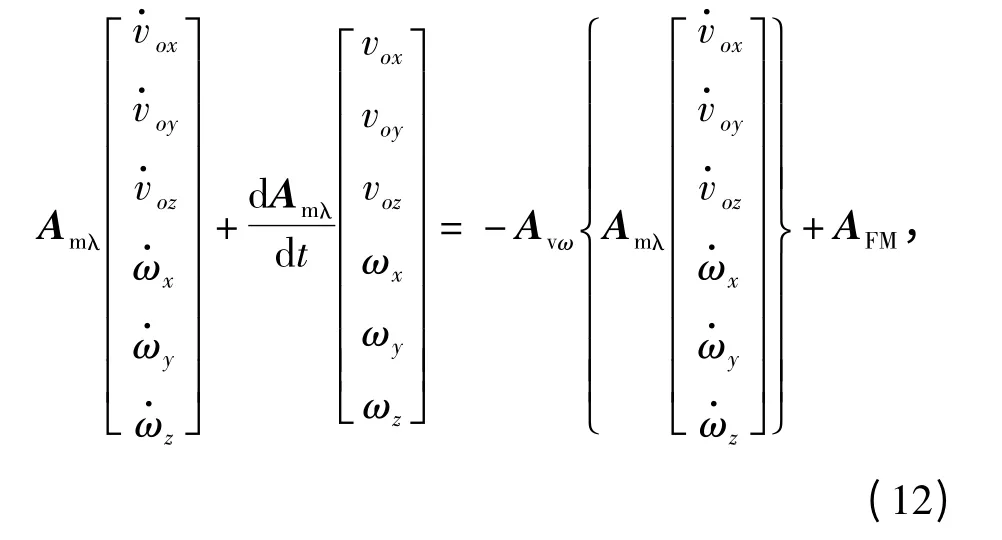
式中:Amλ为惯性矩阵;Avω为速度矩阵;AFM为力矩阵。

导弹的运动描述为浮心平动和弹体转动，平动方程组如(13)式所示:

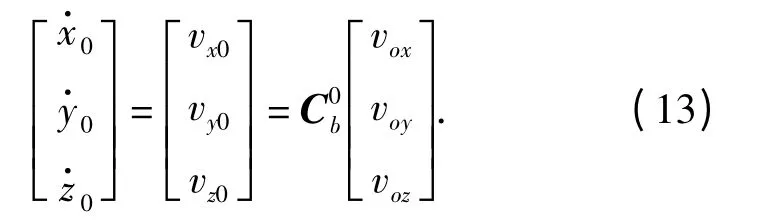
弹体转动方程如(14)式所示，描述θ，ψ，φ 三个欧拉角的变化(使用反欧拉角定义以避免垂直发射引起的角度奇异):

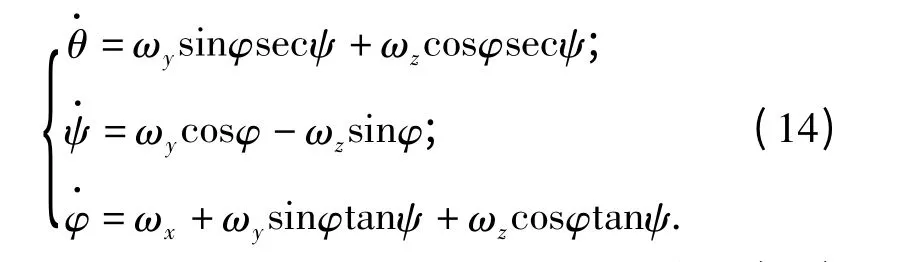
再加上攻角α、侧滑角β 和速度v 的定义(15)式:

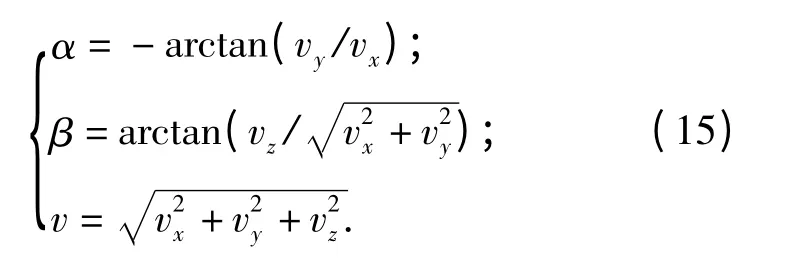
联立(12)式～(15)式可得潜射导弹水下弹道方程组。

2 仿真结果

2.1 统计方法

本文主要考查波浪对水下垂直发射、无控制导弹弹道参数影响，研究方法为计算无波浪作用下标准弹道和存在波浪扰动弹道，求得波浪扰动下参数偏差来探究影响大小。

实际中充分发展的波浪是一个各态历经的随机过程，在出水运动过程中作用在导弹上的波浪相位、主浪向等参数不尽相同，如图2所示。而工程中最关心的是导弹运动经过某一深度时特定参数在有无波浪条件下极限偏差大小以判定波浪影响是否可以接受，因此对于导弹垂直发射弹道波浪影响的个例计算意义不大。

图2 导弹与波面相对位置关系Fig.2 Relative positions between missile and wave surface

为解决以上问题，本文采用统计学方法获取波浪对导弹垂直发射水弹道影响，借鉴蒙特卡洛法思想，利用随机数序列生成不同初始参数波浪进行仿真，以构造真实中弹体和波面的各种不同位置，进而分析波浪对参数极限偏差的影响。此法需要对同一工况进行大量计算，计算次数的选择根据预试获取，本文选用200 次计算，经校验:200 次计算和800 次计算结果误差很小，保证了计算结果的代表性和经济性。

结果分析方法:对于多次计算结果的各个运动参数，均减去不考虑波浪影响的标准弹道相应位置处的参数得到参数偏差，而后对于弹道中对应的每个深度位置取200 条弹道参数偏差的最大值，绘制参数偏差量最大值随深度变化曲线，给出海浪影响在弹道不同深度下的最大扰动。该图表给出了导弹在出水过程中经过的各个深度下弹体运动参数受波浪影响的偏差极值。

波浪对导弹水弹道的各项参数均有影响，本文取某口径导弹为计算对象，就垂直发射离艇至出水过程中所关心的攻角、俯仰角速度、偏航角速度等值从海况级别影响、海浪主浪向影响等方面探究波浪对导弹水弹道影响。

根据以上研究目的，制订计算工况如表1所示。

表1 计算工况Tab.1 Calculating Conditions

2.2 波浪对运动参数影响规律

取表1中编号2 对应工况，考究波浪作用下导弹运动参数相对无波浪标准弹道的偏差，并分析不同深度下偏差大小关系。

仿真结果表明波浪作用下导弹各项运动参数均发生了改变，且参数偏差随导弹深度减小显著增大。此处列出该工况下影响较大的几个参数偏差随深度(定义水下深度为负值)变化曲线。

如图3所示，在波浪作用下导弹运动参数最大偏差随深度均满足三次多项式关系，深度减小，参数偏差显著增大，在导弹近水面时达到极值，该规律验证了波浪能量的表面性。

2.3 海浪参数影响分析

由2.2 节可知，在波浪作用下，导弹运动参数在不同深度下的最大偏差呈三次多项式关系，在近水面处达到最大，弹道设计时最关心的是整个水下弹道参数受波浪影响的最大值，以确定弹道品质是否符合要求。本节针对常用的波浪参数进行了仿真，给出了各条件对应的弹道参数偏差最大值，以供设计人员参考。

首先取导弹典型初始速度15 m/s，发射艇速2 kn，分别计算3、4、5 级海况下导弹从水下30 m 发射至头部触水过程，列出不同海况下参数最大偏差在导弹头部触水时刻值，如表2所示。

表2 不同海况下偏差最大值Tab.2 Max parameter deviations vs.sea level

如图4所示，很明显海况级别越高，对弹道参数偏差影响程度越大，且参数最大偏差值与海况呈近似线性关系。因为海况越高，波浪引起的流体微元运动越剧烈，作用在导弹上的附加压力场和附加惯性力也越大。该系列计算的波浪方向为迎浪，故海况越高，波浪力作用越大，引起的附加攻角和俯仰角速度也就越大。

变更主浪向，以获得不同方向入射的波浪对导弹水弹道参数影响。前述仿真结果海浪均为0 度主浪向(迎浪)，此处仍以15 m/s 发射速度，2 kn 发射艇速，4 级海况为基础，计算主浪向角分别为0°、45°(首斜浪)、90°(横浪)导弹发射至头部触水过程，获得不同主浪向下参数最大偏差在导弹头部触水时刻值，如表3所示。

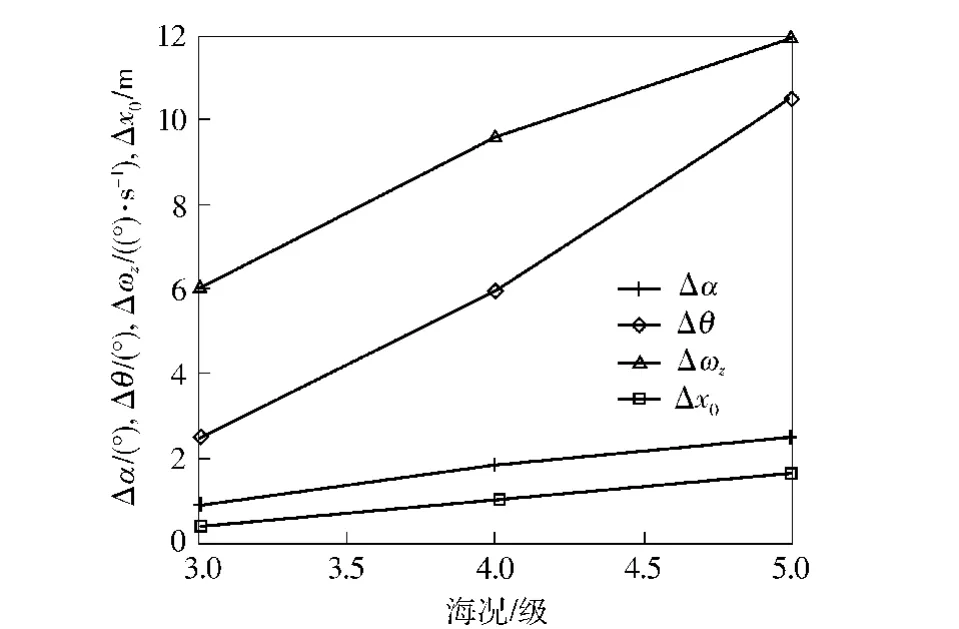
图4 参数最大偏差随海况变化Fig.4 Max parameter deviations vs.sea level

表3 不同主浪向下偏差最大值Tab.3 Max parameter deviations vs.main wave direction

从偏航运动参数差异判别主浪向角影响，如图5所示，随着夹角增大，波浪对导弹偏航参数影响增大，90°主浪向角入射使导弹水弹道参数偏离无波浪导弹程度最大。波浪主浪向决定波浪对弹体作用的主方向，迎浪引起的攻角偏差和俯仰角速度偏差最大，横浪引起的侧滑角偏差和侧向偏距最大。弹体位置和姿态确定的情况下，弹体各向参数受波浪作用取决于波浪入射角度。

图5 参数最大偏差随主浪向变化Fig.5 Max parameter deviations vs.main wave direction

3 结论

波浪作为扰动源作用在水下运动的导弹上会影响弹道品质，特别对于无控导弹，波浪会造成较大的出水参数偏差，有必要最大程度真实地模拟波浪作用。常规波浪力计算通常只考虑单方向入射的随机波，计算结果偏于保守，为了使弹道满足要求，需要较大的设计裕度，增加了成本及实施难度。

本文采用P－M 频谱，增加了SWOP 方向谱来构建更趋近于现实的波浪数学描述，采用切片法计算波浪扰动力。利用该成熟算法结合蒙特卡洛思想用统计方法计算波浪扰动引起的参数最大偏差，并给出了不同海况、主浪向条件下波浪扰动引起的参数偏差极值，结论如下:

1)海浪扰动作用在弹体上会引起可观的参数偏差，导弹头部触水时刻4 级海况波浪引起的攻角偏差可达1.9°，俯仰角偏差达5.97°，出水位置偏距达1.1 m;

2)统计方法得到的弹道最大参数偏差随深度变化满足三次多项式关系，波浪作用随水深减小显著增大;

3)海况越高，波浪对参数偏差影响越大，受影响的主参数偏差数值随海况增加呈近似线性增大趋势;

4)主浪向决定了波浪能量的主作用方向，主浪向方向上的弹体运动参数受影响最大，影响程度随角度呈近似线性衰减/增加趋势。

References)

［1］ 匡晓峰，汪玉，缪泉明，等.水下航行体波浪力理论预报［J］.船舶力学，2006，10(1):28－35.KUANG Xiao－feng，WANG Yu，MIAO Quan－ming，et al.Theory prediction of wave forces for a deep－submerged body［J］.Journal of Ship Mechanics，2006，10(1):28－35.(in Chinese)

［2］ 冯学知，蒋强强，缪泉明，等.潜体波浪中近水面不同潜深和航向时运动和波浪力计算［J］.船舶力学，2002，6(2):1－13.FENG Xue－zhi，JIANG Qiang－qiang，MIAO Quan－ming，et al.Motion and wave forces calculation of a deep－submerged body in different depth and course near water surface［J］.Journal of Ship Mechanics，2002，6(2):1－13.(in Chinese)

［3］ Barbaro G.A new expression for the direct calculation of the maximum wave force on vertical cylinders［J］.Ocean Engineering，2007，34(11－12):1706－1710.

［4］ 秦洪德.船舶运动与波浪载荷计算的非线性方法研究［D］.哈尔滨:哈尔滨工程大学，2003.QIN Hong－de.Nonlinear method for the computation of ship motions and wave loads［D］.Harbin:Harbin Engineering University，2003.(in Chinese)

［5］ 冯波，郑永红，游亚戈，等.大深度分层流体中二维淹没浮体的波浪力分析［J］.海洋学报，2008，30(1):156－162.FENG Bo，ZHENG Yong－hong，YOU Ya－ge，et al.Wave forces acting on a submerged floating body of two－dimensions in layered fluid with greater depth［J］.Acta Oceanologica Sinica，2008，30(1):156－162.(in Chinese)

［6］ 冯学知，缪泉明，蒋强强，等.潜体近水面波浪力试验研究［J］.船舶力学，1997，1(2):24－28.FENG Xue－zhi，MIAO Quan－ming，JIANG Qiang－qiang，et al.The experiment analysis for wave forces of a submerged slender body running near the free－surface in regular waves［J］.Journal of Ship Mechanics，1997，1(2):24－28.(in Chinese)

［7］ 张宇文.鱼雷弹道与弹道设计［M］.陕西:西北工业大学出版社，1998.ZHANG Yu－wen.Torpedo ballistics and ballistics design［M］.Shaanxi:Northwestern Polytechnical University Press，1998.(in Chinese)