基于垂直矢量阵的相干信号方位估计算法

卞红雨，王珺琳

(哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨150001)

0 引言

由于大多水下潜器对于目标探测的分辨率要求较高，因而高分辨算法的研究一直是科研热点。在主动探测过程中，相干信号是普遍存在的，而大部分高分辨算法必须进行空间平滑［1］等预处理才可以实现解相干，并且需要预估信号源的数目。计算到达角瞬态成像(CAATI)［1］算法通过扩展的prony 方法［2］拟合各阵元的输出，在高信噪比的条件下，只需很少的基元和快拍数，就可以准确获得多个目标(相干或非相干)回波的幅度以及方位信息，运算量小，运算速度快，并且在侧扫声纳中得到了一系列的应用［3－4］。针对其高信噪比门限，文献［5－6］提出了一些解决方法。近年来已有学者尝试将其应用到前视声纳中［7］。

由于CAATI 算法对信号形式的高要求，现有研究都是将其应用于声压阵列信号处理，故只能得到目标的水平或垂直信息。实际应用中，为了确保水下潜器的安全航行，需要精确知道水下潜器运行前方是否存在障碍物以及障碍物的具体位置，而利用一维矢量阵即可实现目标的空间方位估计，矢量传感器由于其自身的优越性能［8］，已经在水声领域扮演越来越重要的角色。因此文中将CAATI 算法引入垂直矢量阵测向处理中，可以有效地实现相干信号源的空间方位估计，并且避免了文献［9］中所述的参数配对问题。

矢量阵CAATI 算法无论在水平维还是垂直维可同时解算的相干源数目十分有限，因此在实际的海洋环境中，矢量阵CAATI 算法的模型不适于解算诸如海底一类被看作由无限点源组成的目标，而对于点源或由有限点源组成的目标，该算法有很好的分辨效果。若将该方法用于小型避障声纳中，由于避障声纳的主要任务是探测航行器前方的目标情况，所以为保证发射波束尽量避免打到海底(或海面)，其发射波束的垂直开角较小且探测距离有限，这种情况下，利用文中方法不仅可以获取前方目标的空间方位，而且有效的降低了硬件要求。此外，该方法也可以用于探测水雷等水中悬浮目标。

1 矢量阵CAATI 算法原理

矢量阵CAATI 算法实现框图如图1所示。

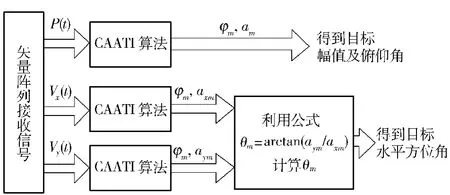
图1 垂直矢量阵CAATI 算法实现框图Fig.1 Diagram of CAATI arithmetic using a vertical vector sensor array

1.1 矢量阵列数据模型

采用经典的矢量阵列数据模型［10］。假设有M个窄带平面波信号通过一个空间各向同性、静止的均匀液体，入射到K 元矢量传感器阵上，且第m 个信号的方位为Ω=(θm，φm)，其中θm为水平方位角(与x 轴夹角)，φm为俯仰角(与xoy 平面夹角)，则信号源(假设为点源)的方向矢量um= (cos φm，cos θm，cos φmsin θm，sin φm).以第一个基元为参考点，设矢量阵列中第k 个阵元的空间位置为(xk，yk，zk)，k =1，2…K.则第k 个阵元相对于参考阵元的延时为［11］:

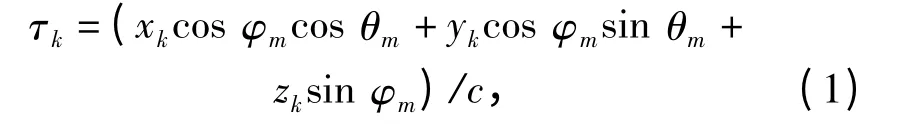
式中c 为声速。

则第k 个基元的输出为:

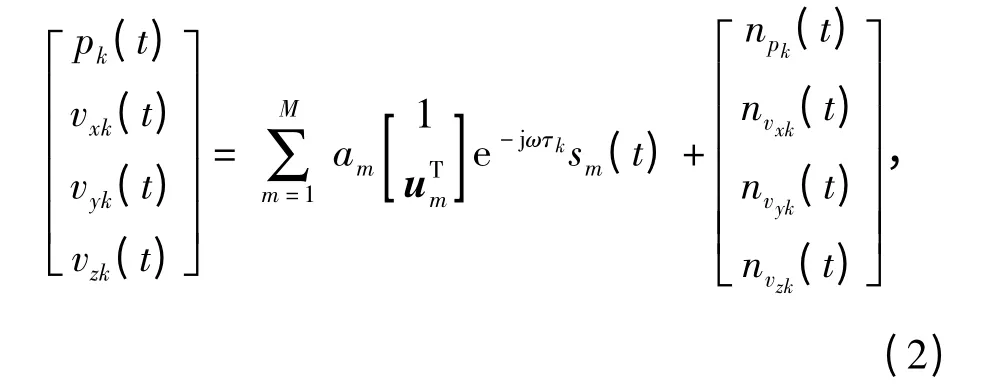
式中:am为第m 个信号源的振幅;ω 为信号角频率;sm(t)为第m 个信号源在参考点处的的声压复包络，且假设接收的噪声为均值为0 的高斯白噪声，各阵元间的噪声彼此不相关。

文中所采用的垂直矢量传感器阵列是以第一个基元为坐标原点，其他基元均匀分布在z 轴上的均匀线列阵，空间关系如图2所示。

假设阵元间距d，则延时τk=(k－1)dsin φm/c，并且令sm(t)均为ejωt，即M 个信号源相干，则阵列输出(2)式变为:

1.2 算法原理

本文以相干信号源为前提阐述垂直矢量阵CAATI 算法。

CAATI 算法的基础是prony 方法，理想情况下(假设噪声不存在)，prony 方法可以用零束控方程表示，对于声压传感器阵而言，M 个相干信号源的独立方程可以通过M 个长为M +1 的重叠子阵获得［1］，此时，阵元总数K =2M，存在复数加权ω 使得:

图2 垂直矢量阵空间关系示意图Fig.2 Space relation of a vertical vector sensor array

由(3)式可知，声压输出经离散化变为:

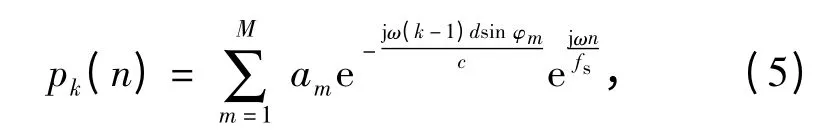
其中:z=exp(jωdsin φm/c)，显然方程组(6)每个方程的解均满足，因此只要得到ωm，即可得到z，从而解出信号源的俯仰角φm.

在实际情况中，由于噪声的存在使得(4)式不再成立，取而代之的是:

式中b 是噪声引起的扰动，此时可以利用总体最小二乘法［2］对(7)式进行求解，为了允许总体最小二乘法利用更多的接收数据信息，提高ω 的精确性，可以将P 写成如下形式:

计算出P 的奇异值，求得ω 的最小范数解，由于(3)式中设定ω0=1，因此解唯一。

当相干信号源的数目大于K/2 时，所获得的数据矩阵

式中:M ＞K/2，此时P'的秩小于M，故P'的行向量线性相关，即P'ω =0 并不满足独立方程的条件，因此，K 元声压阵最多可以同时获得K/2 个相干信号源的幅值和方位。

1.3 信号源数目估计方法

从(4)式可看出，一个K 元线阵可同时获得K/2 个相干信号源的信息。而实际情况中，信号源的数目并不知道。此时(4)式只能看作模型阶数为K/2的方程，也就是说虽然通过(4)式可以解出K/2个根，但实际信号源的数目可能小于K/2.这时可以利用门限法正确选择出信号源信息。

由(6)式可看出，理想情况下，当方程(4)式的根来自真正的信号源时，z 的模为1，因此在高信噪比的条件下可以设定一个很小的门限Δ，使得:

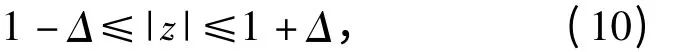
当z 满足不等式(10)时，认为所获得的结果正确，反之舍去。

门限Δ 的选取和信噪比大小以及经验密切相关，通常来讲，信噪比越高，门限Δ 越小;信噪比越低，门限Δ 越大;门限Δ 的取值在小范围变动时，对测量结果的影响并不大。

1.4 am 的求解方法

将(5)式写成矩阵形式有:

式中:S=［p1(n) p2(n) … pM(n)］T;

因此，

1.5 水平方位角θm 求解方法

由公式(3)可知，因为［1，uTm］T是一个实数矩阵，并不影响振速分量的结构，因此任何一个振速分量都可以用同样的方法解得目标幅值与俯仰角，显然目标的俯仰角是一致的，无需再次求解，不同的是幅值，由于相干信号的声压和振速应是同相或反相，而矢量传感器的声压和振速存在相位差，需要对其声压和振速进行相位校准，为了避免相位校准带来的工作量和误差，文中选择振速分量vxk(n)、vyk(n)求解目标的水平方位角。利用vxk(n)所得到的幅值为axm=cos φmcos θmam，利用vyk(n)所得到的幅值为aym=cos φmsin θmam，因此目标的水平方位角为:

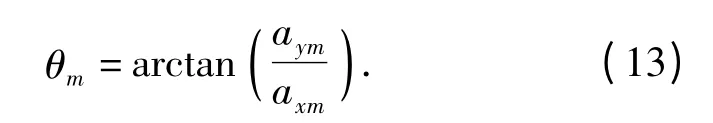
可见，将CAATI 算法应用到垂直矢量传感器阵上，无需二维结构即可实现目标空间方位估计。

根据实际情况的需要，布放的线列阵可能是垂直或水平的，故下面给出利用水平矢量阵实现CAATI 算法的推导结果，以供参考。

按照图2所示的空间关系，将CAATI 算法应用到水平矢量阵(沿x 轴布放)时，利用pk(t)所得到的角度不再是信号源的俯仰角φm，而是信号源的水平方位角θm，此时，可以利用振速分量vxk(n)和vzk(n)的幅值axm及azm求解俯仰角φm，经过推导，得到的结果如下:

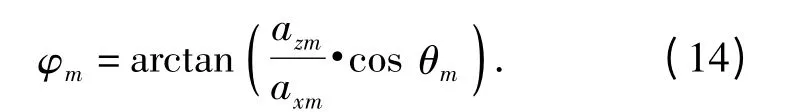
1.6 数据处理方法

由于噪声的存在可能会导致一次独立仿真实验的结果出现偏差，比如出现漏判或错判目标，尤其是在低信噪比时，一次仿真实验的结果会有很大偏差。文中进行100 次独立仿真实验，然后对比每次仿真实验的结果，按如下原则估计目标个数以及各个目标的正确方位。

1)在目标俯仰角的仿真结果中，如果大多数独立仿真实验结果满足不等式(10)的目标个数为Q，则认为实际的目标个数为Q.

2)舍弃目标个数不为Q 的独立仿真实验结果，在剩余的各次仿真实验结果中，舍弃有明显偏差的仿真结果。

3)将其余结果相加取均值，作为最后的目标俯仰角估计值。

4)选择与目标俯仰角仿真结果相对应的水平方位角估计结果，然后相加取均值，即为目标的水平方位角估计值。

2 仿真验证

2.1 相干点源的方位估计性能

考虑由6 个阵元组成的垂直矢量阵，信号频率f0=10 kHz，阵元间距d =λ/2，假定存在来自相同距离的2 个相干信号源(可被看作点源)，俯仰角分别为10°和－5°，水平方位角分别为15°和25°.利用垂直矢量阵CAATI 算法，选取模型阶数为3，快拍数为30，采用1.6 节的方法，对仿真数据进行处理，在不同信噪比时，得到的仿真结果如表1所示。

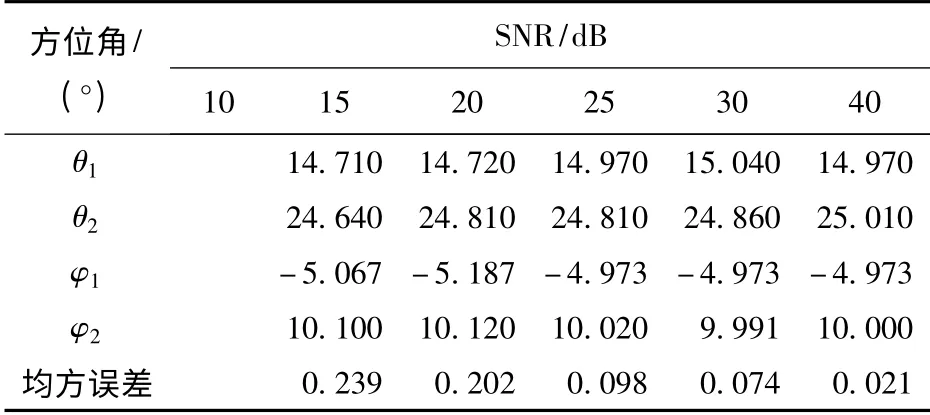
表1 不同信噪比时两个相干源的方位估计结果Tab.1 DOA estimations of two coherent signals in different SNR conditions

由表1可知，在信噪比低于15 dB 时，该算法已经失效，但当信噪比大于等于15 dB 时，该算法可以有效地实现目标的空间方位估计，并且随着信噪比的提高，方位估计性能也变得越来越好。

2.2 角度间隔对方位估计性能的影响

为了说明角度间隔对仿真结果的影响，仿真了信噪比为25 dB 时，两个相干信号源(可被看作点源)的水平方位角分别为15°和25°时，俯仰角的仿真结果随其角度间隔变化的平均误差(两信号源俯仰角的绝对误差的平均值)曲线，以及两个相干信号源的俯仰角分别为10°和－5°时，水平方位角的仿真结果随其角度间隔变化的平均误差曲线，如图3(a)～图(b)所示。

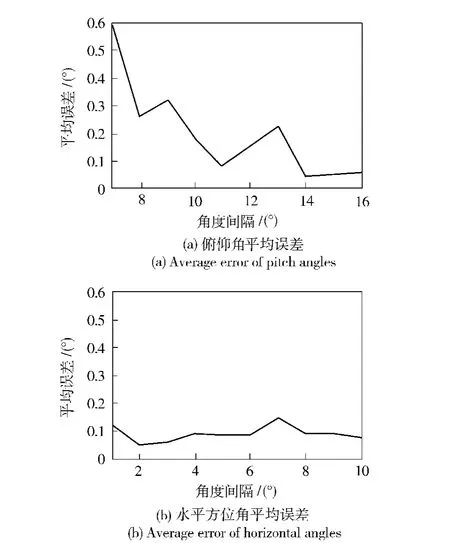
图3 角度间隔对仿真结果的影响Fig.3 Effect of angular spacing on simulation results

比较图3中(a)、(b)可以看出，在相干源的水平方位角良好区分的前提下，随俯仰角的角度间隔的增大，目标的俯仰角的平均误差基本呈减小趋势，即角度间隔越大，方位估计越精确，并且角分辨率仅为7°;而在相干源的俯仰角良好区分的前提下，水平方位角的角度间隔对仿真结果的影响并不大，并且水平方位角的角分辨率可以达到1°.这是由于水平方位角的获得仅是来自于振速分量vxk(n)、vyk(n)的代数运算，因而利用垂直矢量阵CAATI 算法在俯仰角良好区分的前提下可以获得更好的水平分辨率。

2.3 非点源目标的方位估计性能

本小节给出利用6 阵元垂直矢量阵对空间非点源(可看成由有限点源组成)目标进行空间方位估计的仿真结果(距离可由主动测距法获得，仿真中假设距离已知)，为了验证矢量阵CAATI 算法对同一距离相干源的方位估计性能，构造如图4所示的仿真模型。图5(a)为信噪比趋于无穷大时，对图4所示目标的仿真结果;图5(b)为信噪比为25 dB 条件下的仿真结果。

从图5(a)可看出，没有噪声时，仿真结果与构造的目标模型一致，可以准确的实现目标方位估计;而图5(b)在相同的条件下增加了高斯白噪声(SNR=25 dB)，噪声的加入影响了算法的角度分辨率，因此在同一距离的两个点源角度间隔较小时，算法无法分辨出它们，取而代之的是两个角度的均值(0°左右)，所以得到图5(b)所示的仿真结果。

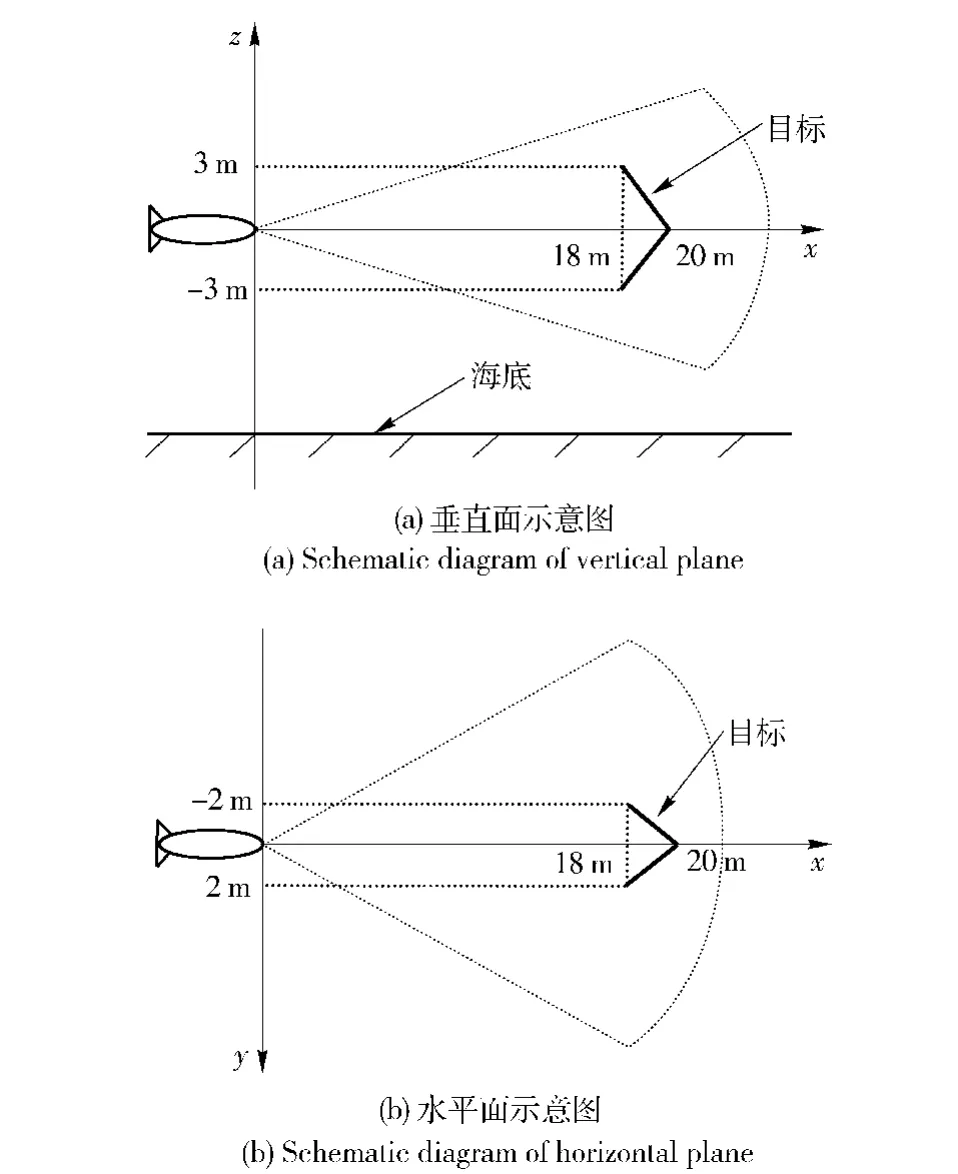
图4 目标模型几何关系示意图Fig.4 Schematic diagrams of simulated target geometry

3 结论

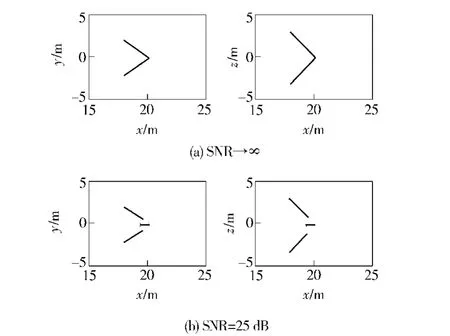
图5 不同信噪比下目标仿真结果Fig.5 Simulation results of simulated target in different SNR conditions

本文将CAATI 算法引入到矢量阵目标方位估计处理中，研究了远场条件下，基于垂直矢量线列阵CAATI 算法的测向性能。给出了仿真结果，说明矢量CAATI 算法可以有效地实现目标空间方位估计，并且在相干源的俯仰角良好区分的前提下，仅需6个基元就能达到1°的水平方位角分辨率，有效地提高了方位估计的性能。

References)

［1］ Kraeutner P H，Bird J S.Principal components array processing for swath acoustic mapping［J］.IEEE Proceedings of OCEANS’97 MTS，1997，(2):1246－1254.

［2］ 张贤达.现代信号处理［M］.北京:清华大学出版社，1995.ZHANG Xian－da.Modern signal processing［M］.Beijing:Tsinghua University Press，1995.(in Chinese)

［3］ Kraeutner P H，Bird J S.Beyond interferometry，resolving multiple angles－of－arrival in swath bathymetric imaging［J］.IEEE Proceedings of Riding the Crest into the 21st Century of OCEANS’99 MTS，1999，(4):37－45.

［4］ Kraeutner P H，Bill C.Multiangle swath bathymetry sidescan quantitative performance analysis［J］.IEEE of OCEANS’02 MTS，2002，(4):2253－2263.

［5］ 李海森，黎子盛，周天，等.MSB－CAATI 算法在多波束测深系统中的应用［J］.声学技术，2007，26(2):286－290.LI Hai－sen，LI Zi－sheng，ZHOU Tian，et al.Application of MSBCAATI algorithm to multi－beam bathymetry system［J］.Technical Acoustics，2007，26(2):286－290.(in Chinese)

［6］ Song Hai－yan，Piao Sheng－chun.A new method for DOA and amplitude joint estimation［C］∥Industrial Electronics and Applications of ICIEA.Xi’an:ICIEA，2009，1097－1102.

［7］ Wen Xu，Kraeutner P，Guo H，et al.First results of a novel and low power forward looking sonar technology for small AUV’s［J］.IEEE of Oceans，2006，(1):1－3.

［8］ 孙贵青，李启虎.声矢量传感器信号处理［J］.声学学报，2004，29(6):491－498.SUN Gui－qing，LI Qi－hu.Acoustic vector sensor signal processing［J］.Acta Acustica，2004，29(6):491－498.(in Chinese)

［9］ 黎子盛，张建华，周天，等.基于L 型阵列的二维CAATI 算法高分辨DOA 估计［J］.海洋测绘，2007，27(1):27－29.LI Zi－sheng，ZHANG Jian－hua，ZHOU Tian，et al.Two－dimensional CAATI algorithm for high resolution DOA estimation based on L－shaped array［J］.Hydrographic Surveying and Charting，2007，27(1):27－29.(in Chinese)

［10］ 周浩，蒋兴舟.基于矢量传感器阵列的二维波达方向估计研究［J］.武汉理工大学学报，2007，31(2):220－223.ZHOU Hao，JIANG Xing－zhou.Study of the two－dimension DOA estimation technology based on the acoustic vector array［J］.Journal of Wuhan University of Technology，2007，31(2):220－223.(in Chinese)

［11］ 王永良.空间谱估计理论与算法［M］.北京:清华大学出版社，2004.WANG Yong－liang.Spatial spectrum estimation theory and algorithm［M］.Beijing:Tsinghua University Press，2004.(in Chinese)