近场水下爆炸作用下箱形梁整体损伤特性研究

李海涛，张永坤，张振海

(1.海军工程大学 科研部，湖北 武汉430033;2.海军91439 部队，辽宁 大连116041)

0 引言

现代海战中，舰船遭受的水下爆炸攻击多以近场作用为主。舰船的细长结构形式决定了其固有频率多在几个赫兹范围内，这与常规水中兵器爆炸形成的气泡脉动频率吻合，爆炸气泡与舰船之间的耦合激励作用更容易被激发出来。研究舰船在近距水下爆炸作用下的整体响应特点及损伤模式，对于水中兵器设计及舰船结构防护均具有重要意义。

关于水面整体结构在水下爆炸作用下的响应研究，已有工作主要集中于中远距离爆炸［1－3］。近年来，随着人们对水下爆炸载荷认识的加深，近距爆炸载荷作用下舰船整体响应研究逐步增多。如文献［4］对船体梁模型在中部近场爆炸气泡作用下的动态响应特性进行了研究，发现气泡收缩过程中船体梁处于中垂应力状态，最后对中垂弯曲载荷的形成原因进行了分析。文献［5］利用有限元和边界元相结合的方法对气泡近场作用下舰船整体运动响应情况进行了模拟，发现气泡脉动期间，舰船整体出现中垂变形，但并未对破坏机理进行深入分析，也未给出中垂破坏的条件。

本文利用试验和数值仿真相结合的方法，对箱形梁模型在水下近距非接触爆炸作用下的整体响应特性进行研究。分析了爆炸气泡激起梁低阶运动时，梁的总体响应特点及损伤模式，初步给出了中垂损伤条件，并简要分析了损伤机理。

1 箱形梁模型设计

以某型舰为母型(具体参数略)，设计了一种简化的船体梁模型。鉴于试验条件限制，在准确相似的缩比模型基础上，以总纵强度相似为原则，对原模型进行简化，采用能表征典型水面结构整体形式的箱形梁模型作为研究对象。

设计船体梁模型时，将原型主要构件质量计入船体板质量，试验模型不设置纵、横向加强构件;忽略原型舰船设备布置对质量分布的影响，试验模型中不另行配重。如图1所示，给出了箱形梁模型的具体结构形式及主要尺寸，模型板厚均为3 mm，总质量34.2 kg，材料采用Q235A 钢，模型弹性极限弯矩2.29 ×104N·m.利用有限元软件Abaqus 实体建模，计算得到箱形梁模型的一阶理论湿模态频率为24.8 Hz，试验测得其一阶湿模态频率为21.4 Hz.

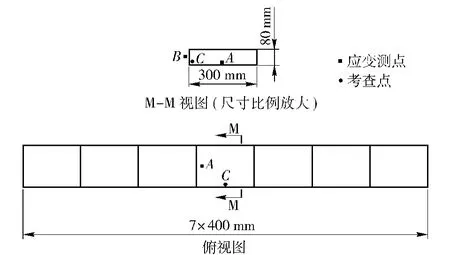
图1 梁结构尺寸及测点布置Fig.1 Structure of beam and position of sensors

2 数值仿真方法

2.1 计算模型

箱形梁在水下近距爆炸作用下整体响应的数值研究主要基于通用有限元分析软件MSC.Dytran 进行。如图2所示，给出了整个数值计算模型。利用四边形壳单元建立梁结构，梁模型上部的空气域高0.5 m，下部水域深2.5 m，空气域设为流入流出边界，水域四周设为封闭边界。欧拉流场和拉格朗日结构之间采用一般耦合方式。将TNT 炸药置于箱形梁中部正下方爆炸。在近自由水面条件下，5 g TNT 药量形成的气泡脉动频率约20 Hz，与计算模型的一阶湿频率相近，因此本文将其作为分析药量值，并选取0.3 m、0.5 m、1.0 m 三种爆距进行相关仿真及试验研究。

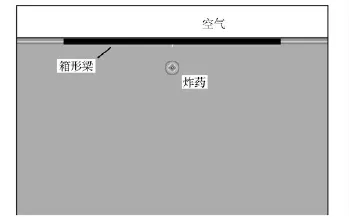
图2 数值计算模型Fig.2 Numerical analysis model

计算时考虑重力因素及弹性板的应变率强化效应。弹性板材料使用低碳钢，弹性模量为210 GPa，泊松比为0.3，密度为7 800 kg/m3，静态屈服极限为250 MPa，设置最大塑性应变为0.25.计算中应变率强化模型采用Cowper－Symonds 模型［6］:

式中:σd、σy分别为动态、静态屈服极限为等效应变率;D、P 为应变率强化参数，对低碳钢，一般取D=40，P=5.

2.2 状态方程

状态方程用来定义固体和流体在各种不同状态下的压力、密度以及比内能之间的函数关系，正确选取状态方程中的参数对于计算结果至关重要。水和理想气体状态方程的参数设置如下所述。

对于中等强度爆炸冲击波，通过介质后熵值变化很小，接近于等熵过程［7］，此时水介质的状态方程可表示为

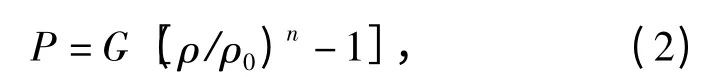
式中:G=2.98 ×108Pa;n=7.15.

将水的状态方程［8］以多项式的形式进一步表示如下:

式中:μ=(ρ/ρ0)－1;ρ0=1 000 kg/m3，为常温下水的密度;ef=83 950 J/kg，为水的质量比内能;a1=2.2 ×109;a2=9.54 ×109;a3=1.457 ×1010;b0=0.28;b1=0.28.

假定水下爆炸气泡运动过程为等熵膨胀过程，可采用理想气体状态方程［8］:

式中:ρg为气体密度;eg为气体质量比内能，爆炸气体取4.19 ×106J/kg;γ 为气体比热比，TNT 炸药爆炸气体取1.25.

2.3 爆炸载荷处理方法

水中炸药在爆轰瞬间，形成高温、高压、高密度的爆炸气团。假设炸药在化学爆轰过程中没有质量损失，即认为初始爆炸气团质量与炸药质量相等，此时就可将瞬态爆炸炸药作为高压气团处理，并忽略气团与周围水介质的热传递过程，认为其为等熵膨胀过程，按理想气体处理［6］。这样就可通过建立气、液多欧拉流体单元，来模拟水下爆炸气泡的运动过程。该处理方法解决了JWL 方程对气泡模拟的不足，能较好地模拟后续气泡脉动过程。爆炸气泡的初始半径可参考文献［9］的方法计算求得。经计算，在本文选取的爆深条件下，5 g TNT 炸药爆炸的初始气泡半径约为7.8 cm，本文将以该值作为高压气团的初始半径值。

由于流体静压力对水下爆炸气泡的动力学特性影响较大，因此必须在数值模拟中设定静压场，才能较好地模拟水下爆炸气泡的动力学过程。“Exflow2”子程序可根据不同水深条件和边界条件对流域边界施加静压场。由于本文计算水域较小，压力在深度方向变化不大，遂采用全局加载相同外部压力的近似方法处理流体初始压力问题。

2.4 网格尺寸选取

总结已有数值仿真经验发现，流体网格尺寸大小对计算精度的影响较大，流体网格偏大或偏小，都可能造成计算结果误差增大。为了合理确定计算模型的流体网格尺寸，本文选取一系列流体单元尺度进行计算，通过将计算值和经验值进行比较，获得较为合理的流体网格尺度。设气泡初始半径为r0，流体单元最大边长L，参数E 表征气泡最大半径的计算值与经验值之间的绝对误差。如图3所示，给出了绝对误差E 随比值L/ r0变化的关系曲线。

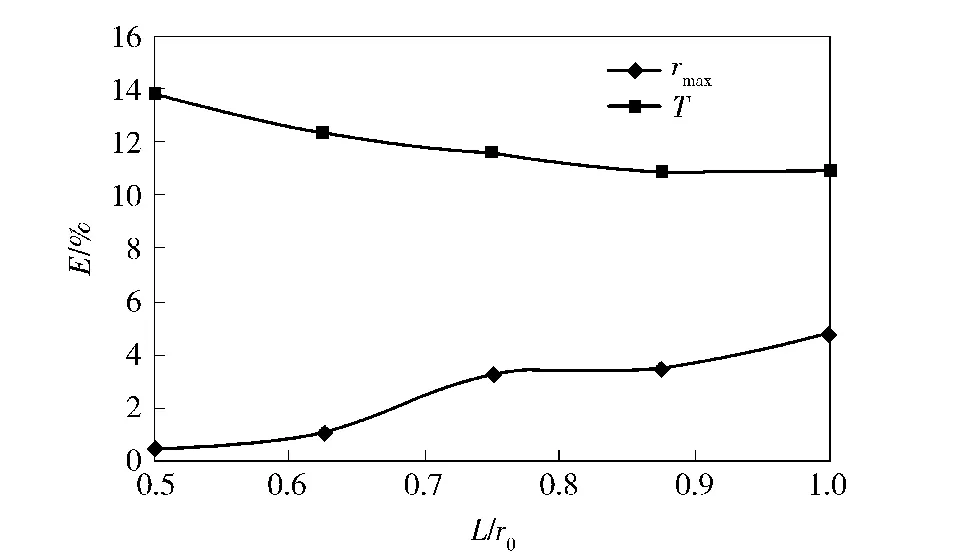
图3 网格尺寸对气泡计算参数的影响Fig.3 Effects of mesh sizes on bubble’s parameters

从图3可看出，随着比值L/r0的增大，最大气泡半径rmax和气泡脉动周期T 的计算误差呈相反的变化规律。随着网格尺寸的增加，气泡最大半径的误差逐渐增大，而气泡脉动周期的误差逐步减小。综合考虑网格尺寸对两种参数的影响，本文将比值L/r0=0.625 作为流体网格尺寸选取参考值。

3 结果及分析

本文针对数值仿真工况对箱形梁模型进行水下爆炸试验，并利用高速摄影仪观测整个水下爆炸过程，最后结合数值仿真结果和试验结果综合分析箱形梁在水下近距爆炸条件下的整体运动响应特性。

水下爆炸试验中设置了两个自由场压力传感器P1、P2，用来测量冲击波和气泡脉动压力参数。如表1所示，给出了3 种爆炸工况下，通过分析P1，P2压力传感器的压力参数得到的冲击波和气泡脉动压力的冲量值。可看出，不同爆深工况下，爆炸冲击波和气泡脉动压力形成的冲量值基本相当。

3.1 总体响应特性

不同爆距条件下，箱形梁模型表现出不同的响应特点:0.3 m 爆距时，结构发生明显的中垂弯曲变形，同时舷侧结构出现褶皱屈服;0.5 m 爆距下，梁整体中垂变形较小，但中部舷侧结构出现褶皱屈服;当爆距为1.0 m 时，结构处于弹性响应阶段，表现出明显的鞭状运动过程。

以0.3 m 爆距工况为例，具体分析箱形梁的整体运动响应过程。整个过程利用高速摄影仪记录，拍摄频率250 帧/s.该工况下，在气泡膨胀的初始阶段，箱形梁中部存在明显的高应力区，但尚未出现整体结构变形;随着气泡的膨胀，箱形梁发生一定的中拱弯曲变形，约15 ms 时，梁中部的弹性运动位移达到3.5 cm，此时梁的舷侧部分存在较大的结构应力;当气泡膨胀到最大后，梁结构会随着气泡的收缩过程而回复到水平状态并进一步向中垂状态变化;约30 ms 时，梁整体结构已出现一定的中垂弯曲变形，结构舷侧部分存在高应力区，并出现褶皱变形;随着气泡的收缩，梁中垂弯曲变形逐步增大，其中部出现了一个固定塑性绞，梁两端绕着塑性铰发生相对转动;当气泡收缩到最小时，中垂变形达到最大值，其中试验值为13.2 cm，计算值12.6 cm，相对误差4.5%.如图4所示，给出了气泡膨胀和收缩溃灭阶段，箱形梁弯曲变形的数值仿真和试验结果比较。

表1 不同爆深条件下冲击波和气泡脉动压力冲量值Tab.1 Impulsions of shockwaves and bubble oscillations in tests

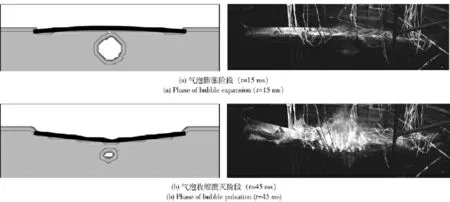
图4 近距气泡作用下箱形梁变形过程的试验(右)及仿真结果(左)比较Fig.4 Comparison between numerical and experimental results about beam deformation subjected to explosion bubble

3.2 结构应变响应特性

为具体分析不同工况下箱形梁结构的应变响应特性，选取应变点A、B 为分析对象，其中A 点布置于梁中部底板，B 点置于中部舷侧壁，主要考察结构的整体纵向变形。考察点具体位置如图1所示。如表2所示，给出了各工况下两个测点应变峰值的试验值和计算值比较情况，表中参数R、rmax分别表征爆距及气泡最大半径。由比较数据可以看出:计算得到的冲击波和气泡脉动压力引起的应变峰值与试验值吻合较好，误差基本在10%以内;气泡脉动压力形成的结构应变响应大于冲击波形成的应变响应，而由表1中的数据可知两者形成的冲量相当，可见箱形梁与气泡的耦合激励作用对整体结构的损伤作用明显，这种耦合激励进一步强化了水下爆炸载荷对整体结构的冲击效果;随着爆径比的增大，测点应变峰值随之减小，且减小幅度呈非线性变化趋势。在0.3 m、0.5 m 爆距条件下，舷侧结构出现屈服破坏，B 点所得试验数据不可靠，故舍去。

如图5所示，给出了0.5 m 爆距条件下，A、B 测点应变时程曲线的试验值和计算值比较。可以看出，计算结果与试验结果吻合较好，两条曲线呈现出相同的变化规律;由A 点的应变曲线可以看出，在气泡脉动中期，测点基本处于中垂应变状态，且持续时间较长，维持了约25 ms 的时间;B 点在约15 ms时刻开始进入中垂应变状态，约23 ms 时刻，中垂弯曲过程开始加速，此时也正是气泡进入快速收缩的时刻;约30 ms 时，测点进入塑性屈服阶段，舷侧结构出现褶皱破坏。可见，该爆距条件下，爆炸气泡对结构的中垂损伤作用仍比较明显。

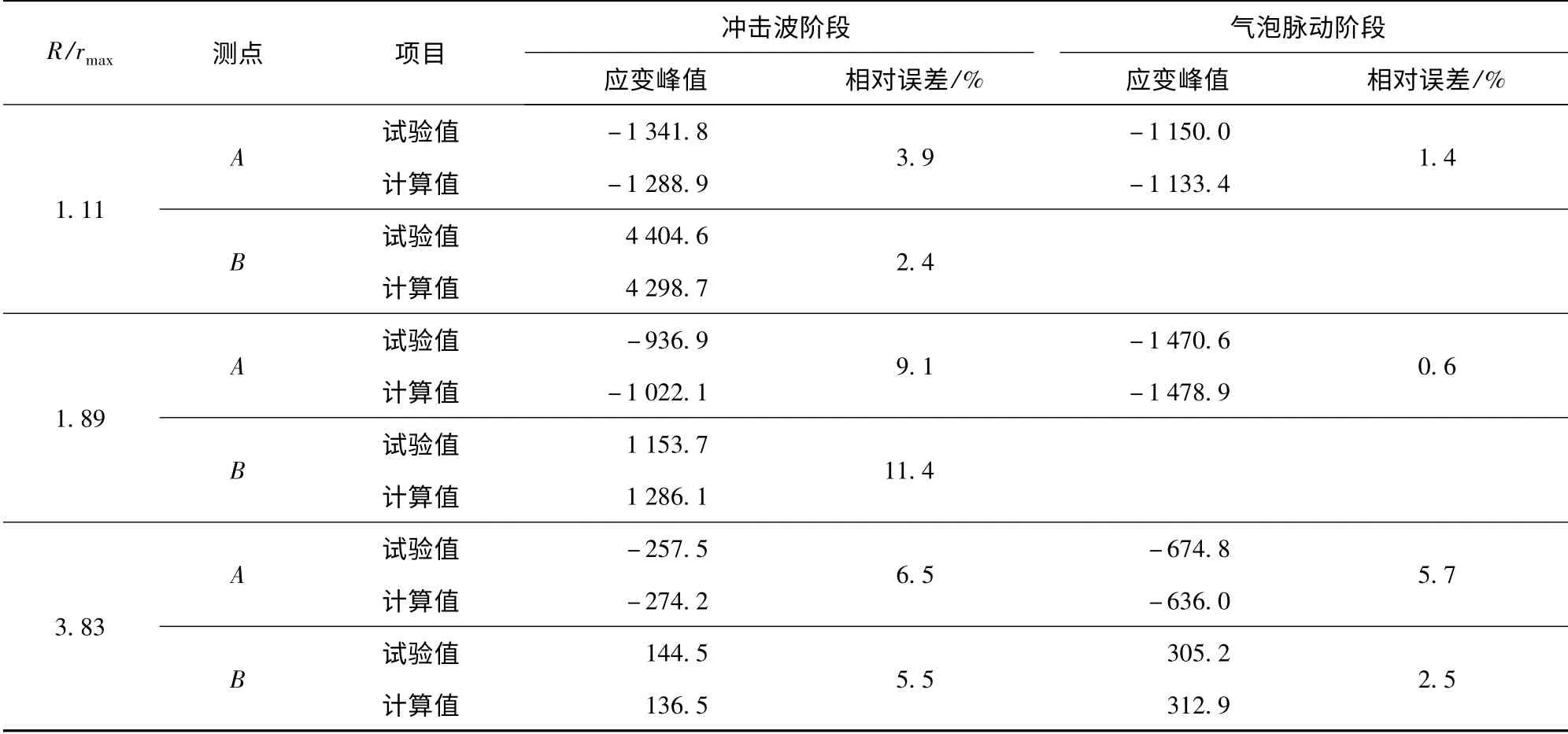
表2 结构应变的计算及试验结果对比Tab.2 Comparison between numerical results and experimental results of strains

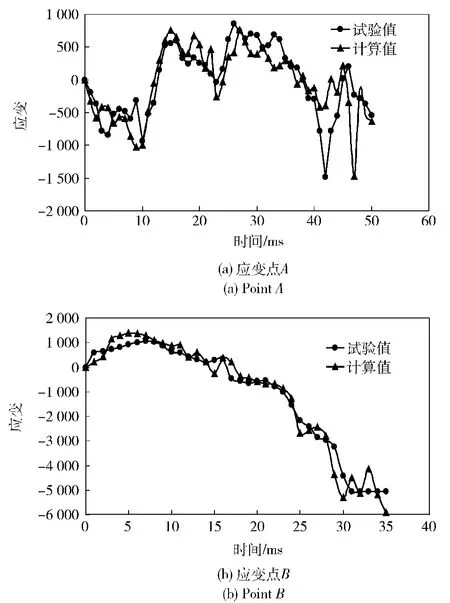
图5 典型应变测点的试验值和计算值比较(R=0.5 m)Fig.5 Comparison between numerical and experimental results about strains on model (R=0.5 m)

由以上数据分析可以看出，相同药量条件下，爆距越小，气泡运动对造成梁结构整体塑性变形的作用越大。在0.3 m 爆距条件下，结构整体响应明显，呈现先中拱弯曲，后中垂弯曲破坏的响应特点，该响应模式值得深入分析。以箱形梁中部且靠近舷侧隔板的测点C 为研究对象(具体位置参见图1)，分析0.3 m 爆距条件下整体结构的应变响应特点。该点的具体应变曲线如图6所示。

图6 箱形梁C 点应变时程曲线(R=0.3 m)Fig.6 Curve of strain at point C (R=0.3 m)

由图6可以看出:气泡膨胀初期，结构受初始冲击波作用，C 点快速出现压应变峰值;随着气泡的进一步膨胀，测点仍处于压应变状态，结构在气泡作用下保持明显的中拱弯曲变形;约20 ms 时刻，气泡进入膨胀后期，结构应变值快速减小，并逐步向拉应变状态转化，说明此时结构受到中垂弯矩作用;约30 ms时刻，气泡开始快速收缩，C 点进入拉应变状态，随着气泡的继续收缩，该状态保持不变，说明此时梁结构已经发生中垂弯曲变形。如图7所示，给出了0.3 m 爆炸工况下，通过试验获得的梁最终损伤变形情况，可见其发生明显的中垂弯曲破坏。

图7 箱型梁中垂损伤情况(R=0.3 m)Fig.7 Sagging damage mode of beam (R=0.3 m)

在0.3 m 爆炸条件下，气泡快速收缩使梁结构由中拱变形转化为中垂弯曲变形，说明气泡收缩使结构受到明显的中垂弯矩作用，该作用来自于箱形梁底部流场压力的降低，而这种流场压力的变化正是近距脉动气泡引起的;当整体结构和气泡发生耦合运动时，耦合激励会进一步增大中垂弯曲效果。在中远场爆炸条件下，气泡脉动对梁底部流场压力的影响减小，形成的中垂弯曲效果不明显，此时结构和气泡的耦合运动仅激起鞭状运动响应，而整体结构仍处于弹性变形过程。

4 结论

为研究舰船在近距爆炸作用下的运动响应及损伤模式，设计了一种箱形梁模型，利用试验和数值仿真方法对该模型在近距非接触爆炸作用下的整体运动响应特性进行了研究，得出主要结论如下:

1)所建立的数值仿真方法对于模拟近距水下爆炸作用下箱形梁结构的动态响应过程具有较好的精度，能够预报结构模型的应变响应过程及最终塑性变形，计算误差基本控制在10%以内。

2)当爆炸气泡脉动频率与结构一阶频率相近时，梁结构在受到中垂弯矩作用的同时，还会受到气泡的耦合激励作用，两种效果的叠加导致梁结构发生整体中垂破坏，出现固定塑性绞。

3)耦合运动条件下，爆径比越小，对结构的整体损伤作用越大;随着爆径比的进一步增大，梁结构主要变现为鞭状运动响应。

References)

［1］ Li Y J，Pan J Q，Li G H，et al.Experimental study of ship whipping induced by underwater explosive bubble［J］.Journal of Ship Mechanics，2001，5(6):75－83.

［2］ Shin Y S.Ship shock modeling and simulation for far－field underwater explosion［J］.Computers and Structures，2004，82(23－26):2211－2219.

［3］ Zong Z.A hydroplastic analysis of a free－free beam floating on water subjected to an underwater bubble［J］.Journal of Fluids and Structures，2005，20(3):359－372.

［4］ 李海涛，朱锡，黄晓明，等.近场脉动气泡作用下船体梁模型动响应试验研究［J］.哈尔滨工程大学学报，2008，29(8):773－778.LI Hai－tao，ZHU Xi，HUANG Xiao－ming，et al.An experimental study on the dynamic response of ship－like model subjected to underwater explosion bubble located closely［J］.Journal of Harbin Engineering University，2008，29(8):773－778.(in Chinese)

［5］ 张阿漫，姚熊亮.水下爆炸气泡与复杂弹塑性结构的相互作用研究［J］.应用数学和力学，2008，29(1):81－92.ZHANG A－man，YAO Xiong－liang.Interaction of underwater explosion bubble with complex elastic－plastic structure［J］.Applied Mathematics and Mechaincs，2008，29(1):81－ 92.(in Chinese)

［6］ 李海涛，朱锡，张振华，等.弹塑性边界下水下爆炸气泡动态特性的数值仿真研究［J］.系统仿真学报，2009，21(14):4532－4535.LI Hai－tao，ZHU Xi，ZHANG Zhen－hua，et al.Numerical simulation study of pulsation dynamics of underwater explosion bubble located under elastoplastic plane［J］.Journal of System Simulation，2009，21(14):4532－4535.(in Chinese)

［7］ 张振华，朱锡，白雪飞.水下爆炸冲击波的数值模拟研究［J］.爆炸与冲击，2004，24(2):182－188.ZHANG Zhen－hua，ZHU Xi，BAI Xue－fei.The study on numerical simulation of underwater blast wave［J］.Explosion and Shock Waves，2004，24(2):182－188.(in Chinese)

［8］ 宗智，邹丽，刘谋斌，等.模拟二维水下爆炸问题的光滑粒子(SPH)方法［J］.水动力学研究与进展:A 辑，2007，22(1):61－67.ZONG Zhi，ZOU Li，LIU Mou－bin，et al.SPH simulation of twodimensional underwater explosion［J］.Journal of Hydrodynamics:Ser.A，2007，22(1):61－67.(in Chinese)

［9］ Klaseboer E，Khoo B C，Hung K C.Dynamics of an oscillating bubble near a floating structure［J］.Journal of Fluids and Structures，2005，21(4):395－412.