径向浮环动静压轴承稳定性研究

郭 红，张直明，岑少起，陈昌婷

（1.郑州大学 机械工程学院，郑州 450001；2.上海大学 机电工程与自动化学院，上海 200072）

动静压浮环轴承具有摩擦功耗低、精度高、寿命长、稳定性好等突出优点，在航空航天、空分及精密加工机床等高速、超高速旋转机械上广泛应用［1-3］。国内外很多学者对不同工况下的动静压轴承进行了大量研究，尤其是在非线性领域［4-6］和高速运转时稳定性方面［7-9］。对于浮环轴承，康召辉等［10］研究了浮环涡动特性，得到了稳态时浮环质心运动轨迹为椭圆形的结论；郭红等［11］采用将浮环轴承内外两层油膜刚度系数和阻尼系数进行串并联的方法进行建模，对不同转速和偏心率下浮环动静压轴承的稳定性进行了仿真和试验。本文考虑浮环轴承内外层油膜之间的相互作用，针对轴颈和浮环分别建立动力学方程，得到系统完整的动力学模型。在有限元仿真的基础上，给出了径向浮环轴承的稳定性判据，并计算了特定结构参数轴承在不同偏心率下的失稳转速。为高速浮环轴承的稳定性建模和计算分析提供了一定的理论基础。

1 径向浮环轴承控制方程

图1为径向浮环轴承结构示意图，轴颈和浮环之间形成内膜，浮环和轴瓦之间形成外膜。内膜采用四腔结构，外膜采用五腔结构，内外膜每个腔都设置有深腔和浅腔。深腔具有静压效应，浅腔和封油边具有动压效应。

图1 向心浮环轴承结构Fig.1 Journal floating ring hybrid bearing

1.1 控制方程

取无量纲因子如下，并用Φ表示圆周方向坐标，λ表示轴向方向坐标，可得到内外膜无量纲动态Reynolds方程：

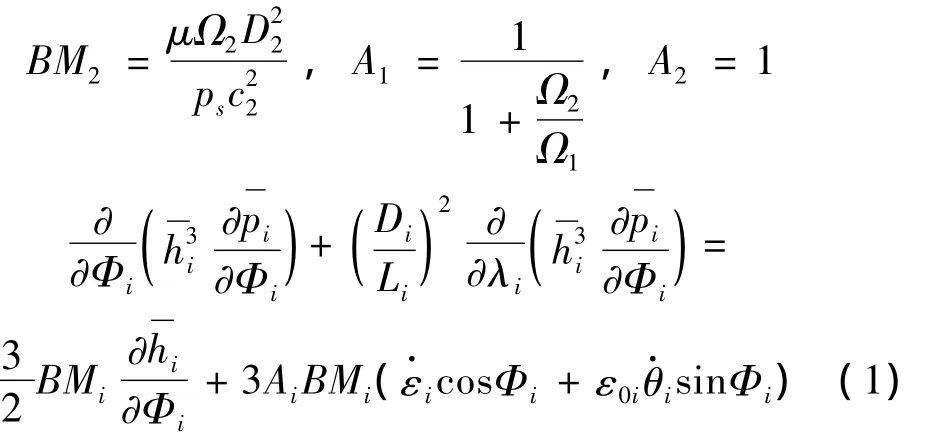
1.2 边界条件

如图2所示，向心浮环内外膜满足如下压力边界条件和深腔节流器流量平衡条件。

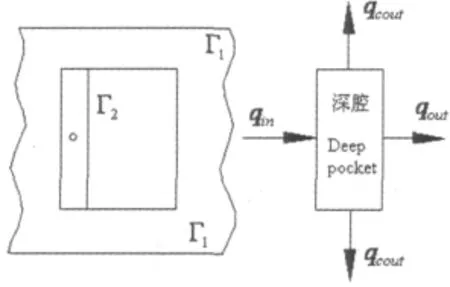
图2 压力边界条件及流量平衡条件Fig.2 Pressure boundary condition and restrictor flow equation

压力边界条件为：

无量纲深腔流量平衡方程为：

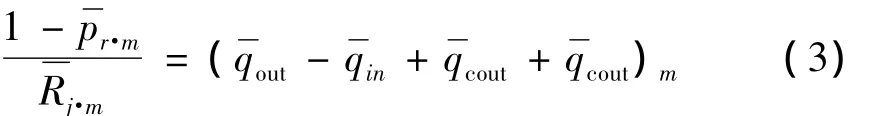
1.3 油膜厚度

内外膜无量纲油膜厚度可表示为：

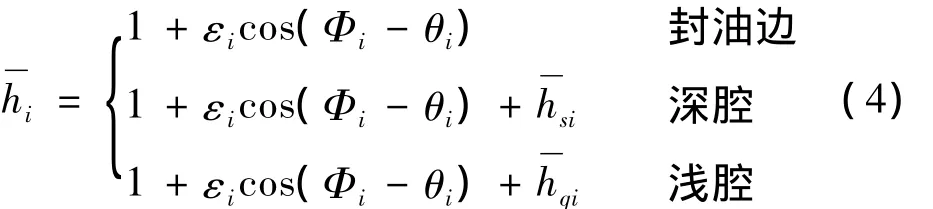
1.4 浮环平衡工作条件

满足内外膜作用到浮环的力和力矩平衡条件时，浮环即可以一定的转速平衡运转。

式中：Di为轴承直径（mm）；Li为轴承长度（mm）；hi为油膜厚度（mm）；ci为油膜间隙（mm）；Ω为轴颈角速度（1/s）；Ω2为浮环角速度（1/s）；ei为偏心距（mm）；hsi为深腔厚度（mm）；hqi为浅腔厚度（mm）；ε0为静平衡位置偏心率；θi为偏位角；μ为润滑油粘度（Pa·s）；pi为油膜压力（Pa）；psi为供油压力（Pa）；Fri为内外膜作用到浮环的力（N）；Mri为内外膜作用到浮环的力矩（N·mm）；kmni，（m，n=x，y）（N·mm-1）为刚度系数；bmni，（m，n=x，y）（N·s·mm-1）为阻尼系数。

下标i=1表示内膜参数，下标i=2表示外膜参数；带上划线者为无量纲参数，其余为有量纲参数。其他未标注者同一般润滑理论规范。

2 向心浮环轴承稳定性分析

浮环轴承内外膜动力学模型如图3所示，设轴颈质量为2mR，不计浮环质量。内层油膜的动力特性系数为kxx1，kxy1，kyx1，kyy1，bxx1，bxy1，byx1，byy1；外层油膜的动力特性系数为kxx2，kxy2，kyx2，kyy2，bxx2，bxy2，byx2，byy2。作用在轴颈上的简谐变动力为Fx，Fy；轴颈的简谐变动位移x1，y1；浮环的简谐变动位移x2，y2。

轴颈运动方程为：

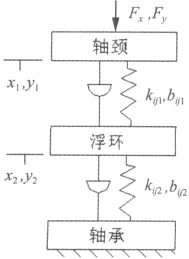
图3 浮环轴承内外膜动力学模型Fig.3 Dynamics model of floating ring bearing

浮环运动方程为：

式（7）式（8）解的一般形式可表示为：x1=x10evt，y1=y10evt，x2=x20evt，y2=y20evt，式中下标 0 表示振幅，v为复数，代入式（7）、式（8）得到：

式中：

式（10）非平凡解存在条件为系数矩阵的行列式等于零，将式（10）的行列式展开，得到特征方程为：

其中：

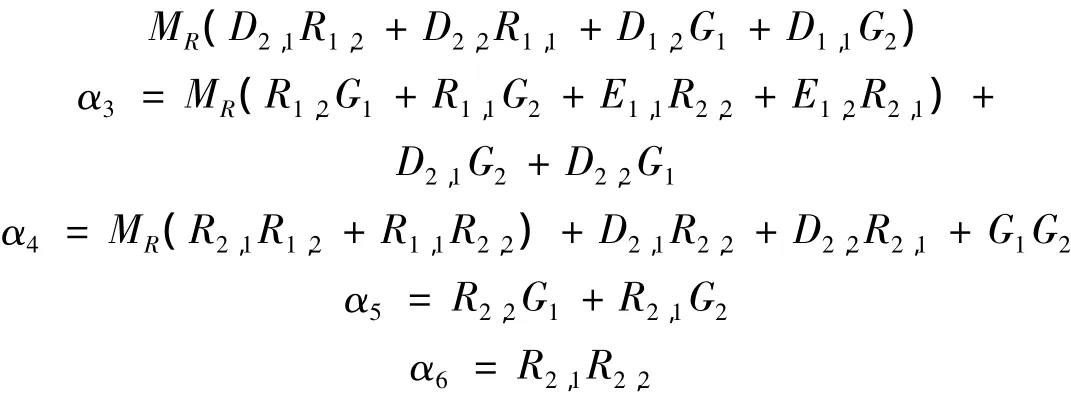
其中：

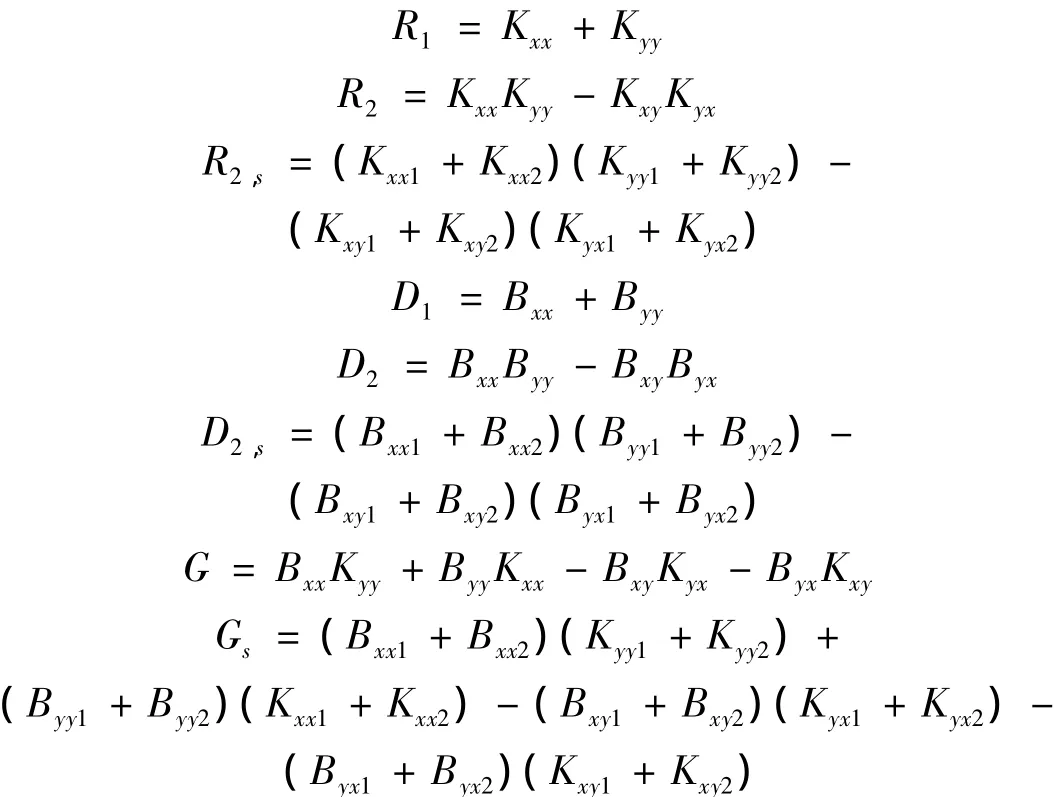
对于径向浮环动静压轴承，n=6，由Routh-Hurwitz准则，当α0＞0时，油膜涡动为稳定的充要条件是：

即可得到径向浮环动静压轴承稳定性判别条件：

因此，只要求出了浮环轴承内外膜的无量纲刚度系数和阻尼系数，即可按照上述稳定性条件判断浮环轴承是否处于稳定状态。

除了按照判别条件式（13）进行稳定性判断之外，还可以计算浮环轴承的失稳转速。特征方程（11）有三对根，它们为共轭复根。三对根数实部负值越大，油膜越稳定。在临界状态下，根的实部为零。对于工况条件和结构参数一定的浮环动静压轴承，刚度系数和阻尼系数与转速及偏心率有关，某一特定的转速对应一自由振动的运动方程。计算时可采用迭代法，在选定偏心率下求出方程的三对复数解，如果解的实部全为负，则轴承—转子系统是稳定的，以一定的步长增加系统的转速，直到解的实部变为零，则此转速即为系统选定偏心率下的失稳转速。

3 向心浮环轴承稳定性分析算例

表1为图1向心浮环动静压轴承结构参数。

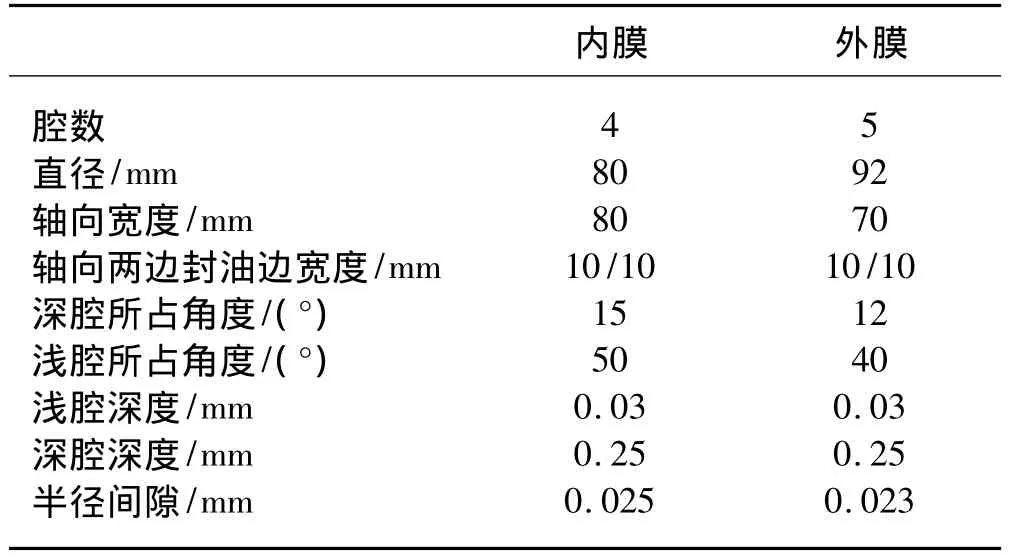
表1 向心浮环轴承结构参数Tab.1 Bearing Operating and Geometric Parameters

取润滑油粘度μ=4.475×10-3Pa·s，供油压力ps=1 MPa，经有限元计算后可得到该轴承压力分布、静特性参数和刚度阻尼等动特性参数。

图4为轴颈转速10 000 r/min时内外膜在偏心率0.15下的压力分布。由图中可以明显看出，内膜四腔出现四个压力峰值，外膜五腔呈现五个压力峰值，动压效应明显；深腔部分腔压稳定，为静压效应。

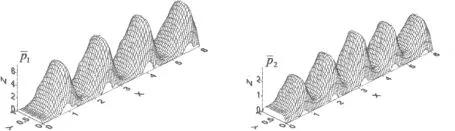
图4 内外膜压力分布（10 000 r/min，ε=0.15）Fig.4 Inner and outer film pressure distribution

图5～图8为不同转速下内外膜部分无量纲刚度系数和阻尼系数随偏心率变化曲线，对于动静压轴承来说，无量纲动态特性参数在不同转速和不同偏心率下都是不同的，正确求解这些系数是浮环轴承稳定性分析的前提。

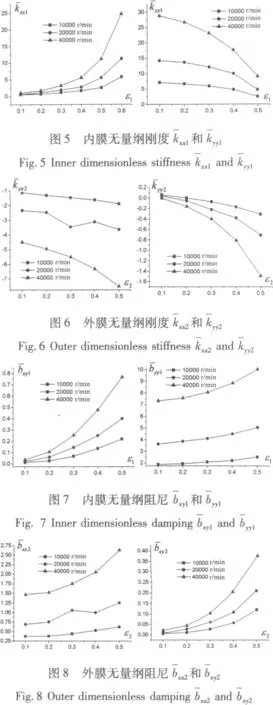
在刚度系数和阻尼系数计算的基础上，可以得到该浮环轴承不同偏心率下的失稳转速，如表2所示。可以看出，浮环轴承稳定性极佳，且随着偏心率的增加，失稳转速上升很快。因此高速时可以采取减小长径比、降低供油压力等措施来增大浮环轴承工作的偏心率，从而提高其失稳转速。

表2 浮环轴承失稳转速Tab.2 Threshold speed of journal floating ring hybrid bearing

4 结论

（1）考虑浮环轴承内外两层油膜的相互作用，针对轴颈和浮环建立系统统一的动力学方程，在此基础上给出了径向浮环动静压轴承的稳定性判据。

（2）对特定结构参数的径向浮环动静压轴承进行了有限元计算，得到了不同转速下刚度系数和阻尼系数随偏心率变化的曲线。在此基础上，计算了不同偏心率下轴承的失稳转速，且浮环轴承失稳转速随着偏心率的增加而迅速提高。

（3）增加浮环轴承工作的偏心率可大幅提高其稳定性，浮环轴承具有极好的稳定性，在航空航天等领域具有广阔的应用前景。

［1］康召辉，任兴民，黄金平，等.浮环轴承系统中浮动环作用机理研究［J］.振动工程学报，2009，5（22）：533-537.

KANG Zhao-hui，REN Xing-min，HUANG Jin-ping，et al.Research of mechanism of a floating ring in the floating ring bering system［J］.Journal of Vibration Engineering，2009，5（22）：533-537.

［2］万 召，孟 光，荆建平，等.燃气轮机转子-轴承系统的油膜涡动分析［J］.振动与冲击，2011，30（3）：38-41，52.

WAN Zhao，MENG Guang，JING Jian-ping，et al.Analysis on oil whirl of gas turbine rotor-bering system［J］.Journal of Vibration and Shock，2011，30（3）：38-41，52.

［3］岑少起，郭 红，薛东岭，等.透平膨胀机组动静压浮环轴承稳定性研究［J］.机械强度，2002，24（1）：32-34.

CEN Shao-qi，GUO Hong，XUE Dong-ling，et al.Stability study of radial-thrust floating-ring hybrid bearing［J］.Journal of Mechanical Strength，2002，24（1）：32-34.

［4］成 玫，孟 光，荆建平.转子-轴承-密封系统的非线性振动特性［J］.上海交通大学学报，2007，41（3）：398-403.

CHENG Mei，MENG Guang，JING Jian-ping.The nonlinear dynamical behaviors of a rotor-bearing-seal system［J］.Journal of Shanghai Jiaotong University，2007，41（3）：398-403.

［5］吕延军，虞 烈，刘 恒.流体动压滑动轴承-转子系统非线性动力特性及稳定性［J］.摩擦学学报，2005，25（1）：61-66.

LU Yan-jun，YU lie，LIU Heng.Stability and nonlinear dynamic behavior of a hydrodynamic journal bearing-rotor system［J］.Tribology，2005，25（1）：61-66.

［6］郭建萍，邱鹏庆，崔 升，等.有限长轴承非稳态油膜力建模及非线性油膜失稳［J］.振动工程学报，2001，14（1）：7-12.

GUO Jian-ping，QIU Peng-qing，CUI Sheng，et al.Study on unsteady nonlinear oil-film force model for finite journal bearings and it＇s oil-film whil analysis［J］. Journal of Vibration Engineering，2001，14（1）：7-12.

［7］ Guo H，Lai X M，Cen S Q，Theoretical and experimental study of constant restrictor deep/shallow pockets hydrostatic/hydrodynamic conicalbearing［J］. ASME， Journalof Tribology，2009，131（4）：041701-041707.

［8］Ene N M，Dimofte F，Keith J T G.A stability analysis for a hydrodynamic three-wave journal bearing［J］.Tribology International，2008，41：434-442.

［9］杨金福，杨 昆，付忠广，等.转子滑动轴承系统中油膜谐波振荡过程的试验研究［J］.燃气涡轮试验与研究，2007，20（3）：42-47.

YANG Jin-fu， YANG Kun， FU Zhong-guang， etal.Experimental rearch on the harmonic oil whip in sliding bearing-rotor system［J］.Gas Turbine Experiment and Research，2007，20（3）：42-47.

［10］康召辉，任兴民，王 鸷，等.浮环轴承系统中浮动环涡动运动研究［J］.振动与冲击，2010，29（8）：195-197.

KANG Zhao-hui， REN Xing-min， WANG Zhi， et al.Research of floating ring whirl in the floating ring bering system［J］.Journal of Vibration and Shock，2010，29（8）：195-197.

［11］ Guo H，Lai X M，Wu X L，et al.Performance of flat capillary compensated deep/Shallow pocketshydrostatic/hydrodynamicjournal-thrustfloating ring bearing［J］.Tribology Transcations，2009，52（2）：204-212.