序数空间中企业战略风险与企业绩效关系研究——基于中国纺织业面板数据分析

朱慧明，张晓昱，吴宣明，廖 萍

（湖南大学工商管理学院，湖南长沙 410082）＊

一、引言

企业发展战略关系着企业的生存与兴衰，企业的战略决策与其经营风险及竞争优势有着密切的关系［1］。什么样的战略可以获得高的绩效是非常吸引人的问题，而在企业的生存发展中，企业战略风险与绩效之间的关系一直是战略管理研究中的一个重要问题。

战略风险的概念由Andrews在1971年提出，将战略与风险理论结合，Barton等（1997）分别从管理决策、行业竞争排名、公司业绩和战略实施能力的不确定性等角度对战略风险进行了界定［2］。王国顺和李灿（2005）考虑四个指标建立战略业绩评价指标体系进行绩效评价和分析［3］。刘建国（2006）给出了基于属性空间分布的定量分析方法，对战略风险进行了评估［4］。很多学者把传统经济领域的“风险收益”关系问题提升到组织的层次来检验战略风险与收益的关系，结合行为理论对相关实证结果进行解释，并且试图把战略风险纳入到企业竞争优势的分析框架中。Bowman通过选择美国85个产业来验证公司战略风险与收益的关系，得到了大部分产业风险与收益呈负相关关系的重要结论，被称为“风险收益悖论（paradox）”［5］。Bowman的这个重要发现开辟了战略管理研究组织风险收益的新领域。Winfrey和Budd（1992）研究发现，风险和收益可能是独立的，不同的战略方案带来的风险与其收益的关系并不明显［6］。McGahan（1999）利用百分比将相关关系的正负性表示出来［7］。Ruefli和Wiggins（2003）利用非参数方法对企业业务影响，经营业绩进行了评价并对其战略风险进行了度量［8］。这些在基数空间采用传统均值方差方法对企业的战略风险和收益及其他绩效指标关系的研究有一定的局限性，没有考虑到企业之间的相互作用。因此，Collins和Ruefli（1992）提出借鉴序数空间熵值法对企业战略风险进行刻画，并对企业战略风险和收益进行了肯氏检验，得到企业的战略风险与收益存在负相关关系［9］。祝志明，杨乃定等（2008）利用中国沪深300数据通过最小二乘回归在中国背景下对勃曼悖论进行了验证［10］。而Powell（2010）在序数空间中给出排序的具体数值表，并通过对12个工业公司40年的数据验证［11］。但他们均采用的是横截面数据，并没有在时间维度上对战略风险和收益及其他绩效指标进行分析。朱承亮，岳宏志（2009）通过建立面板数据模型对战略实施绩效进行了评价［12］，因此，将面板数据模型应用于战略经济学的研究成为今后研究的主要方向。

针对上述问题，本文将序数空间定义的战略风险与面板数据模型结合对企业风险和收益的关系进行研究，收集中国纺织业的相关数据，通过借鉴序数信息下系统组织整体不确定性度量的熵法，对企业的战略风险进行刻画，并利用分阶段数据，建立随机效应面板数据模型，选取企业绩效中的四个指标，对战略风险和它们的相关关系进行实证检验，对公司的战略选择及投资决策具有指导意义。

二、序数空间中战略风险的刻画

以往的研究中多采用计算净资产收益率的均值方差的方法来度量企业的风险值，而这种方法将损失和收益同等看待，企业的持续损失或收益都将被看作风险计算。其次，均值方差方法用企业自身收益的绝对变动对风险进行度量，忽略了企业之间的相互作用及其在一个参考系统中排名相对位置变化带来的影响。另外，均值方差的方法一般利用独立于时间的横截面数据计算，而企业的战略风险往往和时间密切关联。因此，为避免均值方差方法带来的局限，可从序数空间角度出发。

将同行业的企业看作一个系统参考集，通过研究不同时期内各阶段企业排名的变化，引起的系统结构的变化带来的不确定信息用熵度量，采取时间窗的方式对已有数据进行处理，将5年当作一个时间段进行研究，滚动进行相关分析，避免了偶然性的干扰。

（一）构建转移概率矩阵

假设一个战略系统参考集中n个公司持续经营，在研究的时间段内无退出和进入现象，公司的所有指标值在研究的单个时间段内保持不变。

假设第i个公司从t0到tm时间段，指标排名由j到k，系统中公司在一个研究的阶段的排名变化矩阵设为Φi，由第i个公司排名变化次数φijk组成矩阵Φijk。如果排名无变化，则记为0。将公司排名转移矩阵中每个元素除以其行和，得到该时间段内公司在系统中排名的转移概率矩阵如下：

此处，Φ·jk是n个公司在t0到tm时间段内所有从j变到k的值；Φ·j·是矩阵Φ＝（Φ·jk）n×n中第i行和。由此得到转移概率矩阵P＝（p·jk）n×n，其中，pj·、p·k分别表示行与列之和，取值均为1。

（二）不确定系统中加权熵值度量

在不确定系统中，信息和熵都是表示系统状态的物理量，信息描述的是系统的有序程度，而熵是描述系统的无序程度。一个系统要从无序变为有序必须减少熵，而增加信息量，则可借用熵度量的方法，用概率分布矩阵描述一个不确定系统的平均条件熵。

但由于实际战略参考系统中其竞争位置排名变动的方向和幅度不同，会出现转移事件是在一个转移系统中转移即由两个不相邻的状态转移而来，而每个位置的转移均有所不同。例如，从排名第一转移到排名最后一名和由排名倒数第二名转移到最后一名，对于系统中熵值的影响是不同的。元素的转移和它发生的概率有关，和排名的变化也有关，故每次转移在转移概率矩阵中所占的比重不同，因此应设定权重矩阵对风险熵值进行度量。

选择权重值基于以下的假设，假设1，权重值均为非负有限实数。假设2，如果一个时段的转移A比另个时段转移B重要，那么它们的权重ωA和ωB有：ωA＞ωB。构建权重函数衡量转移概率矩阵：

此处，α／β＝1，α表示在状态转移过程中变动幅度的固定系数，按研究的时间段划分来取值，一般按年取时间段通常为1，按半年取时间段则通常取0．5，β表示状态转移变化后企业排名的变化，若状态转移后，企业位置排名不变，即j＝k时，权重为β，通常取β＝1。根据对风险的界定，负面的不确定性即排名损失的改变才能称为风险，对战略系统而言，k＞j时，排名从高到低转移，意味着企业的竞争位置相对下降，所有的不确定信息为系统战略风险。因此加权不确定系统风险熵可以定义为：

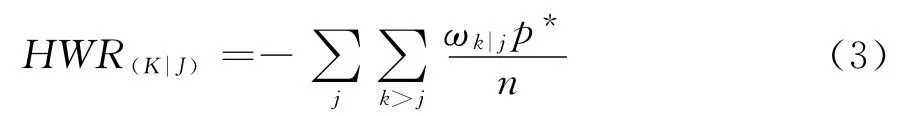
其中

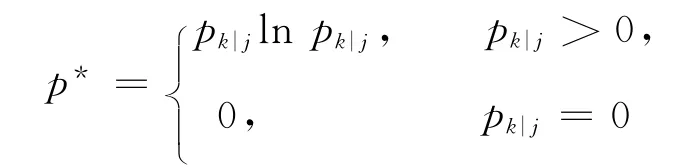
在无权重系统中，转移概率矩阵中每个元素相等是可以得到系统的最大熵值，加权系统中比无权重系统计算最大熵相对困难，Thomas（1979）和Freund（1984）采用数学中优化方法得到加权系统的最大熵。

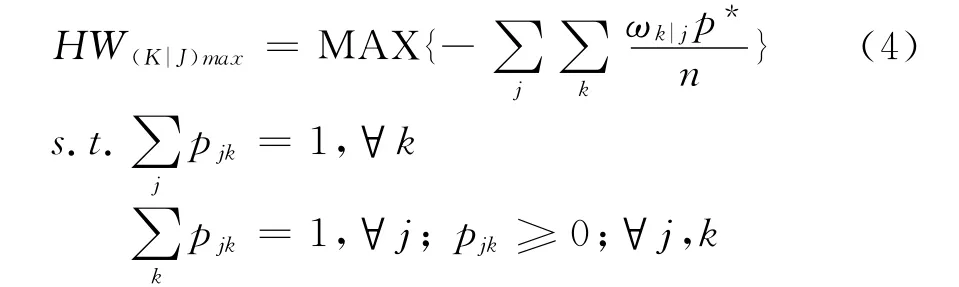
（三）单个企业战略风险度量

考虑每个公司对整个系统战略风险的贡献度，可以得到每个企业在系统战略风险中与战略参考集中其他企业的贡献关系和排名，在特定的状态转化中，记单个企业的转移次数为fijk，那么它对整个状态转移次数的贡献成正比，即：fijk／f·j·，所以单个企业的加权平均条件熵可记为：hWi（K｜J）＝ωk｜jp＊＊，由此可得单个企业的风险为：

其中

将得到的单个企业的风险值与加权系统的最大熵相比，标准化得到单个企业在系统中的战略风险值：

由此，可以得到每5年阶段内，企业的战略风险值，由于该风险值采取净资产收益率的序数信息，与其本身的数值无关，并将损失和收益区别对待，对企业的持续损失和盈利都不考虑为风险。并利用滚动窗口将时间的影响因素在企业战略风险熵中表现出来，因此，利用序数空间熵理论得到的企业战略风险值用于对绩效指标的关系分析更为贴切。

三、面板数据模型的设定与估计

以往对企业绩效分析的研究中大多利用企业具有的二维信息，如利用若干企业绩效指标的时间序列建模或利用横截面数据建模，但在实际中仅利用二维信息的模型不能满足对战略风险与企业绩效关系的分析需要。因此，从面板数据出发研究实际战略风险与企业绩效关系问题可以构造和检验比以往单独使用横截面数据或时间序列数据更为真实的行为方程，进行更加深入的分析是可行且必要的。

（一）变量选择

根据前文分析，以信息熵度量的企业战略风险为因变量，企业净资产收益率、非流动资产周转率、总资产周转率、股息支付率为自变量，对其相关关系进行研究，变量选择如下：

（1）序数空间中企业战略风险（SR）：选取上市公司的净资产收益率（ROA）的序数信息，利用信息熵方法衡量企业战略风险（式6）。

（2）企业净资产收益率（ROA）：指公司税后利润除以净资产得到的百分比率，反映股东权益的收益水平，用以衡量公司运用自有资本的效率。

（3）非流动资产周转率（UCAR）：指销售收入与非流动资产的比值，反映非流动资产的管理效率。是资产负债表上资产总额减去流动资产后的期初期末的平均数。

（4）总资产周转率（TAT）：指企业在一定时期业务收入净额同平均资产总额的比率，用来考察企业资产运营效率，资产的周转次数越多或周转天数越少，表明其周转速度越快，营运能力也就越强，收益就越大，风险越小。在销售利润率不变的条件下，周转的次数越多，形成的利润越多，即反映了公司的盈利能力。

（5）股息支付率（DPR）：是向股东分派的股息占公司盈利的百分比，反映普通股股东从每股的全部净收益中分得多少。

（二）模型构建

Cheng Hsiao（1986）提出利用面板数据进行经济分析，含有个体、时间、指标的三维信息，结合上文对变量的分析，建立战略风险和企业绩效关系面板回归方程模型如下：

此处ROAit，UCARit，TATit，DPRit为k×1向量，β1，θ1，γ1，λ1为1×k向量，k为解释变量的数目，E（uit）＝0，Var（uit）＝σ2it。i，t分别为截面维度与时间维度，αi为截距向量，uit为误差成分。在一维误差分解即固定效应模型中，uit＝μi＋νit或uit＝λt＋νit；在二维误差分解即随机效应模型中，uit＝μi＋λt＋νit，μi为横截面效应，λt为时间效应，νit为随机变量。在对该问题的实证研究过程中首先对模型进行Hausman检验，以确定采用随机效应或固定效应模型进行估计。

四、实证研究与结果分析

（一）样本与数据来源

纺织业在我国是一个劳动密集程度高和对外依存度较大的产业。目前，全球纺织业市场前景不确定性日益增高，这与全球信用危机以及美国、欧盟经济增长减缓的趋势一致。国际纺织、服装贸易制度的变化使纺织服装企业面临了新的挑战，这对我国纺织业不仅带来了希望和机遇，同时也带来了极大风险。因此选取我国32家纺织业企业，以2001年为研究起始日期，2009年作为截止日期，确定为研究的样本。通过收集2001～2009年期间这32家企业年报数据，构成本文研究的企业战略参考集，数据来源为国泰安数据库（http：／／www．gtarsc．com）。

选取企业净资产收益率构成的战略参考集进行分析，通过序数方法进行排名，得到研究期内32家纺织企业的绝对收益表，并以此计算单个企业在战略参考集中的序数战略风险。以5年为一阶段，研究2001～2009年共划分为5个阶段，由于采用的是序数信息，所以年报中企业净资产收益率计算周期的差异不影响研究结果。

（二）实证结果分析

首先，对32家纺织业企业在9年中企业净资产收益率排名转移情况进行分析（图1），从图中可以看出：净资产收益率排名转移跳动较大，说明它对系统的稳定性影响较大，但排名下降的转移次数和排名上升的转移次数并不完全对等，即并不是有企业排名下滑就一定有企业排名上升，说明企业的战略风险除了与本身的排名下滑有关还与其他因素如绩效指标、外部环境等有密切的关系。

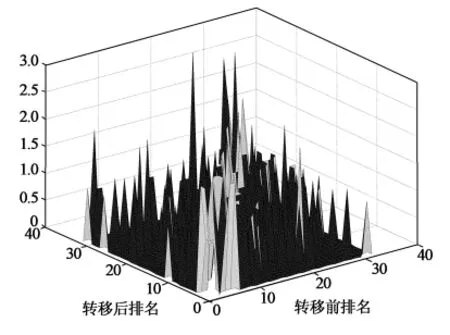
图1 净资产收益率排名转移图

将得到的企业战略风险值，和每个阶段净资产收益率、非流动资产周转率、总资产周转率、股息支付率五年的平均值进行统计量描述和分阶段相关性检验（表1）。

从表中可以看出，分阶段进行指标的相关性检验可以得到战略风险和各指标之间多成负相关关系，但各个指标间也存在相关性。而在每一年的相关性检验时，战略风险与各个绩效指标相关性并不明显，由于相关系数的缺点，即它接近于1的程度与数据组数n相关，这容易给人一种假象。在每一年的横截面数据中，当n较小时，相关系数的波动较大，此时仅凭相关系数较大就判定变量之间有密切的线性关系是不妥当的，因此，采取三维面板数据建模是必要的。利用公式（7）将5个阶段的数据建立面板数据模型，首先对其进行Hausman检验，得到随机效应模型好于固定效应模型的概率为89．13%，因此，选用随机效应模型进行估计，结果见表2。

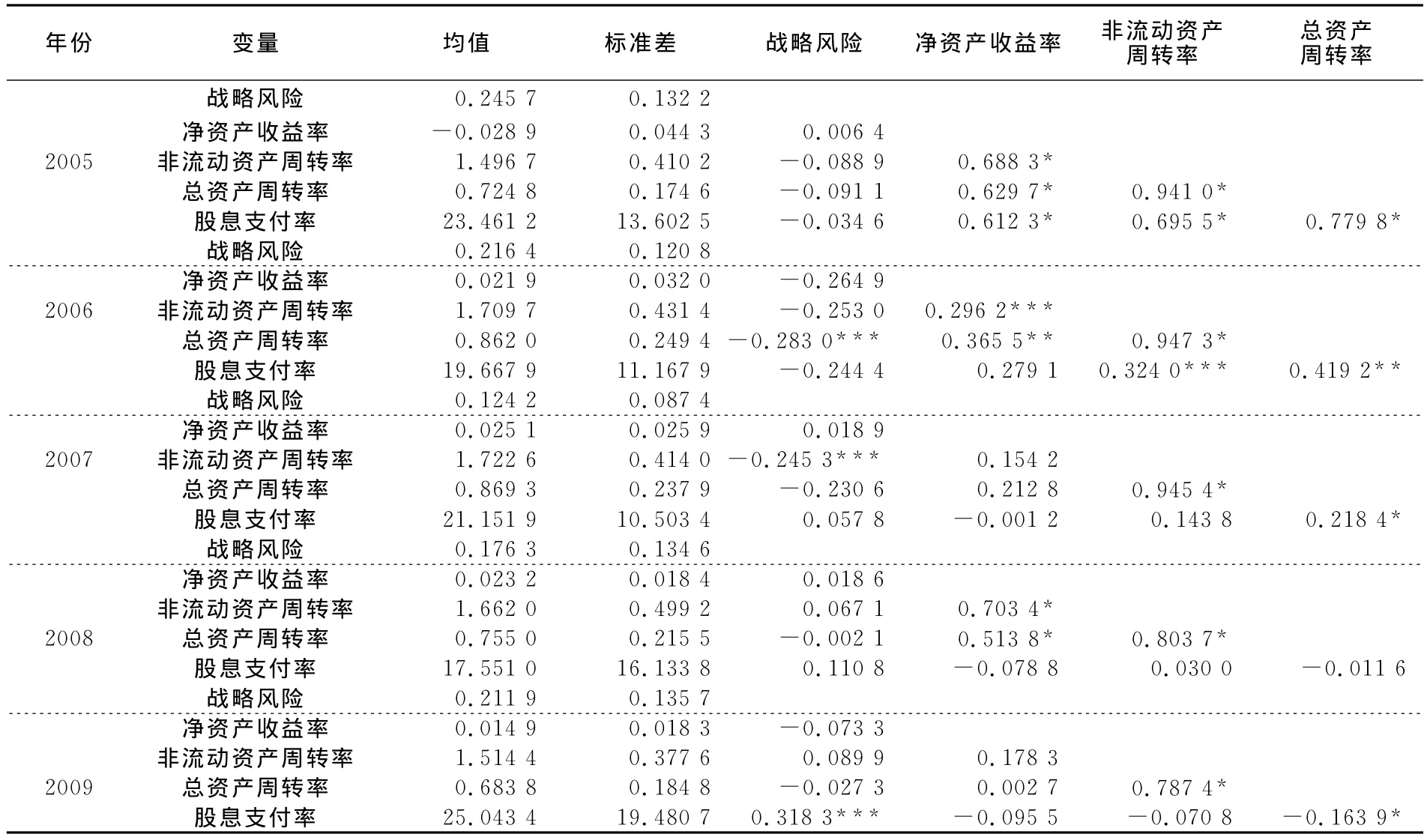
表1 统计量描述和分阶段相关性检验

从表1可以看出，战略风险和企业的净资产收益率呈负相关关系，在5%显著水平下通过检验，这说明较高的战略风险不一定带来较高的收益，相反，高收益低风险的情形是存在的，而取得高收益的企业是其在一定区间内的战略参考集中排名下降次数相对较少的，收益较低的企业是由于其绩效排名下滑频繁造成的。风险与收益的关系说明企业之间的异质性明显，在全球纺织业不确定性日益升高的情况下，负相关关系则为中国纺织企业的战略选择提供了相关的理论依据。战略风险和企业的非流动资产周转率呈正相关关系，表明非流动资产的管理效率对战略风险的影响是正面的，也就是说明非流动资产的管理效率越高带来的风险越大。和总资产周转率的负相关关系表明对于企业来讲较高的盈利能力不一定带来较高的风险，追求在低风险下的利润最大化存在了可能性。和股息支付率正相关系数较小，说明向股东分派的股息占公司盈利的百分比对企业的战略风险影响较小。

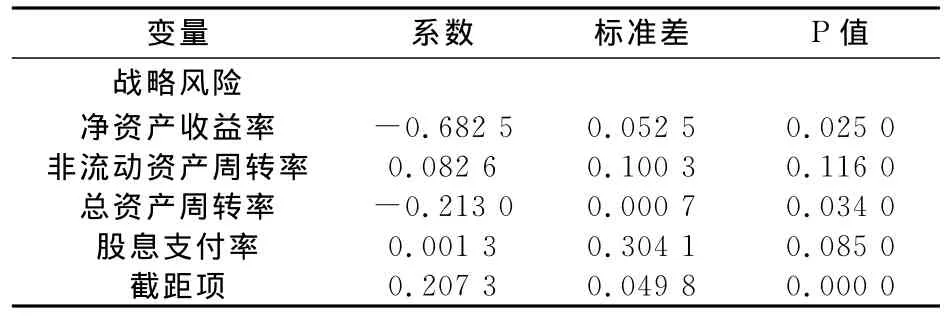
表2 战略风险对各个指标的面板回归结果

五、结 论

以上针对传统的均值方差、资本资产定价等一般度量方法的局限性，从序数空间理论出发，借鉴序数理论中对系统不确定性的熵度量方法，将企业参考集的战略风险考虑为系统内排名位置的变化，通过把战略风险转化为企业在战略参考系统内收益排名的下降带来的负面不确定信息，给出了序数战略风险度量的一般模型。同时，采取滚动窗口分析方法将研究阶段划分为5个阶段，并采用面板数据建立随机效应面板数据模型。选取纺织业32家企业为研究对象，取净资产收益率、非流动资产周转率、总资产周转率、股息支付率五年的平均值为解释变量，模型分析结果表明我国纺织业战略风险和企业的净资产收益率及总资产周转率呈负相关关系，和企业非流动资产周转率、股息支付率虽呈正相关关系，但相关系性较小，验证了在中国国情下纺织业“勃曼悖论”的存在，为中国纺织企业做出正确的战略决策及企业的长期发展规划提供了理论基础。采用序数空间的熵度量企业战略风险，结合面板数据模型分析，不仅可以克服传统方法的缺点，更贴合了战略风险的内涵，对企业的战略实践和选择具有稳健的指导意义。

［1］Fiegenbaum A，Thomas H．Strategic risk and competitive advantage：an integrative perspective［J］．European Management Review，2004，1（1）：84－95．

［2］Frank，L．Winfrey．，James，L．Budd．Reframing strategic risk［J］．SAM Advanced Management Journal，1997，62（4）：256－272

［3］王国顺，李灿．建立战略业绩评价指标体系的基本思路［J］．财经理论与实践．2005，26（3）：113－116．

［4］刘建国．基于属性测度的企业战略风险评价［J］．统计与决策，2006，（3）：142－143．

［5］Bowman E H．A risk／return paradox for strategic management［J］．Sloan Management Review，1980，21（3）：17－31．

［6］Winfrey，Budd．A framework for integrated risk management in international business［J］．Journal of International Business Study，1992，（2）：311－329．

［7］McGahan A M．The performance of U．S．Corporations：1981－1994［J］．Journal of Industrial Economics，1999，47（4）：373－398．

［8］Ruefli T W，Wiggins RR．Industry，corporate and businesssegment effects and business performance：a non－parametric approach［J］．Strategic Management Journal，2003，24（9）：861－879．

［9］Collins J M，Ruefli T W．Strategic risk：an ordinal approach［J］．Management Science，1992，38（12）：1707－1731．

［10］祝志明，杨乃定，高婧．战略风险与收益：中国上市公司的实证研究［J］．财经研究．2008，34（5）：133－143．

［11］Powell T C，Reinhardt I．Rank friction：an ordinal approach to persistent profitability［J］．Strategic Management Journal，2010，31（5）：1244－1255．

［12］朱承亮，岳宏志，李婷．基于Ja M视角的西部大开发战略实施绩效评价［J］．科学学研究，2009，27（11）：1162－1167．