非惯性系动力学定理中无惯性力作用项的条件确定

林景波

（延边大学理学院 物理系，吉林 延吉133002）

非惯性系动力学定理中无惯性力作用项的条件确定

林景波

（延边大学理学院 物理系，吉林 延吉133002）

在随动点o′平动的非惯性系中，运用理论研究法建立相对动点o′的动力学普遍定理，发现这些定理中均含有惯性力的作用项，使得普遍定理的运用受到限制.为解决这一问题，通过分析惯性力作用项的特征和动点o′的选取，提出了定理中无惯性力作用项的条件，使平动非惯性参照系问题的动力学方程得以简化.

非惯性系；动点；动力学定理；惯性力

取随动点o′平动的非惯性参照系研究问题，并建立非惯性坐标系o′－x′y′z′，如图1所示.相对动点o′运用相关动力学理论，列出动力学普遍定理：动量定理、角动量定理、动能定理，在这3个定理的表达式中分别出现了惯性力、惯性力矩、惯性力的功，即表现出惯性力的作用；因此，当将这些定理运用于平动的非惯性系中解决力学体系问题时，遇到所列方程较为复杂，甚至无法求解的问题.经查阅文献［1－6］发现，相关研究仅限于非惯性系中动力学普遍定理的建立，而未涉及如何消除普遍定理中惯性力作用项影响的研究.鉴于此，本文在建立相对动点o′的动力学普遍定理的基础上，分析定理中所含惯性力作用项的特点，提出了如何选取动点，使动力学普遍定理中不再出现惯性力作用项，得到所列方程能够简化的条件，为平动非惯性系中力学体系问题的解决提供了有效方法.

图1 非惯性参照系o′－x′y′z′

1 动量定理中无惯性力作用项的条件确定

如图1所示，任意质点mi对固定坐标系oxyz的位置矢量为ri＝ro′＋r′i，则有vi＝˙ri＝˙ro′＋˙r′i＝vo′＋˙r′i，整个质点组对固定坐标系oxyz的动量为

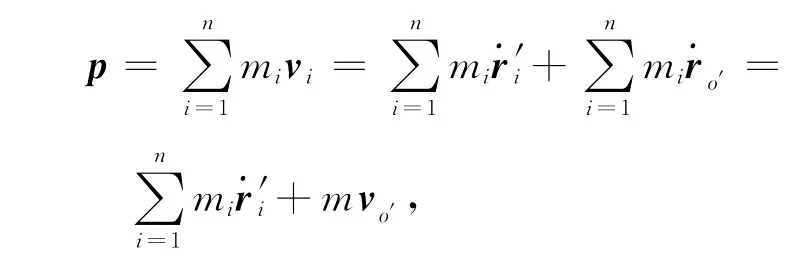
式中出现了惯性力作用项－mao′，即惯性力.

适当选取动点o′使或－mao′＝0，则（1）式中将不出现惯性力.据此对所需满足的条件做如下分析：

1）当选取的动点o′与质点组质心c重合时，由于质心加速度与动点加速度相等，即ac＝ao′，根据质心运动定理式可变为这表明质点组相对质心（选取的动点o′）的动量对时间的变化率恒为零，与外力和惯性力无关.

2）当质点组是1个刚体，且选取的动点o′为加速度瞬心时，有ao′＝0，则有惯性力－mao′＝0.由此（1）式变为，表明已无惯性力作用项.

3）当选取的动点o′做匀速直线运动时，有动点ao′＝0，使得惯性力－mao′＝0.由此（1）式变为，表明已无惯性力作用项.

2 角动量定理中无惯性力作用项的条件确定

如图1所示，在随o′平动的非惯性坐标系o′－x′y′z′中建立对动点o′的角动量定理［3］

式中r′c为质点组的质心c对o′的位置矢量，而r′c×（－m¨ro′）则为惯性力作用项，即惯性力对o′点的力矩矢量和，称之为惯性力矩.

如果使（2）式中不出现惯性力矩r′c× （－m¨ro′）项，则要求r′c×（－m¨ro′）＝0.据此对所需满足的条件做如下分析：

1）当选取的动点o′的加速度¨ro′与r′c平行时，r′c×（－m¨ro′）＝0.以均质圆柱在粗糙平面上做纯滚动为例加以说明，如图2所示.设圆柱与平面的接触点为A，则A点为圆柱运动的速度瞬心，当取A点为动点o′时，则A点的加速度（动点o′的加速度）指向质心c（圆心），这使得质心c对A点（动点o′）的位置矢量r′c平行于A点的加速度¨rA.此时选取A点为动点o′有r′c×（－m¨ro′）＝0，于是（2）式中将不出现惯性力矩项.

图2 均质圆柱在粗糙平面上做纯滚动

2）当选取的动点o′与质点组质心c重合时，因r′c＝0，则有r′c×（－m¨ro′）＝0.

3）当选取的动点o′做匀速直线运动或质点组为刚体且取o′为加速度瞬心时，因动点o′的加速度为零，即¨ro′＝0，则有r′c×（－m¨ro′）＝0.

3 动能定理中无惯性力作用项的条件确定

如图1所示，在随o′平动的非惯性坐标系o′－x′y′z′中，质点组的任意质点mi相对此动坐标系的动力学方程为［5］

两边乘以dr′i得dr′i，则可推得.对于由n个质点所组成的质点组，便有

式（3）表明质点组相对o′的动能变化不仅与体系外力、内力作功有关，而且还与惯性力作功有关，即出现了惯性力作用项

1）当选取的动点o′的加速度垂直于dr′c时，m以均质圆盘在粗糙斜面上做纯滚动为例加以说明，如图3所示.设圆盘与斜面的接触点为A，如果将其选为动点o′，由于A点（o′点）的加速度与斜面垂直，而圆盘质心c相对于A点（o′点）的位移dr′c则与斜面平行，所以此时有或满足了，即在（3）式中不出现惯性力的功.

图3 均质圆盘在粗糙斜面上做纯滚动

2）当选取的动点o′与质点组质心c重合时，因此时质心c相对动点o′无位移，即dr′c＝0，且则有

3）当选取的动点o′做匀速直线运动时，由于动点o′无加速度，即，则有

［1］林富生.非惯性系动力学研究综述［J］.武汉理工大学学报：信息与管理工程版，2007，29（7）：68－69.

［2］A.Ⅱ.马尔契夫.理论力学［M］.北京：高等教育出版社，2006：267－269.

［3］李铁.非惯性系中的动量定理与动量守恒［J］.电子科技大学学报，2004，33（5）：624－625.

［4］Goldstein H，Poole C，Safko J.Classical Mechanics［M］.3rd ed.Pearson：Addison Wesley，2002：48－50.

［5］张素红，李子敬.平移非惯性系中的能量关系［J］.物理与工程，2008，18（2）：21－23.

［6］Luo S，Chen X，Fu J.Stability theorems for the equilibrium state manifold of nonholonomic systems in a noninertial reference frame［J］.Mechanics Research Communications，2001，28（4）：465－468.

Determining the conditions on the inertial－force－free term in kinetic theorem of non－inertial system

LIN Jing－bo
（DepartmentofPhysics，CollegeofScience，YanbianUniversity，Yanji133002，China）

It is found that the theorems contain inertial force terms when the general relative－to－moving－point dynamics theorems are theoretically established in non－inertial system translating with moving pointo′.The existence of the inertial force terms constrains the application of the general theorems.To solve the problem，based on the feature of inertial force term in the established general dynamics theorems，the choice of the moving pointo′is analyzed and the conditions on which there is no inertial force term in the theorems are given.

non－inertial system；moving point；kinetic theorem；inertial force

O131.3

A

1004－4353（2012）01－0047－03

2011－10－20

林景波（1965—），男，副教授，研究方向为理论物理.