Unruh单粒子态拥有左右成分时在振幅阻尼通道下的量子消相干

计 新

（延边大学理学院 物理系，吉林 延吉133002）

Unruh单粒子态拥有左右成分时在振幅阻尼通道下的量子消相干

计 新

（延边大学理学院 物理系，吉林 延吉133002）

研究了非惯性系中振幅阻尼通道下由Unruh效应引起的量子消相干现象.结果表明：当Unruh单粒子态拥有左右成分时，初始纠缠越大，共生纠缠度就越大，并且与Unruh单粒子态只有右成分时相比，纠缠受到了严重地衰减.

量子消相干；振幅阻尼；非惯性系

0 引言

自从爱因斯坦首次提出量子纠缠这一概念以来，人们对量子纠缠进行了广泛深入的研究.众所周知，量子纠缠是进行各种量子信息处理的重要物理资源，它在量子信息学的发展中起着非常重要的作用.然而，由环境引起的量子消相干不可避免地要引起量子纠缠的损失，从而使量子信息处理任务不能顺利地进行.为了更好地了解纠缠演化特性，人们对非惯性系下的量子纠缠进行了大量研究.Alsing和Milburn研究了非惯性系中的量子隐形传送，发现量子纠缠度降低了［1］.Fuentes－Schuller和 Mann证明了2个观察者通过探测2个自由玻色模中的1个就能决定2个模之间的纠缠［2］，并且发现，在非惯性系中，当观察者做相对加速运动时，初始处于最大纠缠的量子态的纠缠度降低，这说明在非惯性框架下纠缠是依赖于观察者的.Alsing等分析了自由狄拉克场2个模间的纠缠，发现纠缠度降低，并且在无限加速情况下纠缠渐近达到1个非零最小值［3］.Wang等研究了振幅阻尼通道下非惯性系的量子消相干［4］，发现在有限加速下就已经出现了纠缠死亡现象，并且加速越大纠缠死亡出现得越早.最近，Bruschi等分析了在非惯性系中研究纠缠常用的单模近似的有效性，揭示了正则分析中所用的纠缠态可以看成是1个Minkowski模和1个Unruh模的纠缠态，并且任何1个Unruh单粒子态都包含不同的左右成分.基于这一结果，本文将研究非惯性系中在振幅阻尼通道下由Unruh效应引起的量子消相干现象.我们将考虑不同初始的纠缠演化情况.

1 纠缠演化

假设2个观察者Alice和Rob初始共享纠缠态［5］

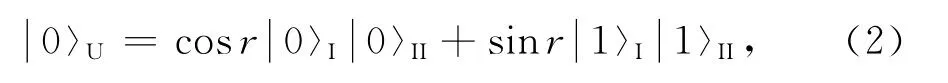
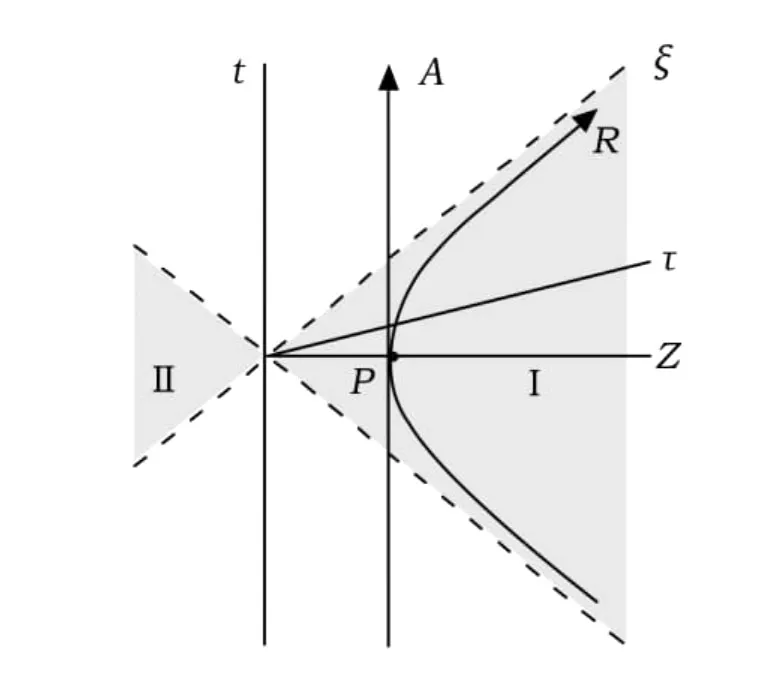
图1 Rindler时空图［4］：加速观察者Rob在区域I中沿着双曲线做加速度为a的匀加速运动，且与区域II无关

这里qR和qL是复数，满足为了方便，我们只考虑qR和qL是实数的情形.按照Alice的Minkowski模和Rob的Rindler模，利用方程（2）和（3），可以将方程（1）重写为

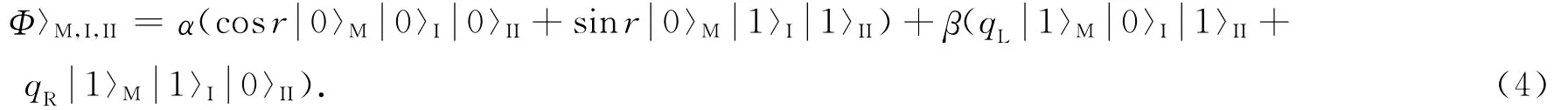
因为Rob与区域II不联接，信息编码在Alice描述的M模和Rob描述的I模上.那么，对区域II求迹可得

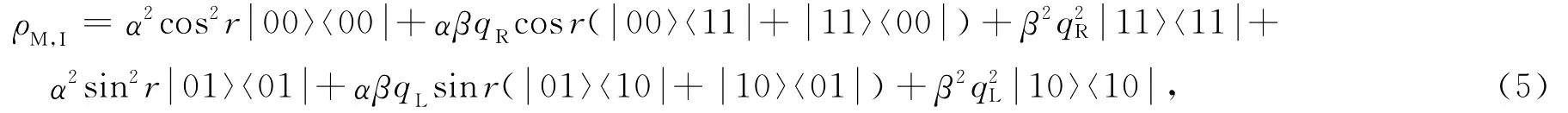
本文只考虑Rob的量子位与噪声环境相耦合的情形.在振幅阻尼通道下，这一过程可以描述成［6］：

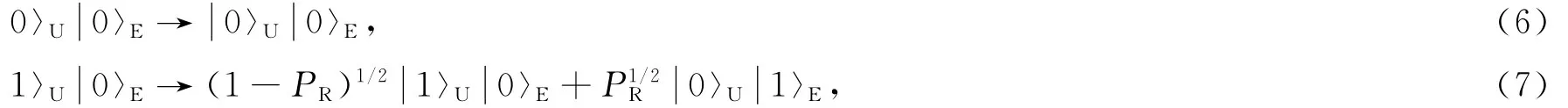
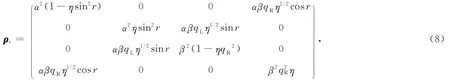
其中η＝1－PR.

由于2个量子位混合态的纠缠度可以方便地由共生纠缠Concurrence来量化，因此共生纠缠可以由量子位M和I的密度矩阵ρ计算得到，其定义［8－9］为

其中λ1／2i（λi≥λi＋1≥0）是矩阵ρs~ρs本征值的平方根，~ρs＝（σy⊗σy）ρ＊s（σy⊗σy）是矩阵（8）的自旋翻转矩阵，即

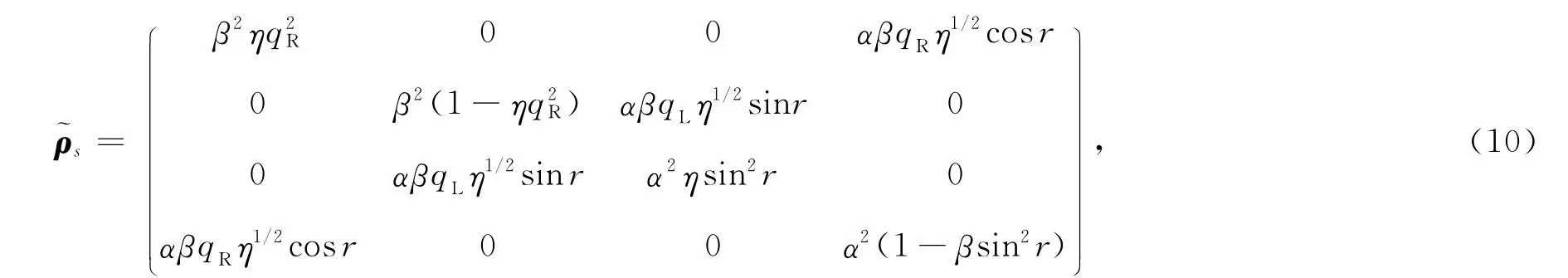
其中σy是泡利矩阵的本征值如下：

2 讨论与结论

图2 共生纠缠随衰变参数变化的关系曲线

图2为共生纠缠随衰变参数PR变化的关系曲线其中实线对应α＝1（图中没有显现，因为纠缠为零），点线对应，点划线对应.从图中可以看出，当考虑Unruh单粒子态具有左右成分时，对于相同的衰变参数，初始纠缠越大，共生纠缠越大，并且与Unruh单粒子态只有右成分相比［10］，纠缠受到了严重地衰减.在这种情况下，量子态已经不能用于量子信息处理.

［1］Alsing P M，Milburn G J.Teleportation with a uniformly accelerated partner［J］.Phys Rev Lett，2003，91：180404（4）.

［2］Fuentes－Schuller I，Mann R B.Alice falls into a black hole：entanglement in non－inertial frames［J］.Phys Rev Lett，2005，95：120404（4）.

［3］Alsing P M，Fuentes－Schuller I，Mann R B，et al.Entnaglement of dirac fields in non－inertial frames［J］.Phys Rev A，2006，74：032326（15）.

［4］Wang J，Jing J.Quantum decoherence in noninertial frames［J］.Phys Rev A，2010，82：032324（4）.

［5］Bruschi D E，Louko J，Martín－Martínez E，et al.Unruh effect in quantum information beyond the single－mode approximation［J］.Phys Rev A，2010，82（4）：042332（11）.

［6］Breuer H P，Petruccione F.The Theory of Open Quantum Systems［M］.Ne wYork：Oxford University Press，2002：373－380.

［7］Salles A，de Melo F，Almeida MP，et al.Experimental investigation of the dynamics of entangle－ment：sudden death，complementarity，and continuous monitoring of the environment［J］.Phys Rev A，2008，78：022322（15）.

［8］Wootters W K.Entanglement of formation of an arbitrary state of two qubits ［J］.Phys Rev Lett，1998，80：2245－2248.

［9］Coffman V，Kundo J，Wootters W K.Distributed entanglement［J］.Phys Rev A，2000，61：052306（5）.

［10］Zhang W P，Deng J F，Jing J L.Decoherence of entanglement on initial states under amplitude damping channel［J］.2010，eprint ar Xiv：1011.5700v2.

Quantum decoherence under amplitude damping with the Unruh single particle state having left and right components

JI Xin
（DepartmentofPhysics，CollegeofScience，YanbianUniversity，Yanji133002，China）

We investigate quantum decoherence under amplitude damping channel in noninertial frame.When the Unruh single particle state has left and right components，the bigger the initial entanglement is，the bigger the concurrence is，and the entanglement is degraded greatly compared with that when the Unruh single particle state only has right component.

quantum decoherence；amplitude damping；noninertial frame

O431

A

1004－4353（2012）01－0044－03

2012－01－12

计新（1965—），女，副教授，研究方向为量子光学与量子信息学.