带有正负系数的非线性偏差分方程的频密振动性

吴冬梅，陶元红

（延边大学理学院 数学系，吉林 延吉133002）

带有正负系数的非线性偏差分方程的频密振动性

吴冬梅，陶元红＊

（延边大学理学院 数学系，吉林 延吉133002）

利用数列频率测度的概念及其性质，讨论了一类带有正负系数的非线性偏差分方程，得到了此类偏差分方程的频密振动性准则.仅利用方程系数数列的水平集“频率测度”的概念，给出了偏差分方程解的频密振动的充分条件，并且准确刻画了解的振动频率.

偏差分方程；频密测度；频密振动性

0 引言

经典的振动概念已经不能准确描述数列的振动频率，为了更细致地刻画数列的振动性，田传俊等［1］首次引进了数列的频密测度的概念，并由此定义了数列的频密振动性.此后，朱志强等［2］定义了数列的频密正振动和负振动概念，更加完善了对数列的频密振动的描述.目前，关于差分方程解的频密振动性已有文献报道［3－9］.

本文将讨论如下非线性偏差分方程解的频密振动性：

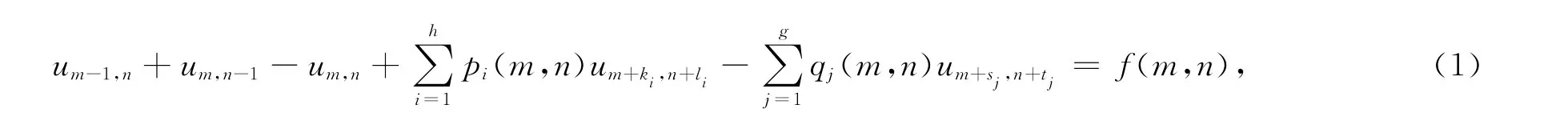
其中m，n∈Z［0，∞），pi（m，n）≥0（i＝1，2，…，h），qj（m，n）≥0（j＝1，2，…，g），并且满足如下条件：①ki，li（i＝1，2，…，h）；sj，tj（j＝1，2，…，g）均为非负整数；②pi＝ ｛pi（m，n）｝m，n∈Z［0，∞）（i＝1，2，…，h），qj＝ ｛qj（m，n）｝m，n∈Z［0，∞）（j＝1，2，…，h）以及f（m，n）均为实双序列.本文利用文献［1］中给出的频密测度概念，建立方程解的新频密振动准则，以更好地描述解的振动性质.设¯k＝max｛ki，sj｝＞0，¯l＝max｛li，tj｝＞0，ρ＝min｛um＋ki，n＋li｝，θ＝max｛um＋sj，n＋lj｝，σ＝max｛um＋ki，n＋li｝，τ＝min｛um＋sj，n＋lj｝，其中1≤j≤h，1≤j≤g.此外，还定义以下2个条件n）≥0.

1 预备知识

设Ω＝Z［－¯k，∞）×Z［－¯l，∞），对任意集合A，B⊆Ω，将A与B的并、交和差分别记为A＋B，A·B和A＼B.设Φ是Ω的1个子集，定义平移集XmΦ和YmΦ为：XmΦ＝ ｛（i＋m，j）∈Ω｜（i，j）∈Φ｝，YmΦ＝ ｛（i，j＋m）∈ Ω｜（i，j）∈ Φ｝.因此，XmYnΦ＝ ｛（i＋m，j＋n）∈ Ω｜（i，j）∈ Φ｝.

设α，β，λ，δ∈Z，且α≤β，λ≤δ，则Φ称为Φ（关于参数α，β，λ，δ）的导集，简记为容易证明

对任意的m，n∈Z［0，∞），令Φ（m，n）＝ ｛（i，j）∈Φ｜i≤m，j≤n｝.如果存在，称此极限为Φ的上频密测度，记为μ＊（Φ）.类似地，如果存在，称此极限为Φ的下频密测度，记为μ＊（Φ）.若μ＊（Φ）＝μ＊（Φ），则此极限记为μ（Φ），称为Φ的频密测度.显然μ（∅）＝0，μ（Ω）＝1，对任意Φ⊆Ω，有0≤μ＊（Φ）≤μ＊（Φ）≤1，如果Φ是有限的，那么μ（Φ）＝0.

引理1［1］对任意集合Φ，Γ⊆Ω，则μ＊（Φ＋Γ）≤μ＊（Φ）＋μ＊（Γ）；此外，若Φ和Γ是不相交的，则不等式μ＊（Φ）＋μ＊（Γ）≤μ＊（Φ＋Γ）≤μ＊（Φ）＋μ＊（Γ）≤μ＊（Φ＋Γ）≤μ＊（Φ）＋μ＊（Γ）成立，从而有μ＊（Φ）＋μ＊（Ω＼Φ）＝1.

引理2［1］对任意集合Φ，Γ⊆Ω，不等式μ＊（Γ）－μ＊（Φ）≤μ＊（Γ＼Φ）≤μ＊（Γ）－μ＊（Φ）和μ＊（Γ）－μ＊（Φ）≤μ＊（Γ＼Φ）≤μ＊（Γ）－μ＊（Φ）成立.

引理3［1］对任意集合Φ，Γ⊆Ω，有

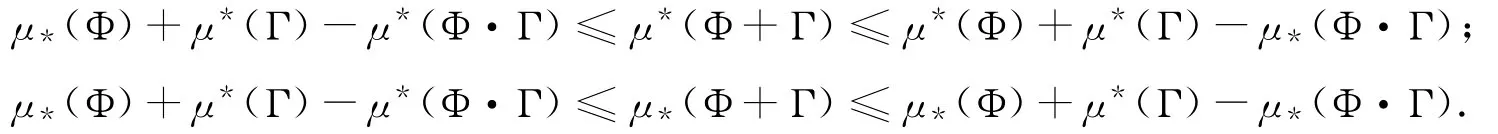
引理4［1］设Φ是Ω的1个子集，α，β，λ，δ∈Z，且满足α≤β，λ≤δ，那么

引理5［2］设 Φ1，…，Φn是 Ω的1个子集，则有

引理6［1］对任意集合Φ，Γ∈Ω，如果μ＊（Φ）＋μ＊（Γ）＞1，则集合Φ·Γ是无限集.

2 主要结论及其证明

对任意在Ω上的1个双序列｛vi，j｝，定义水平集｛（i，j）∈Ω｜vi，j＞c｝为（v＞c）.类似地，可以定义（v≥c），（v＜c）和（v≤c）.

定义1［1］设v＝ ｛vi，j｝（i，j）∈Ω是1个双序列.如果μ＊（v≤0）＝0，则称v是频密正的；如果μ＊（v≥0）＝0，则称v是频密负的；如果v既不是频密正的也不是频密负的，则称v是频密振动的.

对任意实双序列｛um，n｝，定义如下2个偏差分：Δ1um，n＝um＋1，n－um，n，Δ2um，n＝um，n＋1－um，n.

引理7 设um，n是方程（1）的解，若存在m0≥1，n0≥1，满足pi（m，n）≥0（i＝1，2，…，h），qj（m，n）≥0（j＝1，2，…，g），其中（m，n）∈Z［m0－1，m0＋2¯k］×Z［n0－1，n0＋2¯l］，则有：当um，n≥0，f（m，n）≤0时，Δ1um－1，n≥0，Δ2um－1，n≥0；当um，n≤0，f（m，n）≥0时，Δ1um－1，n≤0，Δ2um－1，n≤0.其中（m，n）∈Z［m0－1，m0＋¯k］×Z［n0－1，n0＋¯l］.

证明 当um，n≥0，f（m，n）≤0，（m，n）∈Z［m0－1，m0＋2¯k］×Z［n0－1，n0＋2¯l］时，由方程

定理1 假设

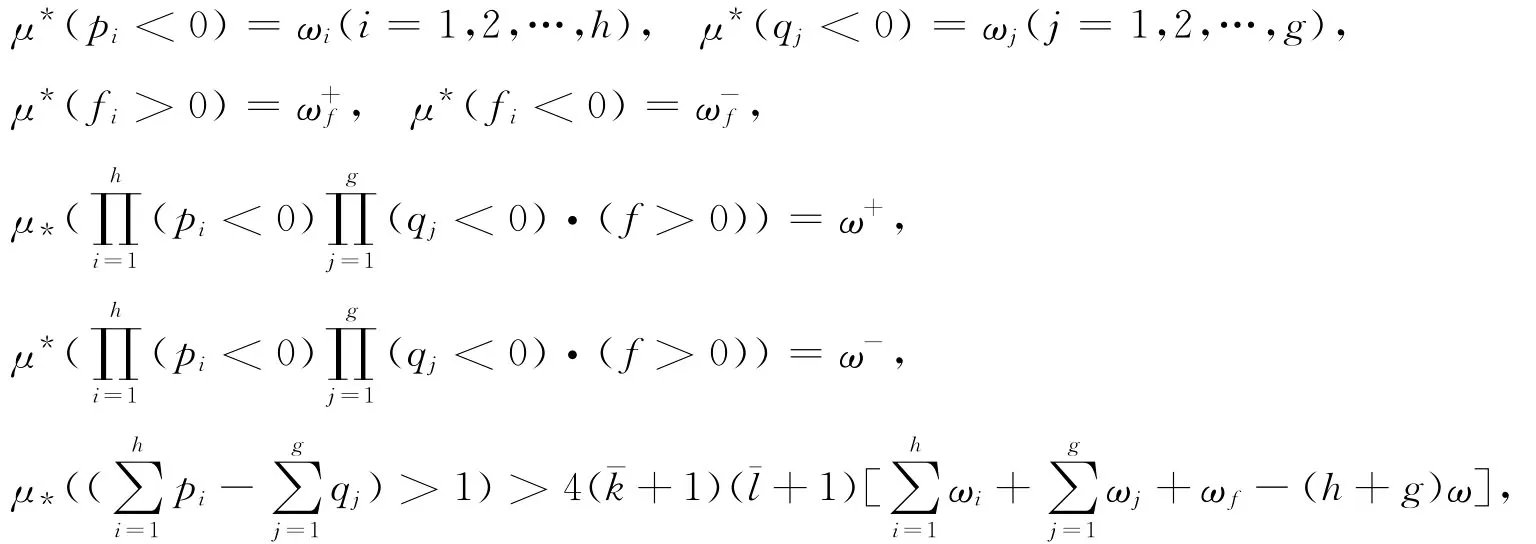
其中ωf＝max｛ω＋f，ω－f｝且ω＝max｛ω＋，ω－｝，那么方程（1）的每1个解都是频密振动的.

证明 首先，假设u＝ ｛um，n｝是方程（1）的频密正解，即μ＊（u≤0）＝0，则由引理1、4和5可知：

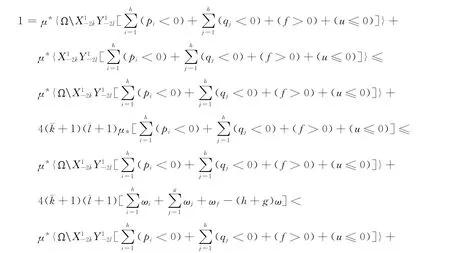
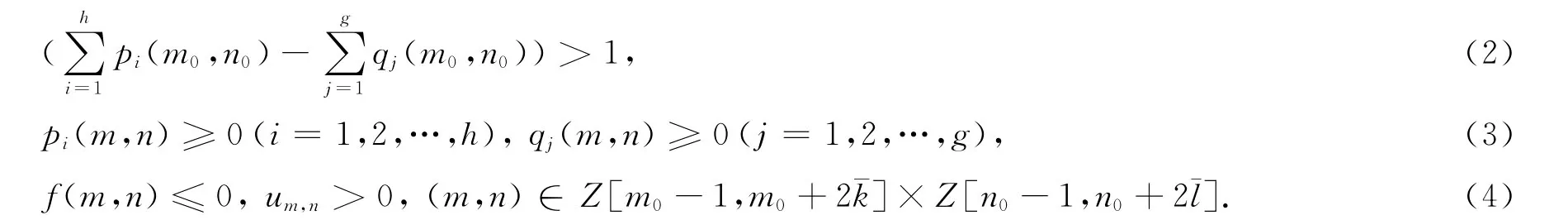
由式（3）、（4）和引理7可知：Δ1um－1，n≥0，Δ2um－1，n≥0，（m，n）∈Z［m0－1，m0＋¯k］×Z［n0－1，n0＋¯l］.再由式（3）、（4）和条件 ③ 得：0，由此得到矛盾.

其次，假设u＝ ｛um，n｝是方程（1）的频密负解，即μ＊（u≤0）＝0，类似于上述过程可以得到集合是无限集.与前面讨论类似，可以推出矛盾，因此结论成立.

定理2 假设

其中ωf＝max｛ω＋f，ω－f｝且ω＝max｛ω＋，ω－｝，那么方程（1）的每1个解都是频密振动的.

证明 首先，假设u＝ ｛um，n｝是方程（1）的频密正解，即μ＊（u≤0）＝0，则由引理1、4和5可知：

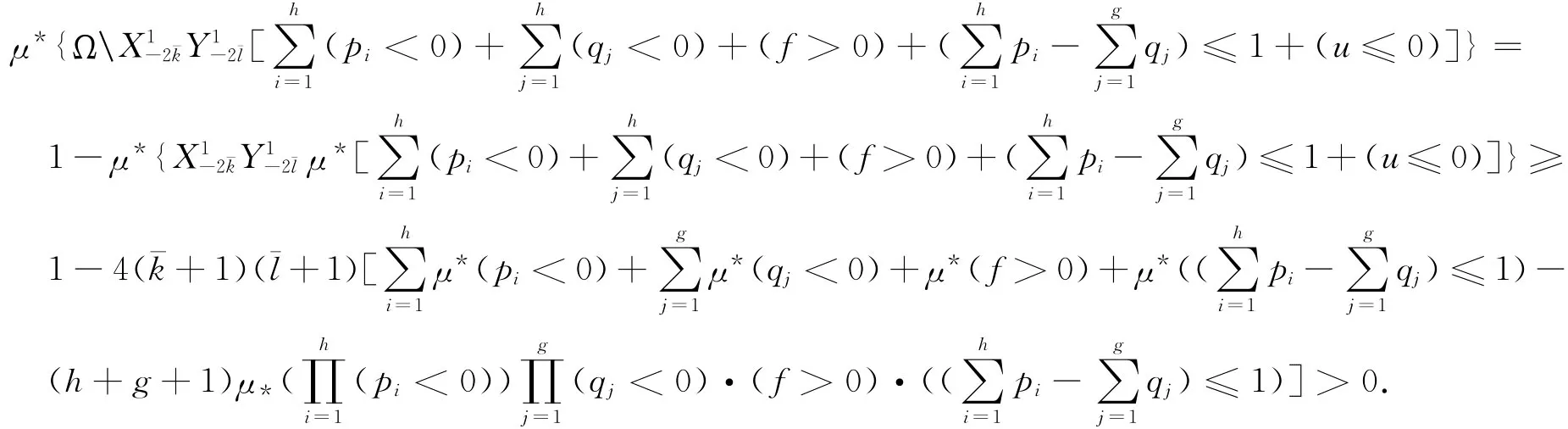
其次，假设u＝ ｛um，n｝是方程（1）的频密负解，即μ＊（u≥0）＝0.通过上述类似方法可得集合是无限集.由此得到矛盾，从而定理结论成立.

例 偏差分方程：

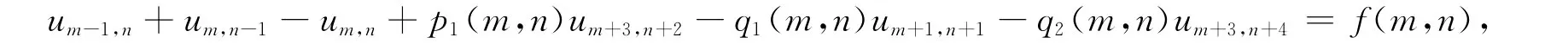
且μ＊（（p1－q1－q2）＞1）.此外，μ＊（（p1＜0）（q1＜0）（q2＜0）（f＜0））＝0，μ＊（（p1＜0）（q1＜0）1）ωf.那么由定理1或定理2可知，所给方程的任意解都是频密振动的.

［1］Tian Chuan－jun，Xie Sheng－li，Cheng Sui－sheng.Measures for oscillatory sequences［J］.Comput Math Applic，1998，36：149－161.

［2］Zhu Zhi－qiang，Cheng Sui－sheng.Frequently oscillatory solutions of neutral difference equations［J］.Southeast Asian Bulletin of Mathematics，2005，29：627－634.

［3］Cheng Sui－sheng.Partial Difference Equations［M］.London and Ne wYork：Taylor and Francis，2003：58－90.

［4］Tian Chuan－jun，Cheng Sui－sheng，Xie Sheng－li.Frequent oscillation criteria for a delay difference equation［J］.Funkcialaj Ekvacioj，2003，46：421－439.

［5］Zhu Zhi－qiang，Cheng Sui－sheng.Frequently oscillatory solutions for multi－level partial difference equations［J］.Internat Math Forum，2006，31：1497－1509.

［6］Yang Jun，Zhang Yu－jing.Frequent oscillatory solutions of a nonlinear partial difference equation［J］.J Comput Appl Math，2009，224：492－499.

［7］李冬梅，陶元红.一类非线性时滞偏差分方程的不饱和解［J］.延边大学学报：自然科学版，2010，36（2）：95－100.

［8］陶元红，李秀东.一类非线性时滞偏差分方程的频率振动解［J］.黑龙江大学自然科学学报，2010，27（5）：591－595.

［9］陶元红，吴冬梅.一类中立性差分方程的差频率振动性［J］.延边大学学报：自然科学版，2011，37（1）：42－45.

Frequent oscillation of a nonlinear partial difference equation with positive and negative coefficients

WU Dong－mei，TAO Yuan－hong＊
（DepartmentofMathematics，CollegeofScience，YanbianUniversity，Yanji133002，China）

By employing the concept and the properties of frequency measures of sequences，the frequently oscillatory behavior of the solutions for the nonlinear partial difference equation with positive and negative coefficients is discussed.Some ne woscillatory criteria are established.Only using the concept of“frequency measure”of the level sets of the involved parameter sequences in equation，the sufficient conditions of the solutions to be frequently oscillatory are presented，thus ho wfrequent the solutions oscillate is well described.

partial difference equation；frequency measure；frequently oscillatory criteria

O177.3

A

1004－4353（2012）01－0020－05

2011－12－05＊通信作者：陶元红（1973—），女，博士，副教授，研究方向为泛函分析及其应用.

国家自然科学基金资助项目（11161049）；吉林省自然科学基金资助项目（201215239）；延边大学科研项目（延大研科合字2011第7号）