一类奇异分数阶微分方程正解的存在性

王春来，侯成敏

（延边大学理学院 数学系，吉林 延吉133002）

一类奇异分数阶微分方程正解的存在性

王春来，侯成敏＊

（延边大学理学院 数学系，吉林 延吉133002）

研究了一类奇异非线性分数阶微分方程的边值问题.首先给出了该问题的格林函数和其所满足的一些性质，然后利用Krasuoselskii锥上的不动点定理和Leray－Schauder选择定理，建立了该方程至少存在1个正解的充分性条件.

正解的存在性；分数阶微分方程；不动点；锥

0 引言

由于分数阶微分方程被广泛应用于扩散与运输、混沌与湍流［1］、黏性弹力学及非牛顿流体力学［2］等领域，因此得到了学者们的广泛关注.在文献［3］中，Delbosco和Rodino利用Schauder不动点定理和Banach压缩原理研究了非线性微分方程Dα0＋u＝f（t，u），0＜α＜1的解的存在性，其中f∶［0，a］×R→R，0＜α＜＋∞是1个给定的在（0，a）×R上连续的函数.文献［4］的作者利用上下解方法研究了方程Dα0＋u＝f（t，u），0＜α＜1的正解的存在性，其中f∶［0，1］×［0，＋∞）→ ［0，＋∞）是给定的连续函数.最近文献［5］的作者研究了边值问题：Dα0＋u（t）＋f（t，u（t））＝0，0＜t＜1，u（0）＝u′（1）＝u″（0）＝0，其中2＜α≤3，Dα0＋u（t）是Caputo导数，f∶（0，1］×［0，＋∞）→ ［0，＋∞）是给定的连续函数且本文研究了非线性分数阶边值问题正解的存在性，其中2＜α≤3，Dα1－u（t）是Caputo导数，f∶［0，1）×［0，＋∞）→ ［0，＋∞）是给定的连续函数且即f在t＝1是奇异的.然后利用Krasuoselskii不动点定理及锥上的Leray－Schauder选择定理得到了问题（1）的2个结果，即正解的存在性.有关分数阶微分方程解的存在性定理及其应用可参阅文献［3，6－7］.

1 预备知识

我们先引入必要的概念和引理.

定义1［8］给定函数f∶（0，＋∞）→R的Riemann－Liouvilleα（α＞0）阶积分定义为：

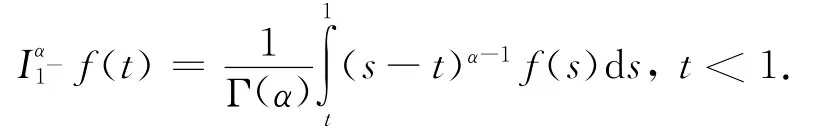
定义2［8］给定连续函数f∶（0，＋∞）→R的Caputoα（α＞0）阶导数定义为：

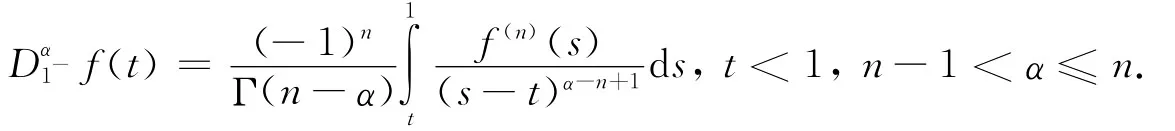
引理1［5］令n－1＜α≤n，u∈Cn［0，1］，则Iα0＋Dα0＋u（t）＝u（t）－C1－C2t－…－Cntn－1，其中Ci∈R，i＝1，2，…，n.

引理2 令n－1＜α≤n，u∈Cn［0，1］，则Iα1－Dα1－u（t）＝u（t）－C1－C2t－ … －Cntn－1，其中Ci∈R，i＝1，2，…，n.

证明 证明类似于引理1的证明，故从略.

引理3 给定f∈C［0，1］，且2＜α≤3，则方程

引理4［9］设E是1个Banach空间，P是1个锥，P⊆E，Ω1和Ω2是2个在E内圆心在原点的有界开球，且设是1个完全连续算子，使得：当x∈PI∂Ω1时有，当x∈PI∂Ω2时有；或者当x∈PI∂Ω1时有，当x∈PI∂Ω2时有成立，则A在中有1个不动点.

引理5［10］设E是1个Banach空间，且C⊆E是1个闭凸集.设U是C的1个相对开子集，且0∈U，是1个连续的紧映射，则A在中有1个不动点，或者存在u∈∂U和λ∈（0，1）使得u＝λAu.

2 主要结果及其证明

记E＝C［0，1］，且，则E是1个Banach空间.令P＝ ｛u∈E∶u（t）≥0，0≤t≤1｝，则P是1个锥，P⊆E.定义映射T∶P→P为

引理6 令0＜σ＜1，2＜α≤3，F∶［0，1）→R是连续的函数，且设（1－t）σF（t）在区间［0，1］上是连续的，则函数在区间［0，1］上也是连续的.

证明 易知H（1）＝0.以下分3种情况证明.

1）当t0＝1，∀t∈ ［0，1）.由于（1－t）σF（t）在区间［0，1］上是连续的，则存在M＞0使得因此

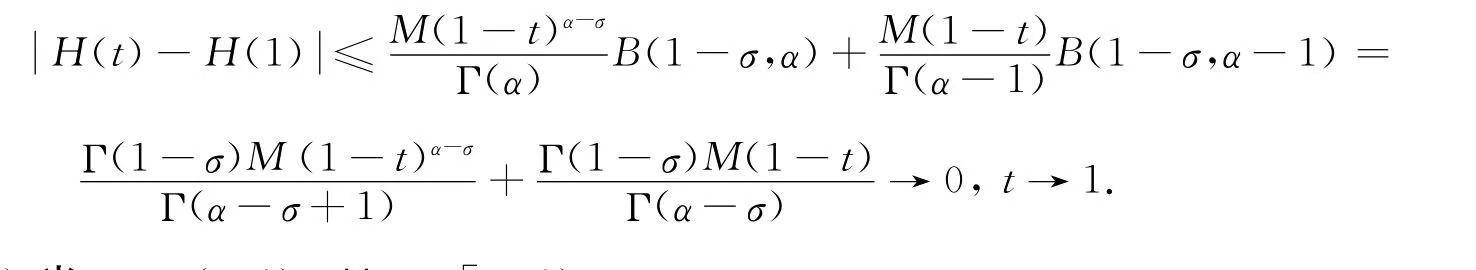
2）当t0∈ （0，1），∀t∈ ［t0，1）.

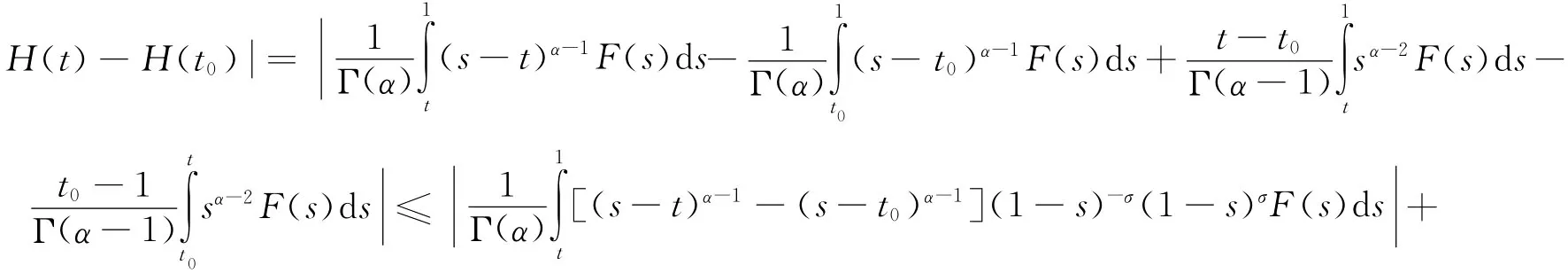
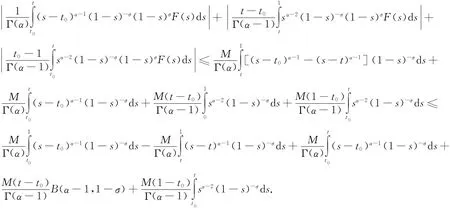
3）t0∈ ［0，1），t∈ ［0，t0）时，证明与情况2）类似，故省略.

引理7 令0＜σ＜1，2＜α≤3，f∶［0，1）×［0，＋∞）→ ［0，＋∞）是连续的函数，且·）＝ ∞.设（1－t）σf（t，u（t））在区间［0，1］×［0，＋∞）上是连续的，则由（3）式所定义的映射T∶P→P是完全连续的.

证明 对∀u∈P，由引理6和f，G（t，s）的非负性，知T是P→P是1个映射.令u0∈P并且若那么由（1－t）σf（t，u（t））的连续性，知（1－t）σf（t，u（t））在区间［0，1］×［0，C］是一致连续的.于是 ∀ε＞0，∃δ＞0（δ＜1），使得 ∀t∈ ［0，1］及u1，u2∈ ［0，C］，当时显然若那么对 ∀t∈ ［0，1］及有

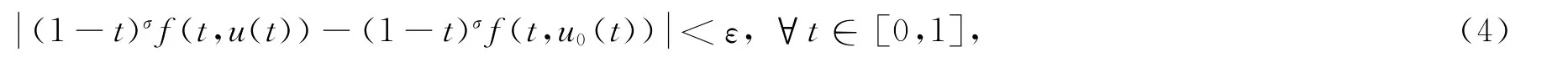
令M⊂P是有界的，即存在1个正数b使得对∀u∈M有于（1－t）σf（t，u（t））在区间［0，1］×［0，＋∞）上是连续的，令那么，故对于 ∀ε＞0，令，对于u∈M，t1，t2∈ ［0，1］，t1＜t2且0＜t2－t1＜δ，因此，T（M）是等度连续的.再由Arzela－Ascoli引理知是紧的，因此T∶P→P是完全连续的.

定理1设0σ＜1，2＜α≤3，f∶［0，1）×［0，＋∞）→［0，＋∞）是连续的，且＋∞，（1－t）σf（t，y）在［0，1）×［0，＋∞）上连续.假设存在2个不同的正的常数ρ和μ使得：

那么边值问题（1）至少有1个正解.

证明 由引理7可知T∶P→P是完全连续的.以下利用引理4证明边值问题（1）至少有1个正解.

2）t∈ ［0，1］，可知0≤u（t）≤ρ.由（H1）有

定理2 设0＜σ＜1，2＜α≤3，f∶［0，1）×［0，＋∞）→ ［0，＋∞）是连续的，且＋∞，（1－t）σf（t，y）在［0，1）×［0，＋∞）上连续.假设满足条件：① 存在1个连续非减函数φ∶［0，＋∞）→（0，＋∞），（t，ω）∈［0，1］×［0，＋∞），（1－t）σf（t，ω）≤φ（ω）；② 存在那么边值问题（1）存在1个正解.

［1］Lakshmikantham V，Leela S，Vasundhara J.Theory of Fractional Dynamic Systems［M］.Cambridge：Cambridge Academic Publishers，2009.

［2］同登科，王瑞和，杨河山.管内非 Newton流体分数阶流动的精确解［J］.中国科学 G辑，2005（3）：318－326.

［3］Delbosco D，Rodino L.Existence and uniqueness for a nonlinear fractional differential equation［J］.Math Anal Appl，1996，204：609－625.

［4］Zhang S Q.The existence of a positive solution for a nonlinear fractional differential equation［J］.Math Anal Appl，2000，252：804－812.

［5］Qiu Ting－ting，Bai Zhan－bing.Existence of positive solution for singular fractional differential equations［J］.Electronic Journal of Differential Equations，2008，146：1－9.

［6］Kilbas A A，Trujillo J J.Differential equations of fractional order：methods，results and problems I［J］.Applicable Analysis，2001，78：153－192.

［7］Kilbas A A，Marichev O I，Samko S G.Fractional Intergral and Derivatives：Theroy and Applications［M］.Switzerland：Gordon and Breach，1993.

［8］Zhang Shu－qin.Existence of positive solution for fractional differential equations with riemann－Liouville left－hand and right－hand fractional derivatives［J］.Electronic Journal of Differential Equations，2004，23：1－12.

［9］Krasnoselskii MA.Positive Solution of Operator Equation［M］.Groningen：Noordhoff，1964.

［10］Granas A，Guenther R B，Lee J W.Some general existence principle in the Caratheodory theory of nonlinear system［J］.Math Pure Appl，1991，70：153－196.

Existence of positive solution for a class of singular fractional differential equations

WANG Chun－lai，HOU Cheng－min＊
（DepartmentofMathematics，CollegeofScience，YanbianUniversity，Yanji133002，China）

We study the boundary value problem for a class of singular fractional differential equations.We first derive the Green’s function for the boundary value problem and sho wthat Green’s function satisfies some properties.Second，by using nonlinear alternative of Leray－Schauder type and Krasnoselskii’s fixed point theorem in a cone，some sufficient conditions of existence of at least one positive solution are established.

existence of positive solution；fractional differential equation；fixed point；cone

O175.6

A

1004－4353（2012）01－0001－06

2011－09－20

国家自然科学基金资助项目（11161049）

＊通信作者：侯成敏（1963—），女，教授，研究方向为微分方程理论及其应用.