贝叶斯推理主观性探析——对无差别原则和不变性的考察*1

程献礼，牛翠波

(1.南开大学 哲学院，天津 300071；2.华南师范大学 政治与行政学院，广东 广州 510631)

一、对贝叶斯原理的主观性质疑

“主观贝叶斯主义理论”，有时也被称为“归纳推理”或“归纳逻辑”，之所以称之为“主观的”，是因在贝叶斯定理运算中，它没有对先验概率的形式强加任何约束。因而贝叶斯阵营和非贝叶斯阵营的许多学者都认为，定理中的这种无约束不足以为归纳推理提供一个客观解释的目标假定，由于这些先验本身是“主观的”，而这种“主观性”被认为是与科学理念的客观性相悖的，因而也是站不住脚的。

笔者认为上述观点值得商榷。首先，存在于所有科学评估中的某种主观性质，是相关原理的一个优点，即，其使用是预先明确表示的而没有隐讳该观点。其次，该原理中实际掌握的是一套非常客观的“前提”，即先验概率的归纳推理逻辑。该逻辑与贝叶斯定理共同作为推理机，完全类似于作为“推理机”的演绎逻辑：筛选前提，产生有效的推论(即后验分布)。De Finetti(1972)指出：

根据该学说，我们努力做出尽可能不偏袒反映明智的判断，它表现了它们如何于何处干扰和暴露判断之间的可能不一致。“演绎”逻辑中存在启发性的分析使人确信：所接受的某些“确定”主观意见，蕴涵了其他意见的确定性，而主观概率理论，同样与不确定意见相关[1]。

但是这并不能证明不存在其他可接受的约束，实质上，这可能削弱或在某种情形下拒绝选择先验分布的自由度。的确，贝叶斯理论发展历程，在很大程度上是尝试寻求这类约束的过程。

本文将对贝叶斯推理中主观性质疑的无差别原理和不变性原理进行探讨。

二、无差别原则

凯恩斯所谓的“无差别原理”(The Principle of Indifference)[2]，在伯努利那里被称为“不充足理由律”(The Principle of Non-sufficient Reason)，有时也称之为“等概(率)原理”，是一种具有高度似合理性的对称原理，规定应通过相关对称的先验概率分布，如，掷一枚质地均匀的硬币，正面和反面出现的概率均为1/2，来考察划分成员间的对称关系。更准确地说，等分可能空间应该获得相对于零状态背景知识的同等概率。它不仅在直观上具有说服力，而且还具有极其重要的方法论影响力。托马斯·贝叶斯采用这条原则首次证明了统计推理中一个重要结论——所谓伯努利定理的“反演”[3]。

(一)J·伯努利的证明尝试

伯努利使用现代符号证明了由0和1的n次序列s组成的可能空间Ω，规定，其事件集合包含形式“在第i个指数上存在1”的所有事件(也能在随机变量语言中通过公式Xi-1进行描述，其中Xi是Ω上定义的n个{0，1}值随机变量)，而对“Xi=1”类事件指派客观概率的概率函数，与独立于i的概率p具有等概率，且事件“X1=x1”，…，“Xn=xn”，x=0或1，均是独立的。其结论是：任意小的ε>0(直至n)的相对频率(n-1)∑Xi与p差的绝对值的概率小于ε，随着n趋向无穷大，ε趋向于1[4]。

有些学者(包括伯努利本人)，希望把这种结果解释为对推理的许可，对于足够大的n，p接近观测到的相对频率，概率是非常大的，但这类许可的推论并不存在。伯努利定理通过真值参数p刻画概率分布的结果，因此p本身不是一个概率所依赖的随机变量。为了“反演”伯努利定理，要求定义更宽泛的概率空间Ω′，Ω′空间中命题类C，以及C上的概率函数P，p是一个随机变量，“p=r±δ”是C的一个事件。

(二)贝叶斯的证明尝试

伯努利定理的结论恰好是贝叶斯的证明尝试，并进一步给出了统计假说的后验分布。此处，p的取值被看成是关于如何实施该演算的一个主要概述的随机变量。实际上，它是似然性由函数nCrpr(1-p)n-r规定的贝叶斯定理的直接运用；而由无差别原则规定的p的先验概率，则是单位区间[0，1]上密度为1的均匀分布。故根据贝叶斯定理，该条件概率密度与f(p|r)=nCrpr(1-p)n-r成比例，但是由于f(p|r)是一个连续概率密度，它必须取整数1，因此，我们必然得出：

该密度是参数为r和n-r的β密度，明显趋近r/n的均值r+1/n+2.如图1所示。

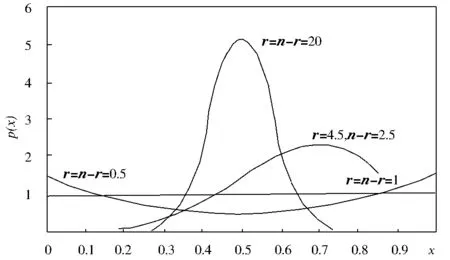
图1 β分布

该方差为(r+1)(n-r+1)/(n+2)2(n+3)；随着n的增大而接近于0，后验概率p是位于r/n周围并趋向于0的任意小区间。贝叶斯似乎解决了伯努利定理面临的问题：表明大样本p中，不仅包括Xi的可能结果，还包括二项式概率的可能值的扩展概率空间的随机变量，现在都显然近似等值于观测到的随机变量，是非常有可能的。应指出，这并非不是分析计算的、贝叶斯特有的推理方法，而是采用了几何构建的牛顿原理的方法。

(三)讨论

贝叶斯后验分布自身隐含着另一个假定前提——伯努利过程，但由于伯努利本人也假定了同样的情况，因此指责贝叶斯提出附加的模拟假定(modelling assumptions)是有失公允的。根据不充分理由原理，运用无差别原则来确定p的先验分布(伯努利本人也赞同这条原则)是一个重大创新。无论如何，在这个事例，以及在一个有界区间中取值的假定参数的任意其他事例中，无差别原则产生了一个完全确定的后验分布(当然还有一些其他分布)。

考察概率P(Xn-1=1/∑Xi=r)，其中这个和在1至n之间。根据条件概率法则，它等于比例P(Xi=r+1)/P(1/∑Xi=r)，这里第一个和等于n+1，第二个和等于n.运用上文中的推理，该比值等于：

(1)

它等于r+1/n+2.公式(1)即为“逐次法则”(Rule of Succession)。随着n增大，只要先前n次观测中有r次接近观察的相对频率r/n，下一观测的条件概率就将为1。故，不仅要调整下次抛掷正面朝上的信念度以适应观测到的正面朝上的相对频率，而且该结果还指出应如何调整。逐次法则同样很少投入到日常生活的应用之中。凯恩斯论述道：

逻辑方法中只有这个规则可以发挥如此惊人的作用。因为它从全然不知中证明了上帝的存在，并且用数值精度测量了太阳明天升起的概率[5]。

该法则作为普通枚举归纳的辩护，的确是根据过去已观测频率来调整任意未来事件的置信度的。在休谟看来，所有从过去观测的到将来预测的“可能论证”，都必然是循环的，这些论证都预设了它们打算要证明的论证内容。可是恰好相反，循环论证完全缺乏可替代论证之间的保证，而无差别原则更像是休谟怀疑论的答案。该问题在若干年后，豪森对休谟无法解决的归纳问题给出了全面论证[6]。

(四)辩护及其质疑

伴随着渐涨的质疑声及无差别原则所产生出明显相悖的结论，问题最终还是出现了。这里使用形式逻辑语言表述的现代例证在于表明，该潜在问题并非是由不精确定义产生的。用常见的现代逻辑符号表示的两种语言L1和L2，且包括等号(=)，通常，该符号在两种语言中均作为一个逻辑常项存在。设仅有一个谓词符号Q的语言L1和L2，其差异在于，L1具有分别以符号a和b表示的两个个体名词，而L2则没有。现在这两个命题显然能够通过各自语言中相同的形式命题进行符号化处理。

S1：至少存在一个具有Q的个体

S2：恰好存在两个个体

它们分别简单地表示为：

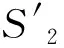
对该事例的标准解释为：作为任何无差别原则的应用基础，应选做更精细的区分的L1，而非粗糙的L2。然而，由于某种原因，这种辩护并未获得成功。首先，会惊奇地发现，一个具有个体名词的语言必然比没有个体名词的做了更为精确的区分，这种观点显然是不准确的；其次，这种异议规避了为什么应该选择更细划分的这一个问题；最后，反对意见声音最大的是，无差别原则为同等精细划分提供了不同的答案。

对于大样本，先验分布形式都不是特别重要；而对于随机大样本，参数的后验分布通常会在该参数最大似然估计的一个小区间内聚合，与先验分布的恰当形式无关。即便没有假定的均匀先验分布，贝叶斯二项式参数p的后验分布也会聚集在已观测相对频率(p的最大似然估计量)的小区间内。假如，已知结果是不确定的(非已知的)，那么，贝叶斯对使用无差别原则(虽然他并未如此称呼)的关切度就会降低。对于大多数问题，能享有大量数据，先验分布的形式会影响后验分布的形式。不管样本范围多大，贝叶斯都需要一个无偏见、无信息的先验。

无差别原则是一条对称性原则，它认为逻辑对称性应在无任何差异信息的前提下，反映在a先验概率的均匀分布之中。问题在连续空间中，对称性需要体现在均匀分布中，这就是逻辑的使命。无差别原则给予这个原理一种假定的身份，但历史上贝叶斯原理则以无差别原则为依据，并把它当做归纳推理的一个客观原理。没有这种授予，先验概率在后验分布演算中实际上是作为待定参数出现的。

三、贝叶斯主义对不变性的考察

不变性原则是具有直观吸引力的一种决策原理，即便是在经典统计学中也经常使用。其重要性不在于其自身，而在于它与包括费舍的“置信推断”[7]和Fraser的“结构推断”[8]等统计学提出的其他方法关系密切。以不变性方法为基础，产生了两个直观推论：有理不变性原则和不变性原理。前者是指在一个决策问题中，所采取的行为不应与所用的测量手段或其他随意发生的类似偶然事件有关；后者是指如果两个决策问题具有相同的形式结构，则在每一个问题中都应该采用同一个决策法则。对不变性的研究在选择合理的无信息先验时起着重要的作用，且以更多的观点来检验统计问题无疑是具有建设性的。

(一)Harold Jeffreys的证明方案

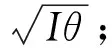
p(θ)=|dφ/dθ|p(φ)，

所以，规定指派先验密度的法则根据：p(θ)=Φ(θ).

对于某个函数项Φ(θ)，它是共变的，仅当它满足这个变换式的条件：

p(θ)=|dφ/dθ|Φ(φ).

(二)不变性的修正方案

尽管独立给出的一些先验分布受到极大的关注，产生的若干先验分布的Jeffreys规则不是唯一的共变法则，仍然存在一些诸如期望值的存在、该法则产生的先验分布之间都是所谓的不当分布(improper distribution)等技术性问题。不当分布在可能概率误差内(σ1的先验比例项近似地由柯西分布对数规定)，或通常只是作为易得的近似恰当分布而被引入的，只需在计算中进行合理关注，以使得计算保持总体上的一致。然而，与标准概率公理相矛盾可能说明该先验是演绎得出的，Jeffreys法则是一个特设性方法。

数学家Alfred Renyí和哲学家卡尔·波普尔(Karl Popper)在1945年至1955年间几乎各自同时提出：以原始条件概率函数的概率演算为基础，把条件概率当作初始概率，并修正适合不恰当分布原理。任何人，只要他们规定条件概率是有限的(即能够使它们正态化)，原则上能够在这里得到无界累积分布函数。无需置疑，这个发展成果具有相当大的吸引力，只是波普尔和Renyí的公理化方法一直没有被广泛采纳(或许更有理由采用Renyí的系统，这因为它在数学上最接近于标准的Kolmogorov原理，而且Renyí能够证明其条件函数表示为有限测度商所需的条件，也就是如何在标准形式体系中引进这些商)[10]。

虽然有多种控制不恰当分布的可接受方案，但采纳Jeffreys法则或其他不变法则的合理性仍未得到解决。任何人都会相信，选择任一法则，必须根据逻辑解释以证明这种选择的合理性，我们主张将这种选择作为公平赔率的一般条件加以证明。

无差别原则似乎具有这种类型的相关证明，但事实上该证明是前后矛盾的。Renyí本人给予了Jeffreys法则唯一的证明：在变换参数时缺少可论证的一致性，它能够表达独立可得的某些参数先验，特别是，满足不恰当分布的可接受性——分离地对于一个正态平均值和标准偏差(不是联合地，因为联合密度与σ2成比例，它不仅是其平均值和标准偏差的结果)，以及在较小范围内的一个二项式概率[9]。但是在其他各个方面，由于不变性属性缺少唯一性，它似乎是有欠缺的，而且这种态势没有得以扭转。

(三)Berger对不变性的研究

现当代贝叶斯主义学派领军人物之一美国统计学家Berger，首先以原子粒子衰变为例对不变性进行了分类，划分出“有理不变性原则”和“不变性原则”，认为在没有可用的先验信息的前提下，不变性原则就成为直观上和实践中都具有吸引力的方法，然后系统地阐述了不变性所需的概念和结构及其应用，如当样本大于1的统计问题，以及不变性和无信息先验不变性法则及其容许性。Berger论证了不变性方法和贝叶斯无信息先验方法实质上是等价的，且更倾向于后者；并认为，对具有建设性的不变性研究在选择合理的无信息先验时起着非常有用的作用[11]。

四、结语

首先，类似的普通观测通常也会削弱对客观先验的追求。其次，解释贝叶斯形式系统最自然的方式在于，该系统只是关于概率前提导出的概率推论的有效规则的集合。如果需要更精确的结论，那么就应做出(自己认为)更精确的假定，而研究工作的客观性，则存在于假定所刻画的结论的客观有效性之中。根据这种观点，许多人对“客观”先验分布的追求不仅是不必要的，而且是不合适的。这个结论被上述追求过程中产生的困境所强化，而且那些难题似乎只能通过使研究自我推翻的根本主观决策才可能被解决，甚至那些具有相同背景知识的人及追随Jaynes的专家们，仍然可以具有不同的观点。试图把多种意见变成单个统一意见，将被误解为强求一致的作风，将产生不利科学发展的推论。最后，抛弃相关信息，的确是不明智的做法，但这实际是为一些人所期待的。贝叶斯主义者告诉我们在何种情况下使用参照先验，或者为最简单的假说提供最高的先验概率；相反，概率公理表征的一致性约束如演绎逻辑的约束一样，都是严格的、非常客观的，而且在一个有效推理原理中，有效推理不仅和原来一样恰当，而且还恰到好处。

参考文献：

[1] Finetti B.de.Probability，Induction，and Statistics[M].New York：Wiley，1972：144.

[2] 章 詹.维特根斯坦的概率理论和“无差异原则”[D].上海：华东师范大学，2010:1.

[3] Bayes T.An Essay towards Solving a Problem in the Doctrine of Chances[J].Philosophical Transactions of the Royal Society，1958(53)：370-418.

[4] Howson C.and Urbach P.Scientific reasoning：the bayesian approach[M].3th edn，La Salle/Chicago：Open Court，1993：39-41.

[5] Keynes J M.A Treatise on probability [M].London：Macmillan，1921：89.

[6] Howson C.Hume’s Problem：Induction and the Justification of Belief[M].Oxford：Clarendon，2000.

[7] Fisher R A.Statistical test [J].Nature，1935(136)：474.

[8] David Brenner and D.A.S.Fraser.On foundations for conditional probability with statistical models-when is a class of functions a function[J].Statistical Papers，1979，20(3)：148-159.

[9] Jeffreys H.Theory of probability[M].Oxford：Clarendon，1961：182-184.

[10] Rényi A.On a New axiomatic theory of probability [J].Acta mathematica academiae scientiarum hungaricae，1955，6(3-4)：292-295.

[11] James O.Berger.统计决策论及贝叶斯分析:第二版[M].贾乃光，译.北京：中国统计出版社，1998：432-471.